Article contents
Riemann solution for a class of morphodynamic shallow water dam-break problems
Published online by Cambridge University Press: 29 November 2017
Abstract
This paper investigates a family of dam-break problems over an erodible bed. The hydrodynamics is described by the shallow water equations, and the bed change by a sediment-conservation equation, coupled to the hydrodynamics by a sediment transport (bed-load) law. When the initial states 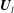 $\boldsymbol{U}_{l}$ and
$\boldsymbol{U}_{l}$ and 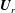 $\boldsymbol{U}_{r}$ are sufficiently close to each other the resulting solutions are consistent with the theory proposed by Lax (Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves, 1973, SIAM), that for a Riemann problem of
$\boldsymbol{U}_{r}$ are sufficiently close to each other the resulting solutions are consistent with the theory proposed by Lax (Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves, 1973, SIAM), that for a Riemann problem of  $n$ equations there are
$n$ equations there are  $n$ waves associated with the
$n$ waves associated with the  $n$ characteristic families. However, for wet–dry dam-break problems over a mobile bed, there are three governing equations, but only two waves. One wave vanishes because of the presence of the dry bed. When initial left and right bed levels (
$n$ characteristic families. However, for wet–dry dam-break problems over a mobile bed, there are three governing equations, but only two waves. One wave vanishes because of the presence of the dry bed. When initial left and right bed levels ( 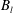 $B_{l}$ and
$B_{l}$ and 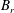 $B_{r}$ ) are far apart, it is shown that a semi-characteristic shock may occur, which happens because, unlike in shallow water flow on a fixed bed, the flux function is non-convex. In these circumstances it is shown that it is necessary to reconsider the usual shock conditions. Instead, we propose an implied internal shock structure the concept of which originates from the fact that the stationary shock over a fixed-bed discontinuity can be regarded as a limiting case of flow over a sloping fixed bed. The Needham & Hey (Phil. Trans. R. Soc. Lond. A, vol. 334, 1991, pp. 25–53) approximation for the ambiguous integral term
$B_{r}$ ) are far apart, it is shown that a semi-characteristic shock may occur, which happens because, unlike in shallow water flow on a fixed bed, the flux function is non-convex. In these circumstances it is shown that it is necessary to reconsider the usual shock conditions. Instead, we propose an implied internal shock structure the concept of which originates from the fact that the stationary shock over a fixed-bed discontinuity can be regarded as a limiting case of flow over a sloping fixed bed. The Needham & Hey (Phil. Trans. R. Soc. Lond. A, vol. 334, 1991, pp. 25–53) approximation for the ambiguous integral term 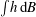 $\int \!h\,\text{d}B$ in the shock condition is improved based on this internal shock structure, such that mathematically valid solutions that incorporate a morphodynamic semi-characteristic shock are arrived at.
$\int \!h\,\text{d}B$ in the shock condition is improved based on this internal shock structure, such that mathematically valid solutions that incorporate a morphodynamic semi-characteristic shock are arrived at.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 3
- Cited by


