Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tokarev, Mikhail
Palkin, Egor
and
Mullyadzhanov, Rustam
2020.
Deep Reinforcement Learning Control of Cylinder Flow Using Rotary Oscillations at Low Reynolds Number.
Energies,
Vol. 13,
Issue. 22,
p.
5920.
Lai, Pengyu
Wang, Rui
Zhang, Wei
and
Xu, Hui
2021.
Parameter optimization of open-loop control of a circular cylinder by simplified reinforcement learning.
Physics of Fluids,
Vol. 33,
Issue. 10,
Zheng, Changdong
Ji, Tingwei
Xie, Fangfang
Zhang, Xinshuai
Zheng, Hongyu
and
Zheng, Yao
2021.
From active learning to deep reinforcement learning: Intelligent active flow control in suppressing vortex-induced vibration.
Physics of Fluids,
Vol. 33,
Issue. 6,
Uyeh, Daniel Dooyum
Bassey, Blessing Itoro
Mallipeddi, Rammohan
Asem-Hiablie, Senorpe
Amaizu, Maryleen
Woo, Seungmin
Ha, Yushin
and
Park, Tusan
2021.
A Reinforcement Learning Approach for Optimal Placement of Sensors in Protected Cultivation Systems.
IEEE Access,
Vol. 9,
Issue. ,
p.
100781.
Ren, Feng
Wang, Chenglei
and
Tang, Hui
2021.
Bluff body uses deep-reinforcement-learning trained active flow control to achieve hydrodynamic stealth.
Physics of Fluids,
Vol. 33,
Issue. 9,
Vona, Marco
and
Lauga, Eric
2021.
Stabilizing viscous extensional flows using reinforcement learning.
Physical Review E,
Vol. 104,
Issue. 5,
Morimoto, Masaki
Fukami, Kai
and
Fukagata, Koji
2021.
Experimental velocity data estimation for imperfect particle images using machine learning.
Physics of Fluids,
Vol. 33,
Issue. 8,
Castellanos, R.
Cornejo Maceda, G. Y.
de la Fuente, I.
Noack, B. R.
Ianiro, A.
and
Discetti, S.
2022.
Machine-learning flow control with few sensor feedback and measurement noise.
Physics of Fluids,
Vol. 34,
Issue. 4,
Jin, Bo
Illingworth, Simon J.
and
Sandberg, Richard D.
2022.
Optimal sensor and actuator placement for feedback control of vortex shedding.
Journal of Fluid Mechanics,
Vol. 932,
Issue. ,
Chen, Jiang-Li
Chen, Shao-Qiang
Ren, Feng
and
Hu, Hai-Bao
2022.
Artificially intelligent control of drag reduction around a circular cylinder based on wall pressure feedback.
Acta Physica Sinica,
Vol. 71,
Issue. 8,
p.
084701.
Wang, Yi-Zhe
Hua, Yue
Aubry, Nadine
Chen, Zhi-Hua
Wu, Wei-Tao
and
Cui, Jiahuan
2022.
Accelerating and improving deep reinforcement learning-based active flow control: Transfer training of policy network.
Physics of Fluids,
Vol. 34,
Issue. 7,
Passaggia, Pierre-Yves
Quansah, Asamaning
Mazellier, Nicolas
Maceda, Guy Y. Cornejo
and
Kourta, Azeddine
2022.
Real-time feedback stall control of an airfoil at large Reynolds numbers using linear genetic programming.
Physics of Fluids,
Vol. 34,
Issue. 4,
Kim, Junhyuk
Kim, Hyojin
Kim, Jiyeon
and
Lee, Changhoon
2022.
Deep reinforcement learning for large-eddy simulation modeling in wall-bounded turbulence.
Physics of Fluids,
Vol. 34,
Issue. 10,
Zeng, Kevin
Linot, Alec J.
and
Graham, Michael D.
2022.
Data-driven control of spatiotemporal chaos with reduced-order neural ODE-based models and reinforcement learning.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 478,
Issue. 2267,
Viquerat, J.
Meliga, P.
Larcher, A.
and
Hachem, E.
2022.
A review on deep reinforcement learning for fluid mechanics: An update.
Physics of Fluids,
Vol. 34,
Issue. 11,
Kurz, Marius
Offenhäuser, Philipp
Viola, Dominic
Shcherbakov, Oleksandr
Resch, Michael
and
Beck, Andrea
2022.
Deep reinforcement learning for computational fluid dynamics on HPC systems.
Journal of Computational Science,
Vol. 65,
Issue. ,
p.
101884.
Wang, Qiulei
Yan, Lei
Hu, Gang
Li, Chao
Xiao, Yiqing
Xiong, Hao
Rabault, Jean
and
Noack, Bernd R.
2022.
DRLinFluids: An open-source Python platform of coupling deep reinforcement learning and OpenFOAM.
Physics of Fluids,
Vol. 34,
Issue. 8,
Ghraieb, H.
Viquerat, J.
Larcher, A.
Meliga, P.
and
Hachem, E.
2022.
Single-step deep reinforcement learning for two- and three-dimensional optimal shape design.
AIP Advances,
Vol. 12,
Issue. 8,
Yamada, Keigo
Saito, Yuji
Nonomura, Taku
and
Asai, Keisuke
2022.
Greedy Sensor Selection for Weighted Linear Least Squares Estimation Under Correlated Noise.
IEEE Access,
Vol. 10,
Issue. ,
p.
79356.
Mao, Yiqian
Zhong, Shan
and
Yin, Hujun
2022.
Active flow control using deep reinforcement learning with time delays in Markov decision process and autoregressive policy.
Physics of Fluids,
Vol. 34,
Issue. 5,
 $18.4\,\%$ at a Reynolds number of
$18.4\,\%$ at a Reynolds number of  $120$ is obtained. This control policy is shown to be robust both to a Reynolds-number variation in the range
$120$ is obtained. This control policy is shown to be robust both to a Reynolds-number variation in the range  $[100;216]$ and to measurement noise, for signal-to-noise ratios as low as
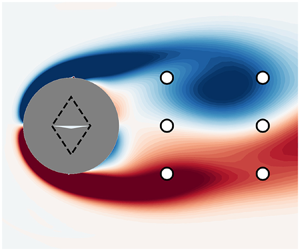
$[100;216]$ and to measurement noise, for signal-to-noise ratios as low as  $0.2$ with negligible impact on performance. Along with a systematic study on sensor number and location, the proposed sparsity-seeking algorithm has achieved a successful optimisation to a reduced five-sensor layout while keeping state-of-the-art performance. These results further highlight the interesting possibilities of reinforcement learning for active flow control and pave the way to efficient, robust and practical implementations of these control techniques in experimental or industrial systems.
$0.2$ with negligible impact on performance. Along with a systematic study on sensor number and location, the proposed sparsity-seeking algorithm has achieved a successful optimisation to a reduced five-sensor layout while keeping state-of-the-art performance. These results further highlight the interesting possibilities of reinforcement learning for active flow control and pave the way to efficient, robust and practical implementations of these control techniques in experimental or industrial systems.


