Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-29T10:50:00.123Z Has data issue: false hasContentIssue false
  • English
  • Français

The rotation of a sedimenting spheroidal particle in a linearly stratified fluid

Published online by Cambridge University Press:  24 December 2021

Arun Kumar Varanasi ,
Navaneeth K. Marath  and
Ganesh Subramanian Open the ORCID record for Ganesh Subramanian [Opens in a new window]
Arun Kumar Varanasi*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Center for Advanced Scientific Research, Bangalore560064, India
Navaneeth K. Marath*
Affiliation:
Mechanical Engineering, Indian Institute of Technology, Ropar140001, India
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Center for Advanced Scientific Research, Bangalore560064, India
*
†Email addresses for correspondence: arun.target@gmail.com, navaneeth@iitrpr.ac.in, sganesh@jncasr.ac.in
†Email addresses for correspondence: arun.target@gmail.com, navaneeth@iitrpr.ac.in, sganesh@jncasr.ac.in
†Email addresses for correspondence: arun.target@gmail.com, navaneeth@iitrpr.ac.in, sganesh@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

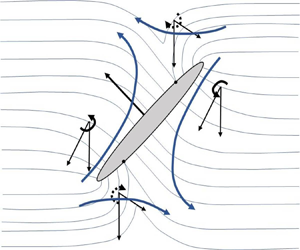
We derive analytically the angular velocity of a spheroid, of an arbitrary aspect ratio $\kappa$, sedimenting in a linearly stratified fluid. The analysis demarcates regions in parameter space corresponding to broadside-on and edgewise settling in the limit $Re, Ri_v \ll 1$, where $Re = \rho _0UL/\mu$ and $Ri_v =\gamma L^3\,g/\mu U$, the Reynolds and viscous Richardson numbers, respectively, are dimensionless measures of the importance of inertial and buoyancy forces relative to viscous ones. Here, $L$ is the spheroid semi-major axis, $U$ an appropriate settling velocity scale, $\mu$ the fluid viscosity and $\gamma \ (>0)$ the (constant) density gradient characterizing the stably stratified ambient, with the fluid density $\rho_0$ taken to be a constant within the Boussinesq framework. A reciprocal theorem formulation identifies three contributions to the angular velocity: (1) an $O(Re)$ inertial contribution that already exists in a homogeneous ambient, and orients the spheroid broadside-on; (2) an $O(Ri_v)$ hydrostatic contribution due to the ambient stratification that also orients the spheroid broadside-on; and (3) a hydrodynamic contribution arising from the perturbation of the ambient stratification whose nature depends on $Pe$; $Pe = UL/D$ being the Péclet number with $D$ the diffusivity of the stratifying agent. For $Pe \ll 1$, this contribution is $O(Ri_v)$ and orients prolate spheroids edgewise for all $\kappa \ (>1)$. For oblate spheroids, it changes sign across a critical aspect ratio $\kappa _c \approx 0.41$, orienting oblate spheroids with $\kappa _c < \kappa < 1$ edgewise and those with $\kappa < \kappa _c$ broadside-on. For $Pe \ll 1$, the hydrodynamic component is always smaller in magnitude than the hydrostatic one, so a sedimenting spheroid in this limit always orients broadside-on. For $Pe \gg 1$, the hydrodynamic contribution is dominant, being $O(Ri_v^{{2}/{3}}$) in the Stokes stratification regime characterized by $Re \ll Ri_v^{{1}/{3}}$, and orients the spheroid edgewise regardless of $\kappa$. Consideration of the inertial and large-$Pe$ stratification-induced angular velocities leads to two critical curves which separate the broadside-on and edgewise settling regimes in the $Ri_v/Re^{{3}/{2}}$–$\kappa$ plane, with the region between the curves corresponding to stable intermediate equilibrium orientations. The predictions for large $Pe$ are broadly consistent with observations.

JFM classification

Geophysical and Geological Flows: Stratified flows Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 933 , 25 February 2022 , A17
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anand, P., Ray, S.S. & Subramanian, G. 2020 Orientation dynamics of sedimenting anisotropic particles in turbulence. Phys. Rev. Lett. 125, 034501.CrossRefGoogle ScholarPubMed
Anis Alias, A.M. & Page, M.A. 2017 Low-Reynolds-number diffusion-driven flow around a horizontal cylinder. J. Fluid Mech. 825, 1035–1055.CrossRefGoogle Scholar
Ardekani, A.M. & Stocker, R. 2010 Stratlets: low Reynolds number point-force solutions in a stratified fluid. Phys. Rev. Lett. 105 (8), 084502.CrossRefGoogle Scholar
Auguste, F., Magnaudet, J. & Fabre, D. 2013 Falling styles of disks. J. Fluid Mech. 719, 388–405.CrossRefGoogle Scholar
Candelier, F., Mehaddi, R. & Vauquelin, O. 2014 The history force on a small particle in a linearly stratified fluid. J. Fluid Mech. 749, 184–200.CrossRefGoogle Scholar
Childress, S. 1964 The slow motion of a sphere in a rotating, viscous fluid. J. Fluid Mech. 20 (2), 305–314.CrossRefGoogle Scholar
Cole, M., Pennie, L., Halsband, C. & Galloway, T.S. 2011 Microplastics as contaminants in the marine environment: a review. Mar. Pollut. Bull. 62, 2588–2597.CrossRefGoogle ScholarPubMed
Dabade, V., Marath, N.K. & Subramanian, G. 2015 Effects of inertia and viscoelasticity on sedimenting anisotropic particles. J. Fluid Mech. 778, 133–188.CrossRefGoogle Scholar
Dabade, V., Marath, N.K. & Subramanian, G. 2016 The effect of inertia on the orientation dynamics of anisotropic particles in simple shear flow. J. Fluid Mech. 791, 631–703.CrossRefGoogle Scholar
Dandekar, R., Shaik, V.A. & Ardekani, A.M. 2020 Motion of an arbitrarily shaped particle in a density stratified fluid. J. Fluid Mech. 890, A16.CrossRefGoogle Scholar
Doostmohammadi, A. & Ardekani, A.M. 2013 Interaction between a pair of particles settling in a stratified fluid. Phys. Rev. E 88, 023029.CrossRefGoogle Scholar
Doostmohammadi, A. & Ardekani, A.M. 2014 Reorientation of elongated particles at density interfaces. Phys. Rev. E 90 (3), 033013.CrossRefGoogle ScholarPubMed
Doostmohammadi, A., Dabiri, S. & Ardekani, A.M. 2014 A numerical study of the dynamics of a particle settling at moderate Reynolds numbers in a linearly stratified fluid. J. Fluid Mech. 750, 5–32.CrossRefGoogle Scholar
Doostmohammadi, A., Stocker, R. & Ardekani, A.M. 2012 Low-Reynolds-number swimming at pycnoclines. Proc. Natl Acad. Sci. 109 (10), 3856–3861.CrossRefGoogle ScholarPubMed
Guillaume, M. & Magnaudet, J. 2002 Path instability of a rising bubble. Phys. Rev. Lett. 88 (1), 014502.Google Scholar
Gustavsson, K., Sheikh, M.Z., Lopez, D., Naso, A., Pumir, A. & Mehlig, B. 2019 Effect of fluid inertia on the orientation of a small prolate spheroid settling in turbulence. New J. Phys. 21, 083008.CrossRefGoogle Scholar
Hanazaki, H. 1988 A numerical study of three-dimensional stratified flow past a sphere. J. Fluid Mech. 192, 393–419.CrossRefGoogle Scholar
Hanazaki, H., Konishi, K. & Okamura, T. 2009 Schmidt-number effects on the flow past a sphere moving vertically in a stratified diffusive fluid. Phys. Fluids 21, 026602.CrossRefGoogle Scholar
Jiang, F., Zhao, L., Andersson, H.I., Gustavsson, K., Pumir, A. & Mehlig, B. 2014 Inertial torque on a small spheroid in a stationary uniform flow. Phys. Rev. Fluids 6, 024302.CrossRefGoogle Scholar
Jiang, F., Zhao, L., Andersson, H.I., Gustavsson, K., Pumir, A. & Mehlig, B. 2020 Inertial torque on a small spheroid in a stationary uniform flow. Phys. Rev. Fluids 6, 024302.CrossRefGoogle Scholar
Katija, K. & Dabiri, J.O. 2009 A viscosity-enhanced mechanism for biogenic ocean mixing. Nature 460 (7255), 624–626.CrossRefGoogle ScholarPubMed
Khayat, R.E. & Cox, R.G. 1989 Inertia effects on the motion of long slender bodies. J. Fluid Mech. 209, 435–462.CrossRefGoogle Scholar
Kim, S.J. & Karrila, S. 1991 Microhydrodynamics. Dover.Google Scholar
Kiorboe, T. 2011 How zooplankton feed: mechanisms, traits and trade-offs. Biol. Rev. 86, 311–339.CrossRefGoogle ScholarPubMed
Kunze, E., Dower, J.F., Beveridge, I., Dewey, R. & Bartlett, K.P. 2006 Observations of biologically generated turbulence in a coastal inlet. Science 313 (5794), 1768–1770.CrossRefGoogle Scholar
Kushch, V.I. 1997 Microstresses and effective elastic moduli of a solid reinforced by periodically distributed spheroidal particles. Intl J. Solids Struct. 34 (11), 1353–1366.CrossRefGoogle Scholar
Kushch, V.I. 1998 Elastic equilibrium of a medium containing a finite number of arbitrarily oriented spheroidal inclusions. Intl J. Solids Struct. 35 (12), 1187–1198.CrossRefGoogle Scholar
Lab, K. 2018 Phytoplankton Identification Guide 2018. Blurb.Google Scholar
Leal, L.G. 1992 Laminar Flow and Convective Transport Processes. Butterworth-Heinemann.Google Scholar
List, E.J. 1971 Laminar momentum jets in a stratified fluid. J. Fluid Mech. 45 (3), 561–574.CrossRefGoogle Scholar
Marath, N.K. & Subramanian, G. 2017 The effect of inertia on the time period of rotation on an anisotropic particle in simple shear flow. J. Fluid Mech. 830, 165–210.CrossRefGoogle Scholar
Mehaddi, R., Candelier, F. & Mehlig, B. 2018 Inertial drag on a sphere settling in a stratified fluid. J. Fluid Mech. 855, 1074–1087.CrossRefGoogle Scholar
Mercier, M.J., Wang, S., Péméja, J., Ern, P. & Ardekani, A.M. 2020 Settling disks in a linearly stratified fluid. J. Fluid Mech. 885, A2.CrossRefGoogle Scholar
Mrokowska, M.M. 2018 Stratification-induced reorientation of disk settling through ambient density transition. Sci. Rep. 8, 412.CrossRefGoogle ScholarPubMed
Mrokowska, M.M. 2020 a Dynamics of thin disk settling in two-layered fluid with density transition. Acta Geophys. 68, 1145–1160.CrossRefGoogle Scholar
Mrokowska, M.M. 2020 b Influence of pycnocline on settling behavior of non-spherical particle and wake evolution. Sci. Rep. 10, 20595.CrossRefGoogle ScholarPubMed
Munk, W.H. 1966 Abyssal recipes. Deep Sea Res. Oceanogr. Abstr. 13 (4), 707–730.CrossRefGoogle Scholar
Page, M.A. & Johnson, E.R. 2008 On steady linear diffusion-driven flow. J. Fluid Mech. 606, 433–443.CrossRefGoogle Scholar
Patricia, E., Frederic, R., DaAuguste, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.Google Scholar
Phillips, O.M. 1970 On flows induced by diffusion in a stably stratified fluid. Deep-Sea Res. 17, 435–443.Google Scholar
Prairie, J.C., Ziervogel, K., Camassa, R., Mclaughlin, R.M., White, B.L., Dewald, C. & Arnosti, C. 2015 Delayed settling of marine snow: effects of density gradient and particle properties, and implications for carbon cycling. Mar. Chem. 175, 28–38.CrossRefGoogle Scholar
Roberto, C., Claudia, F., Joyce, L., Mclaughlin, R.M. & Parker, R. 2009 Prolonged residence times for particles settling through stratified miscible fluids in the stokes regime. Phys. Fluids 21, 031702.Google Scholar
Saffman, P.G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (2), 385–400.CrossRefGoogle Scholar
Shaik, V.A. & Ardekani, A.M. 2020 Far-field flow and drift due to particles and organisms in density-stratified fluids. Phys. Rev. E 102, 063106.CrossRefGoogle ScholarPubMed
Srdic-Mitrovic, A.N., Mohamed, N.A. & Fernando, H.J.S. 1999 Gravitational settling of particles thruogh density interfaces. J. Fluid Mech. 381, 175–198.CrossRefGoogle Scholar
Subramanian, G. 2010 Viscosity-enhanced bio-mixing of the oceans. Curr. Sci. 98, 1103–1108.Google Scholar
Subramanian, G. & Koch, D.L. 2005 Inertial effects on fiber motion in simple shear flow. J. Fluid Mech. 535, 383–414.CrossRefGoogle Scholar
Turner, J.S. 1973 Buoyancy Effects of Fluids. Cambridge University Press.CrossRefGoogle Scholar
Turner, J.T. 2015 Zooplankton fecal pellets, marine snow, phytodetritus and the ocean's biological pump. Prog. Oceanogr. 130, 205–248.CrossRefGoogle Scholar
Turner, A. & Holmes, L. 2011 Occurrence, distribution and characteristics of beached plastic production pellets on the island of malta (central mediterranean). Mar. Pollut. Bull. 62, 377–381.CrossRefGoogle Scholar
Varanasi, A.K. & Subramanian, G. 2021 Motion of a sphere in a viscous stratified fluid. arXiv:2107.14422Google Scholar
Visser, A. 2007 Biomixing of the oceans? Science 316 (5826), 838–839.CrossRefGoogle ScholarPubMed
Wunsch, C. 1970 On oceanic boundary mixing. Deep-Sea Res. 17, 293–301.Google Scholar
Yick, K.Y., Torres, C.R., Peacock, T. & Stocker, R. 2009 Enhanced drag of a sphere settling in a stratified fluid at small Reynolds numbers. J. Fluid Mech. 632, 49–68.CrossRefGoogle Scholar
Zvirin, Y. & Chadwick, R.S. 1975 Settling of an axially symmetric body in a viscous stratified fluid. Intl J. Multiphase Flow 1, 743–752.CrossRefGoogle Scholar