Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T06:46:37.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Roughness receptivity and shielding in a flat plate boundary layer

Published online by Cambridge University Press:  20 July 2015

Matthew S. Kuester  and
Edward B. White
Matthew S. Kuester*
Affiliation:
Department of Aerospace and Ocean Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 20461, USA
Edward B. White
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: mkuester@vt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Surface roughness can affect boundary layer transition by acting as a receptivity mechanism for transient growth. While experiments have investigated transient growth of steady disturbances generated by discrete roughness elements, very few have studied distributed surface roughness. Some work predicts a ‘shielding’ effect, where smaller distributed roughness displaces the boundary layer away from the wall and lessens the impact of larger roughness peaks. This work describes an experiment specifically designed to study this effect. Three roughness configurations (a deterministic distributed roughness patch, a slanted rectangular prism, and the combination of the two) were manufactured using rapid prototyping and installed flush with the wall of a flat plate boundary layer. Naphthalene flow visualization and hotwire anemometry were used to characterize the boundary layer in the wakes of the different roughness configurations. Distributed roughness with roughness Reynolds numbers (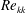$\mathit{Re}_{kk}$) between 113 and 182 initiated small-amplitude disturbances that underwent transient growth. The discrete roughness element created a pair of high- and low-speed steady streaks in the boundary layer at a sub-critical Reynolds number (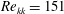$\mathit{Re}_{kk}=151$). At a higher Reynolds number (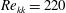$\mathit{Re}_{kk}=220$), the discrete element created a turbulent wedge 15 boundary layer thicknesses downstream. When the distributed roughness was added around the discrete roughness, the discrete element’s wake amplitude was decreased. For the higher Reynolds number, this provided a small but measurable transition delay. The distributed roughness redirects energy from longer spanwise wavelength modes to shorter spanwise wavelength modes. The presence of the distributed roughness also decreased the growth rate of secondary instabilities in the roughness wake. This work demonstrates that shielding can delay roughness-induced transition and lays the ground work for future studies of roughness-induced transition.

JFM classification

Boundary Layers: Boundary layer receptivity Boundary Layers: Boundary layer stability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 777 , 25 August 2015 , pp. 430 - 460
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11, 134.CrossRefGoogle Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. S. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.Google Scholar
Chu, J. & Goldstein, D.2012 Investigation of turbulent wedge spreading mechanism with comparison to turbulent spots. AIAA Paper 2012-0751.Google Scholar
Corke, T. C., Bar-Sever, A. & Morkovin, M. V. 1986 Experiments on transition enhancement by distributed roughness. Phys. Fluids 29 (10), 3199–3213.CrossRefGoogle Scholar
Cossu, C. & Brandt, L. 2002 Stabilization of Tollmien–Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 14 (8), L57–L60.Google Scholar
Denissen, N. A., Downs, R. S. III & White, E. B. 2009 Transient growth due to surface roughness: theory, simulation and experiment. AIAA Paper 2009-0175.Google Scholar
Denissen, N. A. & White, E. B. 2008 Roughness-induced bypass transition, revisited. AIAA J. 46 (7), 1874–1877.Google Scholar
Denissen, N. A. & White, E. B. 2013 Secondary instability of roughness-induced transient growth. Phys. Fluids 25 (11), 114108.Google Scholar
von Doenhoff, A. E. & Braslow, A. L. 1961 The effect of distributed surface roughness on laminar flow. In Boundary Layer and Flow Control, vol. 2, pp. 657–681.Google Scholar
Downs, R. S., White, E. B. & Denissen, N. A. 2008 Transient growth and transition induced by random distributed roughness. AIAA J. 46 (2), 451–462.Google Scholar
Drews, S. D.2012 Direct numerical simulation of flow past quasi-random distributed roughness. Master’s thesis, University of Texas at Austin, Austin, TX.Google Scholar
Drews, S. D., Downs, R. S. III, Doolittle, C. J., Goldstein, D. B. & White, E. B. 2011 Direct numerical simulations of flow past random distributed roughness. AIAA Paper 2011-0564.Google Scholar
Ergin, F. & White, E. 2006 Unsteady and transitional flows behind roughness elements. AIAA J. 44, 2504–2514.CrossRefGoogle Scholar
Fransson, J. H. M., Talamelli, A., Brandt, L. & Cossu, C. 2006 Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 96, 064501.CrossRefGoogle ScholarPubMed
Hunt, L. E., Downs, R. S. III, Kuester, M. S., White, E. B. & Saric, W. S. 2010 Flow quality measurements in the Klebanoff–Saric Wind Tunnel. AIAA Paper 2010-4538.Google Scholar
Kendall, J.1981 Laminar boundary layer velocity distortion by surface roughness: effect upon stability. AIAA Paper 1981-0195.CrossRefGoogle Scholar
Kuester, M. S. & White, E. B. 2014 Active noise control in a closed-circuit wind tunnel. AIAA J. 52 (9), 1829–1838.Google Scholar
Kurz, H. B. E. & Kloker, M. J. 2014 Receptivity of a swept-wing boundary layer to micron-sized discrete roughness elements. J. Fluid Mech. 755, 62–82.Google Scholar
Luchini, P. 2000 Reynolds-number-independent instability of the boundary layer over a flat surface: optimal perturbations. J. Fluid Mech. 404, 289–309.Google Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 2007 Numerical Recipes: The Art of Scientific Computing, 3rd edn. Cambridge University Press.Google Scholar
Reshotko, E. 2001 Transient growth: a factor in bypass transition. Phys. Fluids 13 (5), 1067–1075.CrossRefGoogle Scholar
Reshotko, E. & Leventhal, L.1981 Preliminary experimental study of disturbances in a laminar boundary-layer due to distributed roughness. AIAA Paper 1981-1224.CrossRefGoogle Scholar
Singh, K. & Lumley, J. L. 1971 Effect of roughness on the velocity profile of a laminar boundary layer. Appl. Sci. Res. 24 (1), 168–186.CrossRefGoogle Scholar
Smith, A. M. O. & Clutter, D. W. 1959 The smallest height of roughness capable of affecting boundary-layer transition. J. Aero. Sci. 26 (4), 229–245.Google Scholar
Stephani, K. A. & Goldstein, D. B.2009 DNS study of transient disturbance growth and bypass transition due to realistic roughness. AIAA Paper 2009-0585.CrossRefGoogle Scholar
Tani, I. 1969 Boundary-layer transition. Annu. Rev. Fluid Mech. 1 (1), 169–196.Google Scholar
Tumin, A. & Reshotko, E. 2001 Spatial theory of optimal disturbances in boundary layers. Phys. Fluids 13 (7), 2097–2104.Google Scholar
Tumin, A. & Reshotko, E. 2005 Receptivity of a boundary-layer flow to a three-dimensional hump at finite Reynolds numbers. Phys. Fluids 17 (9), 094101.CrossRefGoogle Scholar
White, E. B. 2002 Transient growth of stationary disturbances in a flat plate boundary layer. Phys. Fluids 14 (12), 4429–4439.Google Scholar
White, E. B. & Ergin, F. G. 2004 Using laminar-flow velocity profiles to locate the wall behind roughness elements. Exp. Fluids 36, 805–812.Google Scholar
White, E. B., Rice, J. M. & Ergin, F. G. 2005 Receptivity of stationary transient disturbances to surface roughness. Phys. Fluids 17 (6), 064109.CrossRefGoogle Scholar