Article contents
The sandpaper theory of flow–topography interaction for multilayer shallow-water systems
Published online by Cambridge University Press: 25 July 2024
Abstract
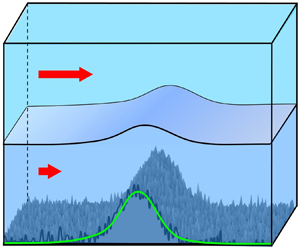
Seafloor roughness profoundly influences the pattern and dynamics of large-scale oceanic flows. However, these kilometre-scale topographic patterns are unresolved by global numerical Earth system models and will remain subgrid for the foreseeable future. To properly represent the effects of small-scale bathymetry in analytical and coarse-resolution numerical models, we develop the stratified ‘sandpaper’ theory of flow–topography interaction. This model, which is based on the multilayer shallow-water framework, extends its barotropic antecedent to stratified flows. The proposed theory is successfully tested on the configuration representing the interaction of a zonal current with a corrugated cross-flow ridge.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 2
- Cited by


