Article contents
Secondary instabilities of Görtler vortices in high-speed boundary layer flows
Published online by Cambridge University Press: 21 September 2015
Abstract
Görtler vortices developed in laminar boundary layer experience remarkable changes when the flow is subjected to compressibility effects. In the present study, five 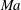 $\mathit{Ma}$ numbers, covering incompressible to hypersonic flows, at
$\mathit{Ma}$ numbers, covering incompressible to hypersonic flows, at 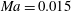 $\mathit{Ma}=0.015$, 1.5, 3.0, 4.5 and 6.0 are specified to illustrate these effects. Görtler vortices in subsonic and moderate supersonic flows (
$\mathit{Ma}=0.015$, 1.5, 3.0, 4.5 and 6.0 are specified to illustrate these effects. Görtler vortices in subsonic and moderate supersonic flows (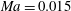 $\mathit{Ma}=0.015$, 1.5 and 3.0) are governed by the conventional wall-layer mode (mode W). In hypersonic flows (
$\mathit{Ma}=0.015$, 1.5 and 3.0) are governed by the conventional wall-layer mode (mode W). In hypersonic flows (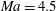 $\mathit{Ma}=4.5$, 6.0), the trapped-layer mode (mode T) becomes dominant. This difference is maintained and intensifies downstream leading to different scenarios of secondary instabilities. The linear and nonlinear development of Görtler vortices which are governed by dominant modal disturbances are investigated with direct marching of the nonlinear parabolic equations. The secondary instabilities of Görtler vortices set in when the resulting streaks are adequately developed. They are studied with Floquet theory at multiple streamwise locations. The secondary perturbations become unstable downstream following the sequence of sinuous mode type I, varicose mode and sinuous mode type II, indicating an increasing threshold amplitude. Onset conditions are determined for these modes. The above three modes can each have the largest growth rate under the right conditions. In the hypersonic cases, the threshold amplitude
$\mathit{Ma}=4.5$, 6.0), the trapped-layer mode (mode T) becomes dominant. This difference is maintained and intensifies downstream leading to different scenarios of secondary instabilities. The linear and nonlinear development of Görtler vortices which are governed by dominant modal disturbances are investigated with direct marching of the nonlinear parabolic equations. The secondary instabilities of Görtler vortices set in when the resulting streaks are adequately developed. They are studied with Floquet theory at multiple streamwise locations. The secondary perturbations become unstable downstream following the sequence of sinuous mode type I, varicose mode and sinuous mode type II, indicating an increasing threshold amplitude. Onset conditions are determined for these modes. The above three modes can each have the largest growth rate under the right conditions. In the hypersonic cases, the threshold amplitude 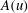 $A(u)$ is dramatically reduced, showing the significant impact of the thermal streaks. To investigate the parametric effect of the spanwise wavenumber, three global wavenumbers (
$A(u)$ is dramatically reduced, showing the significant impact of the thermal streaks. To investigate the parametric effect of the spanwise wavenumber, three global wavenumbers ( $B=0.5$, 1.0 and
$B=0.5$, 1.0 and 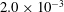 $2.0\times 10^{-3}$) are specified. The relationship between the dominant mode (sinuous or varicose) and the spanwise wavenumber of Görtler vortices found in incompressible flows (Li & Malik, J. Fluid Mech., vol. 297, 1995, pp. 77–100) is shown to be not fully applicable in high-speed cases. The sinuous mode becomes the most dangerous, regardless of the spanwise wavelength when
$2.0\times 10^{-3}$) are specified. The relationship between the dominant mode (sinuous or varicose) and the spanwise wavenumber of Görtler vortices found in incompressible flows (Li & Malik, J. Fluid Mech., vol. 297, 1995, pp. 77–100) is shown to be not fully applicable in high-speed cases. The sinuous mode becomes the most dangerous, regardless of the spanwise wavelength when 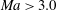 $\mathit{Ma}>3.0$. The subharmonic type can be the most dangerous mode while the detuned type can be neglected, although some of the sub-dominant secondary modes reach their peak growth rates under detuned states.
$\mathit{Ma}>3.0$. The subharmonic type can be the most dangerous mode while the detuned type can be neglected, although some of the sub-dominant secondary modes reach their peak growth rates under detuned states.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 81
- Cited by



