Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T05:31:45.245Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-destabilizing loop observed in a jetting-to-dripping transition

Published online by Cambridge University Press:  02 July 2014

Akira Umemura  and
Jun Osaka
Akira Umemura*
Affiliation:
Department of Aerospace Engineering, Nagoya University, Nagoya 464-8603, Japan
Jun Osaka
Affiliation:
Department of Aerospace Engineering, Nagoya University, Nagoya 464-8603, Japan
*
†Email address for correspondence: akira@nuae.nagoya-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that water slowly issued vertically downward exhibits a hysteresis phenomenon. A jetting-to-dripping transition appearing upon a stepwise decrease in jet issue speed was used to identify the origin of the Plateau–Rayleigh unstable wave elements which disintegrate the jetting liquid. In the present laboratory experiment using a stainless steel nozzle of inner radius 1 mm and length 30 mm, the transition occurred at a dimensionless jet issue speed of 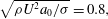$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\sqrt{\rho U^{2}a_{0} /\sigma } =0.8,$ where 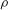$\rho $ and $\sigma $ respectively denote the density and surface tension coefficient of the liquid issued at the speed 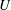$U$ from the nozzle of radius 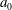$a_0$. The jet length gradually shortened with an oscillation of considerably large amplitude and period. High-speed camera images show that this oscillation is caused by tip contraction capillary wave (TCCW) elements which are elongated by the gravitationally accelerating jet flow and become Plateau–Rayleigh unstable wave elements. The jet length increases while the jet tip experiences end-pinching and radiates TCCW elements upstream. Only those TCCW elements destabilized at appropriate locations can grow sufficiently to shorten the jet. Since the unstable wave elements produced nearer the nozzle exit have much smaller amplitude at the jet tip, the end-pinching becomes effective. Thus, these processes are repeatable and constitute a self-destabilizing loop. The observed jetting-to-dripping transition has nothing to do with the random nozzle disturbances which were believed to be the origin of the Plateau–Rayleigh unstable wave in conventional instability theories. It is also different from the feature conjectured from current absolute/convective instability analysis. The underling physics of the self-destabilizing loop are explored in detail by numerical simulations based on a one-dimensional model.

JFM classification

Waves/Free-surface Flows: Capillary waves Instability: Instability Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 184 - 218
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amagai, K. 2000 Instability theory of circular liquid jet. Atomization 9, 261–269 (in Japanese).Google Scholar
Anna, S. L., Bontoux, N. & Stone, H. A. 2003 Formation of dispersions using flow focusing in microchannels. Appl. Phys. Lett. 82, 364–366.Google Scholar
Ashgriz, N. & Mashayek, F. 1995 Temporal analysis of capillary jet breakup. J. Fluid Mech. 291, 163–190.Google Scholar
Bachelor, G. K. 1958 Collected Works of G.I. Taylor. Cambridge University Press.Google Scholar
Blasisot, J. B. & Adeline, S. 2003 Instabilities on a free falling jet under an internal flow breakup mode regime. Intl J. Multiphase Flow 29, 629–653.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon.Google Scholar
Clanet, C. & Lasheras, J. C. 1999 Transition from dripping to jetting. J. Fluid Mech. 383, 307–326.Google Scholar
Coullet, P., Mahadevan, L. & Riera, C. S. 2005 Hydrodynamical models for the chaotic dripping faucet. J. Fluid Mech. 526, 1–17.CrossRefGoogle Scholar
Debler, W. & Yu, D. 1988 The breakup of laminar liquid jets. Proc. R. Soc. Lond. A 415, 107–110.Google Scholar
Eggers, J. 1997 Nonlinear dynamics and breakup of free surface flows. Rev. Mod. Phys. 69, 865–930.Google Scholar
Eggers, J. & Dupont, T. F. 1994 Drop formation in a one-dimensional approximation of the Navier–Stokes equation. J. Fluid Mech. 262, 205–221.CrossRefGoogle Scholar
Eggers, J. & Villermaux, E. 2008 Physics of liquid jets. Rep. Prog. Phys. 71, 036601.Google Scholar
Fargie, D. & Martin, B. W. 1971 Developing laminar flow in a pipe of circular cross-section. Proc. R. Soc. Lond. A 321, 461–476.Google Scholar
Fenn, R. W. & Middleman, S. 1969 Newtonian jet stability: the role of air resistance. AIChE J. 12, 379–383.Google Scholar
Gañán-Calvo, A. M. 1998 Generation of steady liquid microthreds and micro-sized monodisperse sprays in a gas stream. Phys. Rev. Lett. 80, 285–288.Google Scholar
Gordillo, J. M. & Gekle, S. 2010 Generation and breakup of Worthington jets after cavity collapse. Part 2. Tip breakup of stretched jets. J. Fluid Mech. 663, 331–346.CrossRefGoogle Scholar
Gordillo, J. M. & Pérez-Saborid, M. 2005 Aerodynamic effects in the breakup of liquid jets: on the first wind-induced breakup regime. J. Fluid Mech. 541, 1–20.Google Scholar
Gorokhovski, M. & Hermmann, M. 2008 Modeling primary atomization. Annu. Rev. Fluid Mech. 40, 343–366.CrossRefGoogle Scholar
Grant, R. P. & Middleman, S. 1966 Newtonian jet stability. AIChE J. 12, 678–869.Google Scholar
Guillot, P., Colin, A., Utada, A. S. & Adjdari, A. 2007 Stability of a jet in confined pressure-driven biphasic flows at low Reynolds number. Phys. Rev. Lett. 99, 104502.Google Scholar
Hiroyasu, H., Arai, M. & Shimizu, M.1991 Break-up length of a liquid jet and internal flow in a nozzle, ICLASS-91, Gaithersburg, MD, pp. 275–282.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Mech. 22, 473–537.Google Scholar
Ibrahim, E. A. & Marshal, S. O. 2000 Istability of a liquid jet of parabolic velocity profile. Chem. Engng J. 76, 17–21.Google Scholar
Karasawa, T., Tanaka, M., Abe, K., Shiga, S. & Kurabayashi, T. 1992 Effect of nozzle configuration on the atomization of a steady spray. Atomiz. Sprays 2, 411–426.Google Scholar
Keller, J. B., Ubinow, S. L. & Tu, Y. O. 1973 Spatial instability of a jet. Phys. Fluids 16, 2052–2055.Google Scholar
Lasheras, J. C. & Hopfinger, E. J. 2000 Liquid jet instability and atomization in a coaxial gas stream. Annu. Rev. Fluid Mech. 32, 275–308.CrossRefGoogle Scholar
Le Dizes, S. 1997 Global modes in falling capillary jets. Eur. J. Mech. (B/Fluids) 16, 166–182.Google Scholar
Leib, S. J. & Goldstein, M. E. 1986 The generation of capillary instabilities on a liquid jet. J. Fluid Mech. 168, 479–500.Google Scholar
Leroux, S., Dumouchel, C. & Ledoux, M. 1997 The breakup length of laminar cylindrical jets: modification of Weber’s theory. Intl J. Fluid Mech. Res. 24, 428–438.Google Scholar
Lin, S. P. 2003 Breakup of Liquid Sheets and Jets. Cambridge University Press.Google Scholar
Lin, S. P. & Lian, Z. W. 1989 Absolute instability of a liquid jet in a gas. Phys. Fluids A 1, 490–493.Google Scholar
Lin, S. P. & Reitz, R. D. 1998 Drop and spray formation from a liquid jet. Annu. Rev. Fluid Mech. 30, 85–105.Google Scholar
Marmottan, P. & Villermaux, E. 2004 On spray formation. J. Fluid Mech. 498, 73–111.CrossRefGoogle Scholar
Mayer, E. 1961 Theory of liquid atomization in high velocity gas stream. Am. Rocket Soc. J. 31, 1783–1785.Google Scholar
McCarthy, M. J. & Molloy, N. A. 1974 Review of stability of liquid jets and influence of nozzle design. Chem. Engng J. 7, 1–20.Google Scholar
Meister, B. J. & Scheele, G. F. 1967 General solution of the Tomotika stability analysis for a cylindrical jet. AIChE J. 13, 682–688.Google Scholar
Monkewitz, P. A. 1990 The role of absolute and convective instability in predicting the behavior of fluid systems. Eur. J. Mech. (B/Fluids) 9, 395–413.Google Scholar
Monkewitz, P. A., Davis, J., Bojorquez, B. & Yu, M. H. 1988 The breakup of a liquid jet at high Weber number. Bull. Am. Phys. Soc. 33, 2273.Google Scholar
Nelson, P., Power, T. & Seffert, U. 1995 Dynamic theory of pearling instability in cylindrical vesicles. Phys. Rev. Lett. 74, 3384–3387.Google Scholar
O’Donnell, B., Chen, J. N. & Lin, S. P. 2001 Transition from convective to absolute instability in a liquid jet. Phys. Fluids 13, 2732–2734.CrossRefGoogle Scholar
Pan, Y. & Suga, K. 2006 A numerical study on the breakup process of laminar liquid jets into a gas. Phys. Fluids 18, 052101.Google Scholar
Phinney, R. E. & Humphries, W. 1973 Stability of a laminar jet of viscous liquid-influence of nozzle shape. AIChE J. 19, 655–657.CrossRefGoogle Scholar
Plateau, J. 1873 Statique Experimentale et Theorique des Liquides Soumis aux Seules Forces Moleculaires, vol. 2. Gauthier-Villars.Google Scholar
Power, T. R. & Goldstein, R. E. 1997 Pearling and pinching: propagation of Rayleigh instabilities. Phys. Rev. Lett. 78, 2555–2558.Google Scholar
Rayleigh, L. 1878 On the Instability of Jets. Proc. Lond. Math. Soc. 10, 4–13.Google Scholar
Reitz, R. D. & Bracco, F. V. 1986 Mechanisms of breakup of round liquid jets. In The Encyclopedia of Fluid Mechanics (ed. Cheremisnoff, N.), vol. 3, pp. 233–249. Gulf.Google Scholar
Rubio-Rubio, M., Sevilla, A. & Gordillo, J. M. 2013 On the thinnest steady threds obtained by gravitational stretching of capillary jets. J. Fluid Mech. 729, 471–483.CrossRefGoogle Scholar
Schulkes, R. M. S. M. 1996 The contraction of liquid filaments. J. Fluid Mech. 309, 277–300.Google Scholar
Shinjo, J. & Umemura, A. 2010 Simulation of liquid jet primary breakup: dynamics of ligament and droplet formation. Intl J. Multiphase Flow 36, 513–532.Google Scholar
Shinjo, J. & Umemura, A. 2011 Detailed simulation of primary atomization mechanism in diesel jet spray (isolated identification of liquid jet tip effects). Proc. Combust. Inst. 33, 2089–2097.Google Scholar
Smith, S. W. & Moss, H. 1917 Experiments with mercury jets. Proc. R. Soc. Lond. A 43, 373–393.Google Scholar
Sparrow, E. M., Lin, S. H. & Lindgren, T. S. 1964 Flow development in the hydrodynamic entrance region of tubes and ducts. Phys. Fluids 7, 338–347.Google Scholar
Sterling, A. M. & Sleicher, C. A. 1975 The instability of capillary jets. J. Fluid Mech. 68, 477–495.Google Scholar
Stone, H. A. & Leal, L. G. 1989 Relaxation and breakup of an initially extended drop in an otherwise quiescent fluid. J. Fluid Mech. 198, 399–427.Google Scholar
Taylor, G. I. 1959 The dynamics of thin sheets of fluid. III disintegration of fluid sheets. Proc. R. Soc. Lond. A 253, 313–321.Google Scholar
Tomotika, J. 1955 On the instability of a cylindrical thread of a viscous liquid surrounded by another viscous fluid. Proc. R. Soc. Lond. 150, 322–337.Google Scholar
Tyler, E. & Richardson, E. G. 1925 The characterisitic curves of liquid jets. Proc. R. Soc. Lond. A 37, 297–311.Google Scholar
Tyler, E. & Watkin, F. 1932 Experiments with capillary jets. Phil. Mag. 14, 849–881.Google Scholar
Umemura, A. 2011 Self-destabilizing mechanism of a liquid jet issuing from a long nozzle. Phys. Rev. E 83, 046307.Google Scholar
Umemura, A., Kawanabe, S., Suzuki, S. & Osaka, J. 2011 Two-valued breakup length of a water jet issuing from a finite-length nozzle under normal gravity. Phys. Rev. E 84, 036309.Google Scholar
Vihinen, I., Honohan, A. M. & Lin, S. P. 1997 Image of absolute instability in a liquid jet. Phys. Fluids 9, 3117–3119.Google Scholar
Weber, C. 1931 Zum Zerfall eines Flüssingkeitsstrahles. Z. Angew. Math. Mech. 11, 136–145.Google Scholar
Wu, P. K., Miranda, R. F. & Faeth, G. M. 1995 Effect of initial flow conditions on primary breakup of non-turbulent and turbulent round liquid jets. Atomiz. Sprays 5, 175–196.Google Scholar
Yecko, P., Zaleski, S. & Fullana, J. M. 2002 Viscous modes in two-phase mixing layers. Phys. Fluids 14, 4115–4122.Google Scholar
Yecko, P. & Zaleski, S. 2005 Transient growth in two-phase mixing layers. J. Fluid Mech. 528, 43–52.Google Scholar