Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T06:43:21.180Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-preservation in a zero pressure gradient rough-wall turbulent boundary layer

Published online by Cambridge University Press:  22 December 2015

K. M. Talluru ,
L. Djenidi ,
Md. Kamruzzaman  and
R. A. Antonia
K. M. Talluru*
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
L. Djenidi
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
Md. Kamruzzaman
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
R. A. Antonia
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
*
†Email address for correspondence: murali.talluru@newcastle.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

A self-preservation (SP) analysis is carried out for a zero pressure gradient (ZPG) rough-wall turbulent boundary layer with a view to establishing the requirements of complete SP (i.e. SP across the entire layer) and determining if these are achievable. The analysis shows that SP is achievable in certain rough-wall boundary layers (irrespectively of the Reynolds number 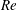$Re$), when the mean viscous stress is zero or negligible compared to the form drag across the entire boundary layer. In this case, the velocity scale 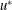$u^{\ast }$ must be constant, the length scale 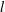$l$ should vary linearly with the streamwise distance $x$ and the roughness height 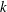$k$ must be proportional to 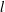$l$. Although this result is consistent with that of Rotta (Prog. Aeronaut. Sci., vol. 2 (1), 1962, pp. 1–95), it is derived in a more rigorous manner than the method employed by Rotta. Further, it is noted that complete SP is not possible in a smooth-wall ZPG turbulent boundary layer. The SP conditions are tested against published experimental data on both a smooth wall (Kulandaivelu, 2012, PhD thesis, The University of Melbourne) and a rough wall, where the roughness height increases linearly with $x$ (Kameda et al., J. Fluid Sci. Technol., vol. 3 (1), 2008, pp. 31–42). Complete SP in a ZPG rough-wall turbulent boundary layer seems indeed possible when 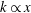$k\propto x$.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 57 - 69
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barenblatt, G. I. 1993 Scaling laws for fully developed turbulent shear flows. Part 1. Basic hypotheses and analysis. J. Fluid Mech. 248, 513–520.CrossRefGoogle Scholar
Barenblatt, G. I. 1996 Scaling, Self-Similarity, and Intermediate Asymptotics. Cambridge University Press.CrossRefGoogle Scholar
Blasius, H. 1908 Grenzschichten in Flussigkeiten mit kleiner Reibung. Z. Math. Phys. 56, 1–37.Google Scholar
Chauhan, K. A., Nagib, H. M. & Monkewitz, P. A. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.Google Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aero. Sci. 21 (2), 91–108.CrossRefGoogle Scholar
Clauser, F. H. 1956 The turbulent boundary layer. Adv. Appl. Mech. 4, 1–51.CrossRefGoogle Scholar
Coles, D. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1 (02), 191–226.CrossRefGoogle Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.CrossRefGoogle Scholar
Finnigan, J. J. 1985 Turbulent transport in flexible plant canopies. In The Forest-Atmosphere Interaction, pp. 443–480. Springer.CrossRefGoogle Scholar
George, W. K. 1995 Some new ideas for similarity of turbulent shear flows. Turbul. Heat Mass Transfer 1, 13–24.Google Scholar
George, W. K. & Castillo, L. 1997 Zero-pressure-gradient turbulent boundary layer. Appl. Mech. Rev. 50 (12), 689–729.CrossRefGoogle Scholar
Gad-el Hak, M. & Bandyopadhyay, P. R. 1994 Reynolds number effects in wall-bounded turbulent flows. Appl. Mech. Rev. 47 (8), 307–365.CrossRefGoogle Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.CrossRefGoogle Scholar
Jones, M. B., Nickels, T. B. & Marusic, I. 2008 On the asymptotic similarity of the zero-pressure-gradient turbulent boundary layer. J. Fluid Mech. 616, 195–203.CrossRefGoogle Scholar
Kameda, T., Mochizuki, S., Osaka, H. & Higaki, K. 2008 Realization of the turbulent boundary layer over the rough wall satisfied the conditions of complete similarity and its mean flow quantities. J. Fluid Sci. Technol. 3 (1), 31–42.CrossRefGoogle Scholar
Kamruzzaman, Md., Djenidi, L., Antonia, R. A. & Talluru, K. M. 2015 Drag of a turbulent boundary layer with transverse 2d circular rods on the wall. Exp. Fluids 56 (6), 1–8.CrossRefGoogle Scholar
Kulandaivelu, V.2012 Evolution of zero pressure gradient turbulent boundary layers from different initial conditions. PhD thesis, The University of Melbourne.Google Scholar
Lee, S. H. & Sung, H. J. 2007 Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J. Fluid Mech. 584, 125–146.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.CrossRefGoogle Scholar
Mellor, G. L. & Gibson, D. M. 1966 Equilibrium turbulent boundary layers. J. Fluid Mech. 24, 225–253.CrossRefGoogle Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.CrossRefGoogle Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aeronaut. Sci. 2 (1), 1–95.CrossRefGoogle Scholar
Schlichting, H. 1979 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Smalley, R. J., Antonia, R. A. & Djenidi, L. 2001 Self-preservation of rough-wall turbulent boundary layers. Eur. J. Mech. (B/Fluids) 20 (5), 591–602.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.CrossRefGoogle Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Weyburne, D. W.2008 The mathematics of flow similarity of the velocity boundary layer. Tech. Rep. AFRL-RY-HS-TR-2010-0014. Air Force Research Laboratory.CrossRefGoogle Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar