Published online by Cambridge University Press: 04 May 2017
We investigate fully developed turbulence in stratified plane Couette flows using direct numerical simulations similar to those reported by Deusebio et al. (J. Fluid Mech., vol. 781, 2015, pp. 298–329) expanding the range of Prandtl number 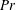 $Pr$ examined by two orders of magnitude from 0.7 up to 70. Significant effects of
$Pr$ examined by two orders of magnitude from 0.7 up to 70. Significant effects of 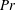 $Pr$ on the heat and momentum fluxes across the channel gap and on the mean temperature and velocity profile are observed. These effects can be described through a mixing length model coupling Monin–Obukhov (M–O) similarity theory and van Driest damping functions. We then employ M–O theory to formulate similarity scalings for various flow diagnostics for the stratified turbulence in the gap interior. The midchannel gap gradient Richardson number
$Pr$ on the heat and momentum fluxes across the channel gap and on the mean temperature and velocity profile are observed. These effects can be described through a mixing length model coupling Monin–Obukhov (M–O) similarity theory and van Driest damping functions. We then employ M–O theory to formulate similarity scalings for various flow diagnostics for the stratified turbulence in the gap interior. The midchannel gap gradient Richardson number 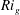 $Ri_{g}$ is determined by the length scale ratio
$Ri_{g}$ is determined by the length scale ratio 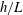 $h/L$, where
$h/L$, where 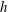 $h$ is the half-channel gap depth and
$h$ is the half-channel gap depth and 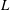 $L$ is the Obukhov length scale. As
$L$ is the Obukhov length scale. As 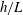 $h/L$ approaches very large values,
$h/L$ approaches very large values, 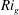 $Ri_{g}$ asymptotes to a maximum characteristic value of approximately 0.2. The buoyancy Reynolds number
$Ri_{g}$ asymptotes to a maximum characteristic value of approximately 0.2. The buoyancy Reynolds number 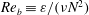 $Re_{b}\equiv \unicode[STIX]{x1D700}/(\unicode[STIX]{x1D708}N^{2})$, where
$Re_{b}\equiv \unicode[STIX]{x1D700}/(\unicode[STIX]{x1D708}N^{2})$, where  $\unicode[STIX]{x1D700}$ is the dissipation,
$\unicode[STIX]{x1D700}$ is the dissipation,  $\unicode[STIX]{x1D708}$ is the kinematic viscosity and
$\unicode[STIX]{x1D708}$ is the kinematic viscosity and 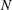 $N$ is the buoyancy frequency defined in terms of the local mean density gradient, scales linearly with the length scale ratio
$N$ is the buoyancy frequency defined in terms of the local mean density gradient, scales linearly with the length scale ratio 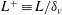 $L^{+}\equiv L/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$, where
$L^{+}\equiv L/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$, where 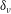 $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$ is the near-wall viscous scale. The flux Richardson number
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$ is the near-wall viscous scale. The flux Richardson number 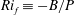 $Ri_{f}\equiv -B/P$, where
$Ri_{f}\equiv -B/P$, where 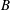 $B$ is the buoyancy flux and
$B$ is the buoyancy flux and 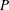 $P$ is the shear production, is found to be proportional to
$P$ is the shear production, is found to be proportional to 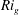 $Ri_{g}$. This then leads to a turbulent Prandtl number
$Ri_{g}$. This then leads to a turbulent Prandtl number 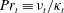 $Pr_{t}\equiv \unicode[STIX]{x1D708}_{t}/\unicode[STIX]{x1D705}_{t}$ of order unity, where
$Pr_{t}\equiv \unicode[STIX]{x1D708}_{t}/\unicode[STIX]{x1D705}_{t}$ of order unity, where 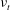 $\unicode[STIX]{x1D708}_{t}$ and
$\unicode[STIX]{x1D708}_{t}$ and 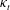 $\unicode[STIX]{x1D705}_{t}$ are the turbulent viscosity and diffusivity respectively, which is consistent with Reynolds analogy. The turbulent Froude number
$\unicode[STIX]{x1D705}_{t}$ are the turbulent viscosity and diffusivity respectively, which is consistent with Reynolds analogy. The turbulent Froude number 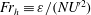 $Fr_{h}\equiv \unicode[STIX]{x1D700}/(NU^{\prime 2})$, where
$Fr_{h}\equiv \unicode[STIX]{x1D700}/(NU^{\prime 2})$, where 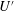 $U^{\prime }$ is a turbulent horizontal velocity scale, is found to vary like
$U^{\prime }$ is a turbulent horizontal velocity scale, is found to vary like 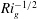 $Ri_{g}^{-1/2}$. All these scalings are consistent with our numerical data and appear to be independent of
$Ri_{g}^{-1/2}$. All these scalings are consistent with our numerical data and appear to be independent of 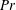 $Pr$. The classical Osborn model based on turbulent kinetic energy balance in statistically stationary stratified sheared turbulence (Osborn, J. Phys. Oceanogr., vol. 10, 1980, pp. 83–89), together with M–O scalings, results in a parameterization of
$Pr$. The classical Osborn model based on turbulent kinetic energy balance in statistically stationary stratified sheared turbulence (Osborn, J. Phys. Oceanogr., vol. 10, 1980, pp. 83–89), together with M–O scalings, results in a parameterization of 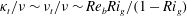 $\unicode[STIX]{x1D705}_{t}/\unicode[STIX]{x1D708}\sim \unicode[STIX]{x1D708}_{t}/\unicode[STIX]{x1D708}\sim Re_{b}Ri_{g}/(1-Ri_{g})$. With this parameterization validated through direct numerical simulation data, we provide physical interpretations of these results in the context of M–O similarity theory. These results are also discussed and rationalized with respect to other parameterizations in the literature. This paper demonstrates the role of M–O similarity in setting the mixing efficiency of equilibrated constant-flux layers, and the effects of Prandtl number on mixing in wall-bounded stratified turbulent flows.
$\unicode[STIX]{x1D705}_{t}/\unicode[STIX]{x1D708}\sim \unicode[STIX]{x1D708}_{t}/\unicode[STIX]{x1D708}\sim Re_{b}Ri_{g}/(1-Ri_{g})$. With this parameterization validated through direct numerical simulation data, we provide physical interpretations of these results in the context of M–O similarity theory. These results are also discussed and rationalized with respect to other parameterizations in the literature. This paper demonstrates the role of M–O similarity in setting the mixing efficiency of equilibrated constant-flux layers, and the effects of Prandtl number on mixing in wall-bounded stratified turbulent flows.