Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T07:22:26.922Z Has data issue: false hasContentIssue false
  • English
  • Français

A self-sustaining process theory for uniform momentum zones and internal shear layers in high Reynolds number shear flows

Published online by Cambridge University Press:  02 September 2020

Brandon Montemuro Open the ORCID record for Brandon Montemuro [Opens in a new window] ,
Christopher M. White Open the ORCID record for Christopher M. White [Opens in a new window] ,
Joseph C. Klewicki Open the ORCID record for Joseph C. Klewicki [Opens in a new window]  and
Gregory P. Chini Open the ORCID record for Gregory P. Chini [Opens in a new window]
Brandon Montemuro
Affiliation:
Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH03824, USA
Christopher M. White
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH03824, USA
Joseph C. Klewicki
Affiliation:
Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH03824, USA Department of Mechanical Engineering, University of New Hampshire, Durham, NH03824, USA Department of Mechanical Engineering, University of Melbourne, Melbourne, Victoria3010, Australia
Gregory P. Chini*
Affiliation:
Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH03824, USA Department of Mechanical Engineering, University of New Hampshire, Durham, NH03824, USA
*
†Email address for correspondence: greg.chini@unh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

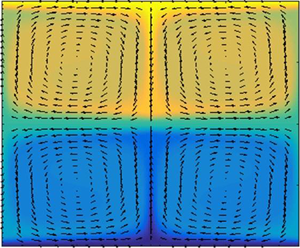
Many exact coherent states (ECS) arising in wall-bounded shear flows have an asymptotic structure at extreme Reynolds number $Re$ in which the effective Reynolds number governing the streak and roll dynamics is $\mathit {O}(1)$. Consequently, these viscous ECS are not suitable candidates for quasi-coherent structures away from the wall that necessarily are inviscid in the mean. Specifically, viscous ECS cannot account for the singular nature of the inertial domain, where the flow self-organizes into uniform momentum zones (UMZs) separated by internal shear layers and the instantaneous streamwise velocity develops a staircase-like profile. In this investigation, a large-$Re$ asymptotic analysis is performed to explore the potential for a three-dimensional, short streamwise- and spanwise-wavelength instability of the embedded shear layers to sustain a spatially distributed array of much larger-scale, effectively inviscid streamwise roll motions. In contrast to other self-sustaining process theories, the rolls are sufficiently strong to differentially homogenize the background shear flow, thereby providing a mechanistic explanation for the formation and maintenance of UMZs and interlaced shear layers that respects the leading-order balance structure of the mean dynamics.

JFM classification

Turbulent Flows: Turbulent boundary layers Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 901 , 25 October 2020 , A28
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Balmforth, N., Del-Castillo-Negrete, D. & Young, W. R. 1997 Dynamics of vorticity defects in shear. J. Fluid Mech. 333, 197–230.CrossRefGoogle Scholar
Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1, 177–190.CrossRefGoogle Scholar
Bautista, J.-C. C., Ebadi, A., White, C. M., Chini, G. P. & Klewicki, J. C. 2019 A uniform momentum zone–vortical fissure model of the turbulent boundary layer. J. Fluid Mech. 858, 609–633.CrossRefGoogle Scholar
Beaume, C., Chini, G. P., Julien, K. & Knobloch, E. 2015 Reduced description of exact coherent states in parallel shear flows. Phys. Rev. E 91, 043010.CrossRefGoogle ScholarPubMed
Blackburn, H. M., Hall, P. & Sherwin, S. J. 2013 Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flows. J. Fluid Mech. 726, R2.CrossRefGoogle Scholar
Childress, S. 1979 Alph-effect in flux ropes and sheets. Phys. Earth Planet. Inter. 20, 172–180.CrossRefGoogle Scholar
Chini, G. P. 2008 Strongly nonlinear Langmuir circulation and Rayleigh–Bénard convection. J. Fluid Mech. 614, 39–65.CrossRefGoogle Scholar
Chini, G. P. 2016 Exact coherent structures at extreme Reynolds number. J. Fluid Mech. Focus on Fluids 794, 1–4.CrossRefGoogle Scholar
Chini, G. P. & Cox, S. M. 2009 Large Rayleigh number thermal convection: heat flux predictions and strongly nonlinear solutions. Phys. Fluids 21, 083603.CrossRefGoogle Scholar
Chini, G. P., Montemuro, B., White, C. M. & Klewicki, J. 2017 A self-sustaining process model of inertial layer dynamics in high Reynolds number turbulent wall flows. Phil. Trans. R. Soc. A 375, 20160090.CrossRefGoogle ScholarPubMed
Deguchi, K. 2015 Self-sustained states at Kolmogorov microscale. J. Fluid Mech. 781, R6.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014 a Free-stream coherent structures in parallel boundary-layer flows. J. Fluid Mech. 752, 602–625.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014 b The high-Reynolds-number asymptotic development of nonlinear equilibirum states in plane Couette flow. J. Fluid Mech. 750, 99–112.CrossRefGoogle Scholar
Dempsey, L. J., Deguchi, K., Hall, P. & Walton, A. G. 2016 Localised Tollmien–Schlichting wave interaction states in plane Poiseuille flow. J. Fluid Mech. 791, 97–121.CrossRefGoogle Scholar
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2008 Transition in pipe flow: the saddle structure on the boundary of turbulence. J. Fluid Mech. 613, 255–274.CrossRefGoogle Scholar
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2010 Slug genesis in cylindrical pipe flow. J. Fluid Mech. 663, 180–208.CrossRefGoogle Scholar
Eckhardt, B. & Zammert, S. 2018 Small scale exact coherent structures at large Reynolds numbers in plane Couette flow. Nonlinearity 31, R66–R77.CrossRefGoogle Scholar
Elsnab, J. R., Monty, J. P., White, C. M., Koochesfahani, M. M. & Klewicki, J. C. 2017 Efficacy of single-component MTV to measure turbulent wall-flow velocity derivative profiles at high resolution. Exp. Fluids 58, 128–139.CrossRefGoogle Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.CrossRefGoogle ScholarPubMed
Fan, D., Xu, J., Yao, M. X. & Hickey, J.-P. 2019 On the detection of internal interfacial layers in turbulent flows. J. Fluid Mech. 872, 198–217.CrossRefGoogle Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.CrossRefGoogle Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.CrossRefGoogle Scholar
Hall, P. 2018 Vortex–wave interaction arrays: a sustaining mechanism for the log layer? J. Fluid Mech. 850, 46–82.CrossRefGoogle Scholar
Hall, P. & Sherwin, S. J. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.CrossRefGoogle Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interaction in boundary layer transition. J. Fluid Mech. 227, 641–666.CrossRefGoogle Scholar
Harper, J. F. 1963 On boundary layers in two-dimensional flows with vorticity. J. Fluid Mech. 17 (1), 141–153.CrossRefGoogle Scholar
Hwang, Y. & Bengana, Y. 2016 Self-sustaining process of minimal attached eddies in turbulent channel flow. J. Fluid Mech. 795, 708–738.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105, 044505.CrossRefGoogle ScholarPubMed
Hwang, Y., Willis, A. P. & Cossu, C. 2016 Invariant solutions of minimal large-scale structures in turbulent channel flow for ${R}e_\tau$ up to 1000. J. Fluid Mech. 802, R1.CrossRefGoogle Scholar
Jiménez, J. & Zufiria, J. A. 1987 A boundary-layer analysis of Rayleigh–Bénard convection at large Rayleigh number. J. Fluid Mech. 178, 53–71.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.CrossRefGoogle Scholar
Klewicki, J. C. 2013 a A description of turbulent wall-flow vorticity consistent with mean dynamics. J. Fluid Mech. 737, 176–204.CrossRefGoogle Scholar
Klewicki, J. C. 2013 b On the singular nature of turbulent boundary layers. Procedia IUTAM 9, 69–78.CrossRefGoogle Scholar
Laskari, A., de Kat, R., Hearst, R. J. & Ganapathisubramani, B. 2018 Time evolution of uniform momentum zones in a turbulent boundary layer. J. Fluid Mech. 842, 554–590.CrossRefGoogle Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to $\mathit {Re}_\tau \approx 5200$. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lee, M. & Moser, R. D. 2018 Extreme-scale motions in turbulent plane Couette flows. J. Fluid Mech. 842, 128–145.CrossRefGoogle Scholar
Ludwig, D. 1966 Uniform asymptotic expansions at a caustic. Commun. Pure Appl. Maths 19, 215–250.CrossRefGoogle Scholar
McKee, W. 1973 Waves on a shearing current: a uniformly valid asymptotic solution. Proc. Camb. Phil. Soc. 75, 295–301.CrossRefGoogle Scholar
Meinhart, C. & Adrian, R. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694–696.CrossRefGoogle Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
Priyadarshana, P. J. A., Klewicki, J. C., Treat, S. & Foss, J. F. 2007 Statistical structure of turbulent boundary-layer velocity–vorticity products at high and low Reynolds numbers. J. Fluid Mech. 570, 307–346.CrossRefGoogle Scholar
Rawat, S., Coussu, C., Hwang, Y. & Rincon, F. 2015 On the self-sustained nature of large-scale motions in turbulent Couette flow. J. Fluid Mech. 782, 515–540.CrossRefGoogle Scholar
Rhines, P. B. & Young, W. R. 1983 How rapidly is a passive scalar mixed within closed streamlines? J. Fluid Mech. 133, 133–145.CrossRefGoogle Scholar
Saxton-Fox, T. & McKeon, B. J. 2017 Coherent structures, uniform momentum zones and the streamwise energy spectrum in wall-bounded turbulent flows. J. Fluid Mech. 826, R6.CrossRefGoogle Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.CrossRefGoogle Scholar
de Silva, C. M., Philip, J., Hutchins, N. & Marusic, I. 2017 Interfaces of uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 820, 451–478.CrossRefGoogle Scholar
Suri, B., Tithof, J., Grigoriev, R. O. & Schatz, M. F. 2017 Forecasting fluid flows using the geometry of turbulence. Phys. Rev. Lett. 118, 114501.CrossRefGoogle ScholarPubMed
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.CrossRefGoogle Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98, 204501.CrossRefGoogle ScholarPubMed
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.CrossRefGoogle Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar