Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-29T12:46:06.403Z Has data issue: false hasContentIssue false
  • English
  • Français

Separation scaling for viscous vortex reconnection

Published online by Cambridge University Press:  06 August 2020

Jie Yao Open the ORCID record for Jie Yao [Opens in a new window]  and
Fazle Hussain Open the ORCID record for Fazle Hussain [Opens in a new window]
Jie Yao
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX79409, USA
Fazle Hussain*
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX79409, USA
*
†Email address for correspondence: fazle.hussain@ttu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Reconnection plays a significant role in the dynamics of plasmas, polymers and macromolecules, as well as in numerous laminar and turbulent flow phenomena in both classical and quantum fluids. Extensive studies in quantum vortex reconnection show that the minimum separation distance $\delta$ between interacting vortices follows a $\delta(t) \sim t^{1/2}$ scaling. Due to the complex nature of the dynamics (e.g. the formation of bridges and threads as well as successive reconnections and avalanche), such scaling has never been reported for (classical) viscous vortex reconnection. Using direct numerical simulation of the Navier–Stokes equations, we study viscous reconnection of slender vortices, whose core size is much smaller than the radius of the vortex curvature. For separations that are large compared to the vortex core size, we discover that $\delta (t)$ between the two interacting viscous vortices surprisingly also follows the 1/2-power scaling for both pre- and post-reconnection events. The prefactors in this 1/2-power law are found to depend not only on the initial configuration but also on the vortex Reynolds number (or viscosity). Our finding in viscous reconnection, complementing numerous works on quantum vortex reconnection, suggests that there is indeed a universal route for reconnection – an essential result for understanding the various facets of the vortex reconnection phenomena and their potential modelling, as well as possibly explaining turbulence cascade physics.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex interactions
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 900 , 10 October 2020 , R4
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Allen, A. J., Zuccher, S., Caliari, M., Proukakis, N. P., Parker, N. G. & Barenghi, C. F. 2014 Vortex reconnections in atomic condensates at finite temperature. Phys. Rev. A 90 (1), 013601.CrossRefGoogle Scholar
Baggaley, A. W. 2012 The sensitivity of the vortex filament method to different reconnection models. J. Low Temp. Phys. 168 (1–2), 18–30.CrossRefGoogle Scholar
Baggaley, A. W. & Barenghi, C. F. 2011 Spectrum of turbulent Kelvin-waves cascade in superfluid helium. Phys. Rev. B 83 (13), 134509.CrossRefGoogle Scholar
Barenghi, C. F., Donnelly, R. J. & Vinen, W. F. 2001 Quantized Vortex Dynamics and Superfluid Turbulence. Springer Science & Business Media.CrossRefGoogle Scholar
Beardsell, G., Dufresne, L. & Dumas, G. 2016 Investigation of the viscous reconnection phenomenon of two vortex tubes through spectral simulations. Phys. Fluids 28 (9), 095103.CrossRefGoogle Scholar
Bewley, G. P., Paoletti, M. S., Sreenivasan, K. R. & Lathrop, D. P. 2008 Characterization of reconnecting vortices in superfluid helium. Proc. Natl Acad. Sci. 105 (37), 13707–13710.CrossRefGoogle ScholarPubMed
Boratav, O. N., Pelz, R. B. & Zabusky, N. J. 1992 Reconnection in orthogonally interacting vortex tubes: direct numerical simulations and quantifications. Phys. Fluids A 4 (3), 581–605.CrossRefGoogle Scholar
Boué, L., Khomenko, D., L'vov, V. S. & Procaccia, I. 2013 Analytic solution of the approach of quantum vortices towards reconnection. Phys. Rev. Lett. 111 (14), 145302.CrossRefGoogle ScholarPubMed
Chatelain, P., Kivotides, D. & Leonard, A. 2003 Reconnection of colliding vortex rings. Phys. Rev. Lett. 90 (5), 054501.CrossRefGoogle ScholarPubMed
Daryan, H., Hussain, F. & Hickey, J.-P. 2020 Aeroacoustic noise generation due to vortex reconnection. Phys. Rev. Fluids 5, 062702.CrossRefGoogle Scholar
Fonda, E., Meichle, D. P., Ouellette, N. T., Hormoz, S. & Lathrop, D. P. 2014 Direct observation of Kelvin waves excited by quantized vortex reconnection. Proc. Natl Acad. Sci. 111, 4707–4710.CrossRefGoogle ScholarPubMed
Fonda, E., Sreenivasan, K. R. & Lathrop, D. P. 2019 Reconnection scaling in quantum fluids. Proc. Natl Acad. Sci. 116 (6), 1924–1928.CrossRefGoogle ScholarPubMed
Galantucci, L., Baggaley, A. W., Parker, N. G. & Barenghi, C. F. 2019 Crossover from interaction to driven regimes in quantum vortex reconnections. Proc. Natl Acad. Sci. 116 (25), 12204–12211.CrossRefGoogle ScholarPubMed
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.CrossRefGoogle Scholar
Hussain, F. & Duraisamy, K. 2011 Mechanics of viscous vortex reconnection. Phys. Fluids 23 (2), 021701.CrossRefGoogle Scholar
Jaque, R. S. & Fuentes, O. V. 2017 Reconnection of orthogonal cylindrical vortices. Eur. J. Mech. B/Fluids 62, 51–56.CrossRefGoogle Scholar
Kida, S. & Takaoka, M. 1994 Vortex reconnection. Annu. Rev. Fluid Mech. 26 (1), 169–177.CrossRefGoogle Scholar
Kimura, Y. & Moffatt, H. K. 2017 Scaling properties towards vortex reconnection under Biot–Savart evolution. Fluid Dyn. Res. 50 (1), 011409.CrossRefGoogle Scholar
Kimura, Y. & Moffatt, H. K. 2018 A tent model of vortex reconnection under Biot–Savart evolution. J. Fluid Mech. 834, R1.CrossRefGoogle Scholar
Kivotides, D., Vassilicos, J. C., Samuels, D. C. & Barenghi, C. F. 2001 Kelvin waves cascade in superfluid turbulence. Phys. Rev. Lett. 86 (14), 3080–3083.CrossRefGoogle ScholarPubMed
Kleckner, D. & Irvine, W. T. M. 2013 Creation and dynamics of knotted vortices. Nat. Phys. 9 (4), 253–258.CrossRefGoogle Scholar
Koplik, J. & Levine, H. 1993 Vortex reconnection in superfluid helium. Phys. Rev. Lett. 71 (9), 1375–1378.CrossRefGoogle ScholarPubMed
Leadbeater, M., Winiecki, T., Samuels, D. C., Barenghi, C. F. & Adams, C. S. 2001 Sound emission due to superfluid vortex reconnections. Phys. Rev. Lett. 86 (8), 1410–1413.CrossRefGoogle ScholarPubMed
Melander, M. V. & Hussain, F. 1989 Cross-linking of two antiparallel vortex tubes. Phys. Fluids A 1 (4), 633–636.CrossRefGoogle Scholar
Moffatt, H. K. & Kimura, Y. 2019 a Towards a finite-time singularity of the Navier–Stokes equations. Part 1. Derivation and analysis of dynamical system. J. Fluid Mech. 861, 930–967.CrossRefGoogle Scholar
Moffatt, H. K. & Kimura, Y. 2019 b Towards a finite-time singularity of the Navier–Stokes equations. Part 2. Vortex reconnection and singularity evasion. J. Fluid Mech. 870, R1.CrossRefGoogle Scholar
Nazarenko, S. & West, R. 2003 Analytical solution for nonlinear Schrödinger vortex reconnection. J. Low Temp. Phys. 132 (1–2), 1–10.CrossRefGoogle Scholar
Paoletti, M. S., Fisher, M. E. & Lathrop, D. P. 2010 Reconnection dynamics for quantized vortices. Physica D 239 (14), 1367–1377.CrossRefGoogle Scholar
Priest, E. & Forbes, T. 2000 Magnetic Reconnection: MHD Theory and Applications. Cambridge University Press.CrossRefGoogle Scholar
Pumir, A. & Kerr, R. M. 1987 Numerical simulation of interacting vortex tubes. Phys. Rev. Lett. 58 (16), 1636–1639.CrossRefGoogle ScholarPubMed
Rorai, C., Skipper, J., Kerr, R. M. & Sreenivasan, K. R. 2016 Approach and separation of quantised vortices with balanced cores. J. Fluid Mech. 808, 641–667.CrossRefGoogle Scholar
Schwarz, K. W. 1985 Three-dimensional vortex dynamics in superfluid $^{4}\textrm {He}$: line–line and line–boundary interactions. Phys. Rev. B 31 (9), 5782–5804.CrossRefGoogle Scholar
Siggia, E. D. 1985 Collapse and amplification of a vortex filament. Phys. Fluids 28 (3), 794–805.CrossRefGoogle Scholar
Siggia, E. D. & Pumir, A. 1985 Incipient singularities in the Navier–Stokes equations. Phys. Rev. Lett. 55 (17), 1749–1752.CrossRefGoogle ScholarPubMed
Vazquez, M. & De Witt, S. 2004 Tangle analysis of gin site-specific recombination. Math. Proc. Camb. Phil. Soc. 136, 565–582.CrossRefGoogle Scholar
Villois, A., Krstulovic, G., Proment, D. & Salman, H. 2016 A vortex filament tracking method for the Gross–Pitaevskii model of a superfluid. J. Phys. A 49 (41), 415502.CrossRefGoogle Scholar
Villois, A., Proment, D. & Krstulovic, G. 2017 Universal and nonuniversal aspects of vortex reconnections in superfluids. Phys. Rev. Fluids 2 (4), 044701.CrossRefGoogle Scholar
Vinen, W. F., Tsubota, M. & Mitani, A. 2003 Kelvin-wave cascade on a vortex in superfluid $^{4}\textrm {He}$ at a very low temperature. Phys. Rev. Lett. 91 (13), 135301–135304.CrossRefGoogle Scholar
de Waele, A. T. A. M. & Aarts, R. G. K. M. 1994 Route to vortex reconnection. Phys. Rev. Lett. 72, 482–485.CrossRefGoogle ScholarPubMed
Yao, J. & Hussain, F. 2020 a On singularity formation via viscous vortex reconnection. J. Fluid Mech. 888, R2.CrossRefGoogle Scholar
Yao, J. & Hussain, F. 2020 b A physical model of turbulence cascade via vortex reconnection sequence and avalanche. J. Fluid Mech. 883, A51.CrossRefGoogle Scholar
Zuccher, S., Caliari, M., Baggaley, A. W. & Barenghi, C. F. 2012 Quantum vortex reconnections. Phys. Fluids 24 (12), 125108.CrossRefGoogle Scholar

Yao and Hussainy supplementary movie 1

Evolution of flow structures for reconnection of colliding vortex rings at Re Γ = 2000 using direct numerical simulation of Naiver-Stokes equation. The radius of the vortex ring is R=1 and the initial minimum distance between two rings is δ0 = 0.2. The flow structures are represented by vorticity isosurface at 5% of maximum initial vorticity |ω| = 0.05ω0.

Download Yao and Hussainy supplementary movie 1(Video)
Video 7.1 MB

Yao and Hussainy supplementary movie 2

Evolution of vortex axis for reconnection of colliding vortex rings at ReΓ = 2000

Download Yao and Hussainy supplementary movie 2(Video)
Video 1.4 MB

Yao and Hussainy supplementary movie 3

Evolution of vortex axis for reconnection of colliding vortex rings at ReΓ = 2000

Download Yao and Hussainy supplementary movie 3(Video)
Video 3.1 MB

Yao and Hussainy supplementary movie 4

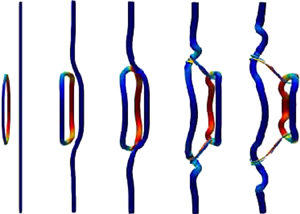
Evolution of vortex axis for reconnection of orthogonal straight vortex tubes at ReΓ= 2000.

Download Yao and Hussainy supplementary movie 4(Video)
Video 1.4 MB

Yao and Hussainy supplementary movie 5

Evolution of flow structures for reconnection of vortex ring with a straight tube at ReΓ= 2000 using direct numerical simulation of Naiver-Stokes equation. The radius of the vortex ring is R = 1 and the initial minimum distance is δ0 = 0.4. The flow structures are represented by vorticity isosurface at 5% of maximum initial vorticity |ω| = 0.05ω0 .

Download Yao and Hussainy supplementary movie 5(Video)
Video 7.4 MB

Yao and Hussainy supplementary movie 6

Evolution of vortex axis for reconnection of vortex ring with a straight tube at ReΓ= 2000

Download Yao and Hussainy supplementary movie 6(Video)
Video 2.6 MB
Supplementary material: PDF

Yao and Hussainy supplementary material

Supplementary data

Download Yao and Hussainy supplementary material(PDF)
PDF 879.3 KB