Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T07:42:00.810Z Has data issue: false hasContentIssue false
  • English
  • Français

Separations and secondary structures due to unsteady flow in a curved pipe

Published online by Cambridge University Press:  14 February 2017

C. Vamsi Krishna Open the ORCID record for C. Vamsi Krishna [Opens in a new window] ,
Namrata Gundiah  and
Jaywant H. Arakeri
C. Vamsi Krishna
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560012, Karnataka, India
Namrata Gundiah
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560012, Karnataka, India
Jaywant H. Arakeri*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560012, Karnataka, India
*
†Email address for correspondence: jaywant@mecheng.iisc.ernet.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Unsteady flows in highly curved geometries are of interest in many engineering applications and also in physiological flows. In this study, we use flow visualization and computational fluid dynamics to study unsteady flows in a highly curved tube (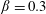$\unicode[STIX]{x1D6FD}=0.3$) with square cross-section; here, 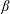$\unicode[STIX]{x1D6FD}$ is the ratio of the half edge length to the radius of curvature of the tube. To explore the combined effects of curvature and pulsatility, we use a single flow pulse of duration 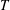$T$ and peak area averaged axial velocity $U_{p(max)}$, which are independently varied to investigate a range of Dean and Womersley numbers. This range includes cases corresponding to flows in the ascending aorta. We observe radially inward moving secondary flows which have the structure of wall jets on the straight walls; their subsequent collision on the inner wall leads to a re-entrant radially outward moving jet. The wall jet arises due to an imbalance between the centrifugal force and the radial pressure gradient. During the deceleration phase, the low-axial-momentum fluid accumulated in the jet reverses direction and leads to flow separation near the inner wall. We use boundary layer equations to derive scales, which have not been reported earlier, for the secondary flow velocities, the wall shear stress components and the distance (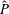$\hat{P}$) traversed by the secondary flow structures in the transverse plane. We show that 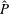$\hat{P}$ predicts the movement of vortical structures until collision. In the limit 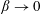$\unicode[STIX]{x1D6FD}\rightarrow 0$, the Reynolds number based on this secondary flow velocity scale asymptotes to the secondary streaming Reynolds number proposed by Lyne (J. Fluid Mech., vol. 45 (01), 1971, pp. 13–31) in loosely curved pipes. The magnitude of the secondary flow velocity is high and 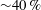${\sim}40\,\%$ of 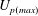$U_{p(max)}$ for physiological flow conditions. We show that the flow separation on the inner wall has origins in the secondary flow, which was reported in a few earlier studies, and is not due to the axial pressure gradient in the tube as proposed earlier. The wall shear stress components, hypothesized to be important in arterial mechanobiology, may be estimated using our scaling relations for geometries with different curvatures and varying pulsatilities.

JFM classification

Boundary Layers: Boundary layer separation Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 26 - 59
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agrawal, Y., Talbot, L. & Gong, K. 1978 Laser anemometer study of flow development in curved circular pipes. J. Fluid Mech. 85 (03), 497–518.Google Scholar
Babu, A. R., Byju, A. G. & Gundiah, N. 2015 Biomechanical properties of human ascending thoracic aortic dissections. Trans. ASME J. Biomech. Engng 137 (8), 081013.Google Scholar
Bara, B., Nandakumar, K. & Masliyah, J. H. 1992 An experimental and numerical study of the Dean problem: flow development towards two-dimensional multiple solutions. J. Fluid Mech. 244, 339–376.Google Scholar
Barua, S. N. 1963 On secondary flow in stationary curved pipes. Q. J. Mech. Appl. Maths 16 (1), 61–77.Google Scholar
Berger, S. A., Talbot, L. & Yao, L. S. 1983 Flow in curved pipes. Annu. Rev. Fluid Mech. 15 (1), 461–512.CrossRefGoogle Scholar
Berk, B. C. 2008 Atheroprotective signaling mechanisms activated by steady laminar flow in endothelial cells. Circulation 117 (8), 1082–1089.Google Scholar
Bertelsen, A. F. 1975 An experimental investigation of low Reynolds number secondary streaming effects associated with an oscillating viscous flow in a curved pipe. J. Fluid Mech. 70 (3), 519–527.Google Scholar
Boiron, O., Deplano, V. & Pelissier, R. 2007 Experimental and numerical studies on the starting effect on the secondary flow in a bend. J. Fluid Mech. 574, 109–129.Google Scholar
Bulusu, K. V. & Plesniak, M. W. 2013 Secondary flow morphologies due to model stent-induced perturbations in a 180° curved tube during systolic deceleration. Exp. Fluids 54 (3), 1–13.CrossRefGoogle Scholar
Chandran, K. B. 1993 Flow dynamics in the human aorta. Trans. ASME J. Biomech. Engng 115 (4B), 611–616.Google Scholar
Chandran, K. B. & Yearwood, T. L. 1981 Experimental study of physiological pulsatile flow in a curved tube. J. Fluid Mech. 111, 59–85.Google Scholar
Chang, L. J. & Tarbell, J. M. 1985 Numerical simulation of fully developed sinusoidal and pulsatile (physiological) flow in curved tubes. J. Fluid Mech. 161, 175–198.CrossRefGoogle Scholar
Chien, S. 2007 Mechanotransduction and endothelial cell homeostasis: the wisdom of the cell. American J. Physiol.-Heart Circulat. Physiol. 292 (3), H1209–H1224.Google Scholar
Chien, S. 2008 Effects of disturbed flow on endothelial cells. Ann. Biomed. Engng 36 (4), 554–562.CrossRefGoogle ScholarPubMed
Chiu, J.-J. & Chien, S. 2011 Effects of disturbed flow on vascular endothelium: pathophysiological basis and clinical perspectives. Physiol. Rev. 91 (1), 327–387.Google Scholar
Choi, U. S., Talbot, L. & Cornet, I. 1979 Experimental study of wall shear rates in the entry region of a curved tube. J. Fluid Mech. 93 (03), 465–489.Google Scholar
Clarke, R. & Denier, J. P. 2009 The decay of suddenly-blocked flow in a curved pipe. J. Engng Maths 63, 241–257.Google Scholar
Collins, W. M. & Dennis, S. C. R. 1975 The steady motion of a viscous fluid in a curved tube. Q. J. Mech. Appl. Maths 28 (2), 133–156.Google Scholar
Cowley, S. J., Van Dommelen, L. L. & Lam, S. T. 1990 On the use of Lagrangian variables in descriptions of unsteady boundary-layer separation. Phil. Trans. R. Soc. Lond. A 333 (1631), 343–378.Google Scholar
Currier, J. M. & Fung, K.-Y. 1992 Analysis of the onset of dynamic stall. AIAA J. 30 (10), 2469–2477.Google Scholar
Das, D.1998 Evolution and instability of unsteady boundary layers with reverse flow. PhD thesis, Indian Institute of Science, Bangalore.Google Scholar
Das, D. & Arakeri, J. H. 1998 Transition of unsteady velocity profiles with reverse flow. J. Fluid Mech. 374, 251–283.Google Scholar
Das, P., Govardhan, R. N. & Arakeri, J. H. 2013a Effect of hinged leaflets on vortex pair generation. J. Fluid Mech. 730, 626–658.Google Scholar
Das, S. P., Srinivasan, U. & Arakeri, J. H. 2013b Unsteady separation and vortex shedding from a laminar separation bubble over a bluff body. J. Fluids Struct. 40, 233–245.Google Scholar
Das, S. P., Srinivasan, U. & Arakeri, J. H. 2016 Instabilities in unsteady boundary layers with reverse flow. Eur. J. Mech. (B/Fluids) 55, 49–62.CrossRefGoogle Scholar
Davies, P. F. 1995 Flow-mediated endothelial mechanotransduction. Physiol. Rev. 75 (3), 519–560.Google Scholar
Davies, P. F. 2009 Hemodynamic shear stress and the endothelium in cardiovascular pathophysiology. Nature Clin. Practice Cardiovasc. Med. 6 (1), 16–26.CrossRefGoogle ScholarPubMed
Dean, W. R. 1927 XVI. Note on the motion of fluid in a curved pipe. Lond. Edin. Dublin Phil. Mag. J. Sci. 4 (20), 208–223.Google Scholar
Dean, W. R. 1928 LXXII. The stream-line motion of fluid in a curved pipe (second paper). Lond. Edin. Dublin Phil. Mag. J. Sci. 5 (30), 673–695.CrossRefGoogle Scholar
Del Pino, C., Hewitt, R. E., Clarke, R. J., Mullin, T. & Denier, J. P. 2008 Unsteady fronts in the spin-down of a fluid-filled torus. Phys. Fluids 20 (12), 124104.Google Scholar
Dennis, S. C. R. & Ng, M. 1982 Dual solutions for steady laminar flow through a curved tube. Q. J. Mech. Appl. Maths 35 (3), 305–324.CrossRefGoogle Scholar
Dennis, S. C. R. & Riley, N. 1991 On the fully developed flow in a curved pipe at large Dean number. Proc. R. Soc. Lond. A 434, 473–478.Google Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Glenn, A. L., Bulusu, K. V., Shu, F. & Plesniak, M. W. 2012 Secondary flow structures under stent-induced perturbations for cardiovascular flow in a curved artery model. Intl J. Heat Fluid Flow 35, 76–83.Google Scholar
Hamakiotes, C. C. & Berger, S. A. 1988 Fully developed pulsatile flow in a curved pipe. J. Fluid Mech. 195, 23–55.Google Scholar
Hewitt, R. E., Hazel, A. L., Clarke, R. J. & Denier, J. P. 2011 Unsteady flow in a rotating torus after a sudden change in rotation rate. J. Fluid Mech. 688, 88–119.Google Scholar
Humphery, J. D. 2002 Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer.CrossRefGoogle Scholar
Itō, H. 1969 Laminar flow in curved pipes. Z. Angew. Math. Mech. 49 (11), 653–663.CrossRefGoogle Scholar
Jarrahi, M., Castelain, C. & Peerhossaini, H. 2011 Laminar sinusoidal and pulsatile flows in a curved pipe. J. Appl. Fluid Mech. 4 (2‐s1), 21–26.Google Scholar
Kalpakli, A., Örlü, R., Tillmark, N. & Alfredsson, P. H. 2011 Pulsatile turbulent flow through pipe bends at high Dean and Womersley numbers. J. Phys.: Conf. Ser. 318, 092023.Google Scholar
Komai, Y. & Tanishita, K. 1997 Fully developed intermittent flow in a curved tube. J. Fluid Mech. 347, 263–287.Google Scholar
Konno, T., Satoh, Y. & Tanishita, K. 1994 Secondary flow augmentation in the diastolic phase of physiologically intermittent flow in a curved tube. Biofluid Mech. 17 (107), 205–215.Google Scholar
Koumoutsakos, P. & Leonard, A. 1995 High-resolution simulations of the flow around an impulsively started cylinder using vortex methods. J. Fluid Mech. 296, 1–38.Google Scholar
Krueger, P. S. & Gharib, M. 2003 The significance of vortex ring formation to the impulse and thrust of a starting jet. Phys. Fluids 15 (5), 1271–1281.Google Scholar
Ku, D. N. 1997 Blood flow in arteries. Annu. Rev. Fluid Mech. 29 (1), 399–434.Google Scholar
Ku, D. N., Giddens, D. P., Zarins, C. K. & Glagov, S. 1985 Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress. Arterioscler. Thromb. Vasc. Biol. 5 (3), 293–302.Google Scholar
Lantz, J., Renner, J., Länne, T. & Karlsson, M. 2015 Is aortic wall shear stress affected by aging? An image-based numerical study with two age groups. Med. Engng Phys. 37 (3), 265–271.Google Scholar
Lyne, W. H. 1971 Unsteady viscous flow in a curved pipe. J. Fluid Mech. 45 (01), 13–31.Google Scholar
Machane, W. 2010 Bifurcation and stability analysis of laminar flow in curved ducts. Intl J. Numer. Meth. Fluids 64 (4), 355–375.Google Scholar
McConalogue, D. J. & Srivastava, R. S. 1968 Motion of a fluid in a curved tube. Proc. R. Soc. Lond. A 307, 37–53.Google Scholar
Mees, P. A. J., Nandakumar, K. & Masliyah, J. H. 1996 Instability and transitions of flow in a curved square duct: the development of two pairs of Dean vortices. J. Fluid Mech. 314, 227–246.Google Scholar
Mondal, R. N., Kaga, Y., Hyakutake, T. & Yanase, S. 2007 Bifurcation diagram for two-dimensional steady flow and unsteady solutions in a curved square duct. Fluid Dyn. Res. 39 (5), 413–446.Google Scholar
Mori, Y. & Nakayama, W. 1965 Study on forced convective heat transfer in curved pipes. I – Laminar region (laminar forced convective heat transfer in curved pipe, noting Dean, Prandtl and Nusselt number ratios). Intl J. Heat Mass Transfer 8, 67–82.Google Scholar
Morris, L., Delassus, P., Callanan, A., Walsh, M., Wallis, F., Grace, P. & McGloughlin, T. 2005 3-D numerical simulation of blood flow through models of the human aorta. Trans. ASME J. Biomech. Engng 127 (5), 767–775.Google Scholar
Mullin, T. & Greated, C. A. 1980a Oscillatory flow in curved pipes. Part 1. The developing-flow case. J. Fluid Mech. 98 (02), 383–395.CrossRefGoogle Scholar
Mullin, T. & Greated, C. A. 1980b Oscillatory flow in curved pipes. Part 2. The fully developed case. J. Fluid Mech. 98 (02), 397–416.Google Scholar
Munson, B. R. 1975 Experimental results for oscillating flow in a curved pipe. Phys. Fluids 18 (12), 1607–1609.Google Scholar
Passerini, A. G., Milsted, A. & Rittgers, S. E. 2003 Shear stress magnitude and directionality modulate growth factor gene expression in preconditioned vascular endothelial cells. J. Vascu. Surg. 37 (1), 182–190.Google Scholar
Riley, N. 1998 Unsteady fully-developed flow in a curved pipe. J. Engng Maths 34 (1–2), 131–141.CrossRefGoogle Scholar
Rindt, C. C. M., Van Steenhoven, A. A., Janssen, J. D. & Vossers, G. 1991 Unsteady entrance flow in a 90 curved tube. J. Fluid Mech. 226, 445–474.Google Scholar
Shih, C., Lourenco, L., Van Dommelen, L. & Krothapalli, A. 1992 Unsteady flow past an airfoil pitching at a constant rate. AIAA J. 30 (5), 1153–1161.CrossRefGoogle Scholar
Siggers, J. H. & Waters, S. L. 2005 Steady flows in pipes with finite curvature. Phys. Fluids 17 (7), 077102.CrossRefGoogle Scholar
Siggers, J. H. & Waters, S. L. 2008 Unsteady flows in pipes with finite curvature. J. Fluid Mech. 600, 133–165.Google Scholar
Singh, M. P. 1974 Entry flow in a curved pipe. J. Fluid Mech. 65 (03), 517–539.Google Scholar
Singh, M. P., Sinha, P. C. & Aggarwal, M. 1978 Flow in the entrance of the aorta. J. Fluid Mech. 87 (01), 97–120.CrossRefGoogle Scholar
Smith, F. T. 1975 Pulsatile flow in curved pipes. J. Fluid Mech. 71 (01), 15–42.Google Scholar
Stewartson, K., Cebeci, T. & Chang, K. C. 1980 A boundary-layer collision in a curved duct. Q. J. Mech. Appl. Maths 33 (1), 59–75.Google Scholar
Sudo, K., Sumida, M. & Yamane, R. 1992 Secondary motion of fully developed oscillatory flow in a curved pipe. J. Fluid Mech. 237, 189–208.Google Scholar
Talbot, L. & Gong, K. O. 1983 Pulsatile entrance flow in a curved pipe. J. Fluid Mech. 127, 1–25.CrossRefGoogle Scholar
Timité, B., Castelain, C. & Peerhossaini, H. 2010 Pulsatile viscous flow in a curved pipe: effects of pulsation on the development of secondary flow. Intl J. Heat Fluid Flow 31 (5), 879–896.Google Scholar
Topper, J. N. & Gimbrone, M. A. Jr 1999 Blood flow and vascular gene expression: fluid shear stress as a modulator of endothelial phenotype. Mol. Med. Today 5 (1), 40–46.Google Scholar
Van Dommelen, L. L. & Cowley, S. J. 1990 On the Lagrangian description of unsteady boundary-layer separation. Part 1. General theory. J. Fluid Mech. 210, 593–626.Google Scholar
Van Dommelen, L. L. & Shen, S. F. 1980 The spontaneous generation of the singularity in a separating laminar boundary layer. J. Comput. Phys. 38 (2), 125–140.Google Scholar
Wang, C., Baker, B. M., Chen, C. S. & Schwartz, M. A. 2013 Endothelial cell sensing of flow direction. Arterioscler. Thromb. Vasc. Biol. 33 (9), 2130–2136.Google Scholar
Waters, S. L. & Pedley, T. J. 1999 Oscillatory flow in a tube of time-dependent curvature. Part 1. Perturbation to flow in a stationary curved tube. J. Fluid Mech. 383, 327–352.CrossRefGoogle Scholar
Winters, K. H. 1987 A bifurcation study of laminar flow in a curved tube of rectangular cross-section. J. Fluid Mech. 180, 343–369.Google Scholar
Yearwood, T. L. & Chandran, K. B. 1982 Physiological pulsatile flow experiments in a model of the human aortic arch. J. Biomech. 15 (9), 683–704.Google Scholar
Zalosh, R. G. & Nelson, W. G. 1973 Pulsating flow in a curved tube. J. Fluid Mech. 59, 693–705.CrossRefGoogle Scholar

Krishna et al. supplementary movie

Experimental PLIF flow visualizations and numerical simulations for case 2: Re ~ 3842, De ~ 2104, d/a ~ 0.29, and a ~ 32. We see evolution of the flow structures in the medial and transverse planes for the temporal variation of piston velocity shown in the left panel. The secondary structures impinge on the inner wall where they collide; subsequently the flow separates in the medial plane. Numerical simulations show axial velocity contours and velocity vectors. The colour bar shows the axial velocity normalized by Up(max). This video is slowed by 2x for ease of viewing.

Download Krishna et al. supplementary movie(Video)
Video 6.3 MB

Krishna et al. supplementary movie

Experimental flow visualizations and numerical simulations for case 3: Re ~ 3622, De ~ 1983, d/a ~ 0.20, and a ~ 45. In contrast to Movie 1, the input velocity pulse is shorter, and we see that the secondary structures do not reach the medial plane; hence no separation is observed. However, we see instability on the inner wall at the end of time pulse. This video is slowed by 3.5x for ease of viewing.

Download Krishna et al. supplementary movie(Video)
Video 5.1 MB

Krishna et al. supplementary movie

This case (Re ~ 3622, De ~ 1984, d/a ~ 0.41, and a ~ 23) corresponds to the longest time pulse. In contrast to Movies 1 and 2, the secondary structures impinge on the inner wall prior to stop of the piston; separation is observed at the beginning of the deceleration phase itself. This video is slowed by 1.5x for ease of viewing.

Download Krishna et al. supplementary movie(Video)
Video 10.2 MB