Article contents
Shear reversal in dense suspensions: the challenge to fabric evolution models from simulation data
Published online by Cambridge University Press: 29 May 2018
Abstract
Dense suspensions of hard particles are important as industrial or environmental materials (e.g. fresh concrete, food, paint or mud). To date, most constitutive models developed to describe them are, explicitly or effectively, ‘fabric evolution models’ based on: (i) a stress rule connecting the macroscopic stress to a second-rank microstructural fabric tensor 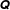 $\unicode[STIX]{x1D64C}$ ; and (ii) a closed time-evolution equation for
$\unicode[STIX]{x1D64C}$ ; and (ii) a closed time-evolution equation for 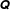 $\unicode[STIX]{x1D64C}$ . In dense suspensions, most of the stress comes from short-ranged pairwise steric or lubrication interactions at near-contacts (suitably defined), so a natural choice for
$\unicode[STIX]{x1D64C}$ . In dense suspensions, most of the stress comes from short-ranged pairwise steric or lubrication interactions at near-contacts (suitably defined), so a natural choice for  $\unicode[STIX]{x1D64C}$ is the deviatoric second moment of the distribution
$\unicode[STIX]{x1D64C}$ is the deviatoric second moment of the distribution 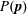 $P(\boldsymbol{p})$ of the near-contact orientations
$P(\boldsymbol{p})$ of the near-contact orientations 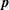 $\boldsymbol{p}$ . Here we test directly whether a closed time-evolution equation for such a
$\boldsymbol{p}$ . Here we test directly whether a closed time-evolution equation for such a 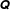 $\unicode[STIX]{x1D64C}$ can exist, for the case of inertialess non-Brownian hard spheres in a Newtonian solvent. We perform extensive numerical simulations accessing high levels of detail for the evolution of
$\unicode[STIX]{x1D64C}$ can exist, for the case of inertialess non-Brownian hard spheres in a Newtonian solvent. We perform extensive numerical simulations accessing high levels of detail for the evolution of 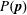 $P(\boldsymbol{p})$ under shear reversal, providing a stringent test for fabric evolution models. We consider a generic class of these models as defined by Hand (J. Fluid Mech., vol. 13, 1962, pp. 33–46) that assumes little as to the micromechanical behaviour of the suspension and is only constrained by frame indifference. Motivated by the smallness of microstructural anisotropies in the dense regime, we start with linear models in this class and successively consider those increasingly nonlinear in
$P(\boldsymbol{p})$ under shear reversal, providing a stringent test for fabric evolution models. We consider a generic class of these models as defined by Hand (J. Fluid Mech., vol. 13, 1962, pp. 33–46) that assumes little as to the micromechanical behaviour of the suspension and is only constrained by frame indifference. Motivated by the smallness of microstructural anisotropies in the dense regime, we start with linear models in this class and successively consider those increasingly nonlinear in 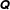 $\unicode[STIX]{x1D64C}$ . Based on these results, we suggest that no closed fabric evolution model properly describes the dynamics of the fabric tensor under reversal. We attribute this to the fact that, while a second-rank tensor captures reasonably well the microstructure in steady flows, it gives a poor description during significant parts of the microstructural evolution following shear reversal. Specifically, the truncation of
$\unicode[STIX]{x1D64C}$ . Based on these results, we suggest that no closed fabric evolution model properly describes the dynamics of the fabric tensor under reversal. We attribute this to the fact that, while a second-rank tensor captures reasonably well the microstructure in steady flows, it gives a poor description during significant parts of the microstructural evolution following shear reversal. Specifically, the truncation of 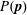 $P(\boldsymbol{p})$ at second spherical harmonic (or second-rank tensor) level describes ellipsoidal distributions of near-contact orientations, whereas on reversal we observe distributions that are markedly four-lobed; moreover,
$P(\boldsymbol{p})$ at second spherical harmonic (or second-rank tensor) level describes ellipsoidal distributions of near-contact orientations, whereas on reversal we observe distributions that are markedly four-lobed; moreover,  ${\dot{P}}(\boldsymbol{p})$ has oblique axes, not collinear with those of
${\dot{P}}(\boldsymbol{p})$ has oblique axes, not collinear with those of 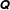 $\unicode[STIX]{x1D64C}$ in the shear plane. This structure probably precludes any adequate closure at second-rank level. Instead, our numerical data suggest that closures involving the coupled evolution of both a fabric tensor and a fourth-rank tensor might be reasonably accurate.
$\unicode[STIX]{x1D64C}$ in the shear plane. This structure probably precludes any adequate closure at second-rank level. Instead, our numerical data suggest that closures involving the coupled evolution of both a fabric tensor and a fourth-rank tensor might be reasonably accurate.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 34
- Cited by


