Published online by Cambridge University Press: 12 April 2018
Naturally developing and acoustically excited shear layers at the Reynolds numbers 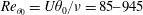 $Re_{\unicode[STIX]{x1D703}_{0}}=U\unicode[STIX]{x1D703}_{0}/\unicode[STIX]{x1D708}=85{-}945$ are studied using the hot-wire (HW) anemometry and particle image velocimetry (PIV), with a focus on the shear/rotation competition during the initial Kelvin–Helmholtz (KH) roll-up. Velocity spectra and the spatial linear stability (LST) analysis characterize the fundamental (
$Re_{\unicode[STIX]{x1D703}_{0}}=U\unicode[STIX]{x1D703}_{0}/\unicode[STIX]{x1D708}=85{-}945$ are studied using the hot-wire (HW) anemometry and particle image velocimetry (PIV), with a focus on the shear/rotation competition during the initial Kelvin–Helmholtz (KH) roll-up. Velocity spectra and the spatial linear stability (LST) analysis characterize the fundamental (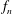 $f_{n}$) and its subharmonic (
$f_{n}$) and its subharmonic (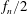 $f_{n}/2$) mode interacting due to the vortex pairing. For
$f_{n}/2$) mode interacting due to the vortex pairing. For 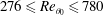 $276\leqslant Re_{\unicode[STIX]{x1D703}_{0}}\leqslant 780$, the root-mean-square (r.m.s.) of the streamwise turbulence intensity shows a double-peaking phenomenon, i.e. major and minor peaks of the
$276\leqslant Re_{\unicode[STIX]{x1D703}_{0}}\leqslant 780$, the root-mean-square (r.m.s.) of the streamwise turbulence intensity shows a double-peaking phenomenon, i.e. major and minor peaks of the 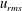 $u_{rms}$ coexist towards the high-speed (HS) and the low-speed (LS) sides, respectively. The single/double-peaked
$u_{rms}$ coexist towards the high-speed (HS) and the low-speed (LS) sides, respectively. The single/double-peaked 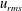 $u_{rms}$ profiles are found to be correlated with the scattered/organized distribution of the shear/rotation, demonstrating a transitioning character with the downstream distance,
$u_{rms}$ profiles are found to be correlated with the scattered/organized distribution of the shear/rotation, demonstrating a transitioning character with the downstream distance, 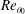 $Re_{\unicode[STIX]{x1D703}_{0}}$ and the upstream turbulence levels. The rotating vortex cores and the corresponding peripheral shear regions, demonstrate the phase reversal of the velocity fluctuations with respect to the HS and the LS sides. Excitation at
$Re_{\unicode[STIX]{x1D703}_{0}}$ and the upstream turbulence levels. The rotating vortex cores and the corresponding peripheral shear regions, demonstrate the phase reversal of the velocity fluctuations with respect to the HS and the LS sides. Excitation at 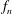 $f_{n}$ increases the vortex count by 21 %, advances the location of the first KH roll-up and hence also the minor peak formation location. Due to the enhanced pairing at the
$f_{n}$ increases the vortex count by 21 %, advances the location of the first KH roll-up and hence also the minor peak formation location. Due to the enhanced pairing at the 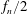 $f_{n}/2$ forcing, the vortex count reduces by 23 %. Before merging into the downstream rotation core, the upstream vortex is shifted towards the HS side and the major peak is accordingly augmented. Actuation advances the transition to the nonlinear state, as well as the saturation of the amplification factor. The volumetric topologies of the shear/rotation loops tracked in consecutive phases during the period of the acoustic excitation, separate from the edge and grow in time–space due to the viscous diffusion. The shearing and rotating loops are found to be associated with the thinning (elongation) and expansion (accumulation) of the vorticity, respectively.
$f_{n}/2$ forcing, the vortex count reduces by 23 %. Before merging into the downstream rotation core, the upstream vortex is shifted towards the HS side and the major peak is accordingly augmented. Actuation advances the transition to the nonlinear state, as well as the saturation of the amplification factor. The volumetric topologies of the shear/rotation loops tracked in consecutive phases during the period of the acoustic excitation, separate from the edge and grow in time–space due to the viscous diffusion. The shearing and rotating loops are found to be associated with the thinning (elongation) and expansion (accumulation) of the vorticity, respectively.
Movie 1. Shear/rotation loops obtained from the planar phase-locked PIV measurements interpolated into volumetric topologies. The phases ϕ=00, 600, 1200, 1800, 2400, 3000 during the acoustic actuation of the fundamental mode animate the shear (blue) and rotation (red) loops of the <Q>p-criterion passed through the vorticity cut-planes (green). The shear loops are found correlated with the thinning in the stretched vorticity zones while the rotating loops intersect with the expansion/accumulation of the vorticity.