Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-14T17:34:34.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Ship waves on uniform shear current at finite depth: wave resistance and critical velocity

Published online by Cambridge University Press:  24 February 2016

Yan Li  and
Simen Å Ellingsen Open the ORCID record for Simen Å Ellingsen [Opens in a new window]
Yan Li
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
Simen Å Ellingsen*
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
*
†Email address for correspondence: simen.a.ellingsen@ntnu.no
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a comprehensive theory for linear gravity-driven ship waves in the presence of a shear current with uniform vorticity, including the effects of finite water depth. The wave resistance in the presence of shear current is calculated for the first time, containing in general a non-zero lateral component. While formally apparently a straightforward extension of existing deep water theory, the introduction of finite water depth is physically non-trivial, since the surface waves are now affected by a subtle interplay of the effects of the current and the sea bed. This becomes particularly pronounced when considering the phenomenon of critical velocity, the velocity at which transversely propagating waves become unable to keep up with the moving source. The phenomenon is well known for shallow water, and was recently shown to exist also in deep water in the presence of a shear current (Ellingsen, J. Fluid Mech., vol. 742, 2014, R2). We derive the exact criterion for criticality as a function of an intrinsic shear Froude number 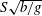$S\sqrt{b/g}$ (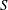$S$ is uniform vorticity, 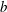$b$ size of source), the water depth and the angle between the shear current and the ship’s motion. Formulae for both the normal and lateral wave resistance forces are derived, and we analyse their dependence on the source velocity (or Froude number 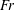$Fr$) for different amounts of shear and different directions of motion. The effect of the shear current is to increase wave resistance for upstream ship motion and decrease it for downstream motion. Also the value of 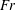$Fr$ at which 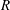$R$ is maximal is lowered for upstream and increased for downstream directions of ship motion. For oblique angles between ship motion and current there is a lateral wave resistance component which can amount to 10–20 % of the normal wave resistance for side-on shear and 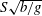$S\sqrt{b/g}$ of order unity. The theory is fully laid out and far-field contributions are carefully separated off by means of Cauchy’s integral theorem, exposing potential pitfalls associated with a slightly different method (Sokhotsky–Plemelj) used in several previous works.

JFM classification

Waves/Free-surface Flows: Shear waves Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 539 - 567
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bender, C. M. & Orszag, S. A. 1991 Advanced Mathematical Methods for Scientists and Engineers. Springer.Google Scholar
Benzaquen, M., Darmon, A. & Raphaël, E. 2014 Wake pattern and wave resistance for anisotropic moving disturbances. Phys. Fluids 26, 092106.CrossRefGoogle Scholar
Brown, E. D., Buchsbaum, S. B., Hall, R. E., Penhune, J. P., Schmitt, K. F., Watson, K. M. & Wyatt, D. C. 1989 Observations of a nonlinear solitary wave packet in the Kelvin wake of a ship. J. Fluid Mech. 204, 263–293.CrossRefGoogle Scholar
Bühler, O. 2009 Waves and Mean Flow. Cambridge University Press.CrossRefGoogle Scholar
Craik, A. D. D. 1968 Resonant gravity–wave interactions in a shear flow. J. Fluid Mech. 34, 531–549.CrossRefGoogle Scholar
Darmon, A., Benzaquen, M. & Raphaël, E. 2014 Kelvin wake pattern at large Froude numbers. J. Fluid Mech. 738, R3.CrossRefGoogle Scholar
Ellingsen, S. Å 2014a Initial surface disturbance on a shear current: The Cauchy–Poisson problem with a twist. Phys. Fluids 26, 082104.CrossRefGoogle Scholar
Ellingsen, S. Å. 2014b Ship waves in the presence of uniform vorticity. J. Fluid Mech. 742, R2.Google Scholar
Ellingsen, S. Å. 2016 Oblique waves on a vertically sheared current are rotational. Eur. J. Mech. (B/Fluids) 56, 156–160.Google Scholar
Ellingsen, S. Å. & Brevik, I 2014 How linear surface waves are affected by a current with constant vorticity. Eur. J. Phys. 35, 025005.Google Scholar
Ellingsen, S. Å & Tyvand, P. A.2015 Oscillatory point source in flow of uniform shear in three dimensions. (submitted).Google Scholar
Faltinsen, O. M. 2005 Hydrodynamics of High–Speed Marine Vehicles. Cambridge University Press.Google Scholar
Havelock, T. H. 1908 The propagation of groups of waves in dispersive media, with application to waves on water produced by a travelling disturbance. Proc. R. Soc. Lond. A 81, 398–430.Google Scholar
Havelock, T. H. 1917 Some cases of wave motion due to a submerged obstacle. Proc. R. Soc. Lond. A 520–532.Google Scholar
Havelock, T. H. 1919 Wave resistance: some cases of three-dimensional fluid motion. Proc. R. Soc. Lond. A 95, 354–365.Google Scholar
Havelock, T. H. 1922 The effect of shallow water on wave resistance. Proc. R. Soc. Lond. A 100, 499–505.Google Scholar
He, J., Zhang, C., Zhu, Y., Wu, H., Yang, C.-J., Noblesse, F., Gu, X. & Li, W. 2015 Comparison of three simple models of Kelvin’s ship wake. Eur. J. Mech. (B/Fluids) 49, 12–19.Google Scholar
Johnson, R. S. 1990 Ring waves on the surface of shear flows: a linear and nonlinear theory. J. Fluid Mech. 215, 145–160.CrossRefGoogle Scholar
Li, Y. & Ellingsen, S. Å. 2015 Initial value problems for water waves in the presence of a shear current. In Proceedings of the 25th International Offshore and Polar Engineering Conference (ISOPE), pp. 543–549.Google Scholar
Li, Y. & Ellingsen, S. Å.2016 Water waves from general, time-dependent surface pressure distribution in the presence of a shear current. Intl J. Offshore Polar Engng (in press).Google Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
McHugh, J. P. 1994 Surface waves on an inviscid shear flow in a channel. Wave Motion 19, 135–144.CrossRefGoogle Scholar
Moisy, F. & Rabaud, M. 2014 Mach-like capillary-gravity waves. Phys. Rev. E 90, 023009.Google Scholar
Munk, W. H., Scully-Power, P. & Zachariasen, F.1987 The Bakerian lecture, 1986: ships from space. Proc. R. Soc. Lond. A 412, 231–254; (1843).Google Scholar
Noblesse, F., He, J., Zhu, Y., Hong, L., Zhang, C., Zhu, R. & Yang, C. 2014 Why can ship wakes appear narrower than Kelvin’s angle? Eur. J. Mech. (B/Fluids) 46, 164–171.CrossRefGoogle Scholar
Peregrine, D. H. 1976 Interaction of water waves and currents. Adv. Appl. Mech. 16, 9–117.Google Scholar
Pethiyagoda, R, McCue, S. W. & Moroney, T. J. 2014 What is the apparent angle of a Kelvin ship wave pattern? J. Fluid Mech. 758, 468–485.CrossRefGoogle Scholar
Pethiyagoda, R, McCue, S. W. & Moroney, T. J. 2015 Wake angle for surface gravity waves on a finite depth fluid. Phys. Fluids 27, 061701.CrossRefGoogle Scholar
Rabaud, M. & Moisy, F. 2013 Ship waves: Kelvin or Mach angle? Phys. Rev. Lett. 110, 214503.Google Scholar
Raphaël, E. & de Gennes, P.-G. 1996 Capillary gravity waves caused by a moving disturbance: wave resistance. Phys. Rev. E 53, 3448–3455.CrossRefGoogle ScholarPubMed
Reed, A. M. & Milgram, J. H. 2002 Ship wakes and their radar images. Annu. Rev. Fluid Mech. 34, 469–502.Google Scholar
Thomson, Sir W. 1887 On ship waves. Proc. Inst. Mech. Engrs 38, 409–434.CrossRefGoogle Scholar
Wehausen, J. W. 1973 The wave resistance of ships. Adv. Appl. Mech. 13, 93–245.Google Scholar
Zhang, C., He, J., Zhu, Y., Yang, C.-J., Li, W., Zhu, Y., Lin, M. & Noblesse, F. 2015 Interference effects on the Kelvin wake of a monohull ship represented via a continuous distribution of sources. Eur. J. Mech. (B/Fluids) 51, 27–36.CrossRefGoogle Scholar
Zhu, Y., He, J., Zhang, C., Wu, H., Wan, D., Zhu, R. & Noblesse, F. 2015 Farfield waves created by a monohull ship in shallow water. Eur. J. Mech. (B/Fluids) 49, 226–234.Google Scholar