Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T19:15:36.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Short- to long-wave resonance and soliton formation in boundary-layer interaction with a liquid film

Published online by Cambridge University Press:  12 July 2010

M. VLACHOMITROU  and
N. PELEKASIS
M. VLACHOMITROU
Affiliation:
Department of Mechanical & Industrial Engineering, University of Thessaly, Leoforos Athinon, Pedion Areos, 38834 Volos, Greece
N. PELEKASIS*
Affiliation:
Department of Mechanical & Industrial Engineering, University of Thessaly, Leoforos Athinon, Pedion Areos, 38834 Volos, Greece
*
†Email address for correspondence: pel@uth.gr
Get access Rights & Permissions [Opens in a new window]

Abstract

Dynamic interaction between a boundary layer of air and a liquid film is investigated in this paper. The low air-to-film-viscosity ratio is considered in which case the boundary layer is quasi-steady on the time scale within which interfacial waves develop. The base flow consists of a boundary layer that drags a film of constant shear. Linear analysis, in the context of triple-deck theory, predicts the formation of a wavepacket of capillary waves that advances and spreads with time. The Froude number of de-/anti-icing fluids or water interacting with air falls well within the supercritical regime, i.e. Fr > FrCr. Numerical simulations of such flow systems were performed in the context of triple-deck theory, and they do not exhibit wave saturation or formation of uniform wavetrains. The long-term interaction is mainly dependent on film inertia as this is characterized by parameter 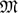= (μ/μf)2(ρf/ρ), which involves film and air viscosity and density ratios, and the dimensionless film thickness, H0, and shear, λ, provided by the base flow. Weakly nonlinear analysis taking into consideration mean drift, i.e. generation of long waves, due to self-interaction of the linear wave to O(ϵ2) in amplitude of the initial disturbance, reveals resonance between the wavepacket predicted by linear theory and long waves when the group velocity of the former happens to coincide with the phase velocity, H0λ, of long interfacial waves. Numerical simulations with anti-icing fluids and water verify this pattern. In both cases, long waves eventually dominate the dynamics and, as they are modulated with time, they lead to soliton-type structures. Anti-icing fluids eventually exhibit oscillatory spikes whose mean value never exceeds 2H0, roughly. Water films exhibit a single spike that keeps growing, thus generating a large separation bubble.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Waves/Free-surface Flows: Solitary waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 660 , 10 October 2010 , pp. 162 - 196
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bender, C. M. & Orszag., S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Benjamin, T. B. 1961 The development of three dimensional disturbances in an unstable film of liquid flowing down in an inclined plane. J. Fluid Mech. 10, 401.CrossRefGoogle Scholar
Bezos, G. M., Dunham, R. E., Genry, G. L. & Melson, W. E. 1992 Wind tunnel aerodynamic characteristics of a transport-type airfoil in a simulated heavy rain environment. Tech. Paper 3184. NASA.Google Scholar
Blennerhassett, P. J. 1980 On the generation of waves by wind. Phil. Trans. R. Soc. Lond. A 298, 451–494.Google Scholar
Brevdo, L., Laure, P., Dias, F. & Bridges, T. J. 1999 Linear pulse structure and signalling in a film flow on an inclined plane. J. Fluid Mech. 396, 37–71.CrossRefGoogle Scholar
Brotherton-Ratcliffe, R. V. & Smith, F. T. 1987 Complete breakdown of an unsteady interactive boundary layer (over a surface distortion or in a liquid layer). Mathematika 34, 86–100.CrossRefGoogle Scholar
Clamond, D. & Germain, J. P. 1999 Interaction between a Stokes wave packet and a solitary wave. Eur. J. Mech. B/Fluids 18 (1), 67–91.CrossRefGoogle Scholar
Couairon, A. & Chomaz, J. 1997 Absolute and convective instabilities, front velocities and global modes in non-linear systems. Physica D 108, 236–276.CrossRefGoogle Scholar
Craik, A. D. D. 1966 Wind generated waves in thin liquid films. J. Fluid Mech. 26 (2), 369–392.CrossRefGoogle Scholar
Craik, A. D. D. 1985 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Davey, A., Hocking, L. M. & Stewartson, K. 1974 On the nonlinear evolution of three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 63, 529–536.CrossRefGoogle Scholar
Davey, A. & Stewartson, K. 1974 On three dimensional packets of surface waves. Proc. R. Soc. Lond. A 388, 101.Google Scholar
Djordjevic, V. D. & Rdecopp, L. G. 1977 On two dimensional packets of capillary–gravity waves. J. Fluid Mech. 160, 465–498.Google Scholar
Hill, E. G. & Zierten, T. A. 1993 Aerodynamic effects of aircraft ground deicing/anti-icing fluids. J. Aircr. 30, 24.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. J. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Kachanov, Y. S., Ryzhov, O. R. & Smith, F. T. 1993 Formation of solitons in transitional boundary layers: theory and experiment. J. Fluid Mech. 251, 273–297.CrossRefGoogle Scholar
Li, L., Walker, J. D. A., Bowles, R. I. & Smith, F. T. 1998 Short-scale break-up in unsteady interactive layers: local development of normal pressure gradients and vortex wind-up. J. Fluid Mech. 374, 335–378.CrossRefGoogle Scholar
Lin, S. P. 1974 Finite amplitude side-band stability of a viscous film. J. Fluid Mech. 63 (3), 417–429.CrossRefGoogle Scholar
Ludwieg, H. & Hornung, H. 1989 The instability of a liquid film on a wall exposed to an air flow. J. Fluid Mech. 200, 217–233.CrossRefGoogle Scholar
Ma, Y.-C. & Redekopp, L. G. 1979 Some solutions pertaining to the resonant interaction of long and short waves. Phys. Fluids 22 (10), 1872–1876.CrossRefGoogle Scholar
Meza, C. E. & Balakotaiah, V. 2008 Modeling and experimental studies of large amplitude waves on vertically falling films. Chem. Engng Sci. 63, 4704–4734.CrossRefGoogle Scholar
Nelson, J. J., Alving, A. E. & Joseph, D. D. 1995 Boundary layer flow of air over water on a flat plate. J. Fluid Mech. 284, 159–169.CrossRefGoogle Scholar
Ozgen, S., Carbonaro, M. & Sarma, G. S. R. 2002 Experimental study of wave characteristics on a thin layer of de-/anti-icing fluid. Phys. Fluids 14, 3391–3402.CrossRefGoogle Scholar
Ozgen, S., Degrez, G. & Sarma, G. S. R. 1998 Two-fluid boundary layer stability. Phys. Fluids 10 (11), 2746–2757.CrossRefGoogle Scholar
Pelekasis, N. A. & Tsamopoulos, J. A. 2001 Linear stability analysis of a gas boundary layer flowing past a thin liquid film over a flat plate. J. Fluid Mech. 436, 321–352.CrossRefGoogle Scholar
Rothmayer, A. P., Matheis, B. D. & Timoshin, S. N. 2002 Thin liquid films flowing over external aerodynamic surfaces. J. Engng Math. 42, 341–357.CrossRefGoogle Scholar
Saarlos, W. & Hohenberg, P. C. 1992 Fronts, pulses, sources and sinks in generalized complex Ginzburg–Landau equations. Physica D 56, 303–367.CrossRefGoogle Scholar
Smith, F. T. 1979 Nonlinear stability of boundary layers for disturbances of various sizes. Proc. R. Soc. Lond. A 368, 573–589.Google Scholar
Smith, F. T. 1986 Two-dimensional disturbance travel, growth and spreading in boundary layers. J. Fluid Mech. 169, 353–377.CrossRefGoogle Scholar
Smith, F. T. 1988 Finite-time break-up can occur in any unsteady interacting boundary layer. Mathematika 35, 256–273.CrossRefGoogle Scholar
Smith, F. T. & Burggraf, O. R. 1985 On the development of large-sized short-scaled disturbances in boundary layers. Proc. R. Soc. Lond. A 399, 25–55.Google Scholar
Smith, F. T. & Stewart, P. A. 1987 The resonant–triad interaction in boundary-layer transition. J. Fluid Mech. 179, 227–252.CrossRefGoogle Scholar
Smyrnaios, D. N., Pelekasis, N. A. & Tsamopoulos, I. A. 2000 Boundary layer flow of air past solid surfaces in the presence of rainfall. J. Fluid Mech. 425, 79–110.CrossRefGoogle Scholar
Stewartson, K. & Stuart, J. T. 1971 A non-linear instability theory for a wave system in plane Poiseuille flow. J. Fluid Mech. 48 (3), 529–545.CrossRefGoogle Scholar
Timoshin, S. N. 1997 Instabilities in a high-Reynolds-number boundary layer on a film-coated surface. J. Fluid Mech. 353, 163–195.CrossRefGoogle Scholar
Timoshin, S. N. & Smith, F. T. 2003 Non-local interactions and feedback instability in a high Reynolds number flow. Theor. Comput. Fluid Dyn. 17, 1–18.CrossRefGoogle Scholar
Vlachomitrou, M. & Pelekasis, N. 2009 Nonlinear interaction between a boundary layer and a liquid film. J. Fluid Mech. 638, 199–242.CrossRefGoogle Scholar
Yiantsios, S. G. & Higgins, B. G. 1988 Linear stability of plane Poiseuille flow of two superposed fluids. Phys. Fluids 31, 3225.CrossRefGoogle Scholar