Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T06:58:17.616Z Has data issue: false hasContentIssue false
  • English
  • Français

Singularities in the complex physical plane for deep water waves

Published online by Cambridge University Press:  22 September 2011

Gregory R. Baker  and
Chao Xie
Gregory R. Baker*
Affiliation:
Department of Mathematics, The Ohio State University, 231 West 18th Avenue, Columbus, OH 43210, USA
Chao Xie
Affiliation:
Department of Mathematics, The Ohio State University, 231 West 18th Avenue, Columbus, OH 43210, USA
*
†Email address for correspondence: baker@math.osu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Deep water waves in two-dimensional flow can have curvature singularities on the surface profile; for example, the limiting Stokes wave has a corner of 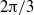radians and the limiting standing wave momentarily forms a corner of 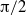radians. Much less is known about the possible formation of curvature singularities in general. A novel way of exploring this possibility is to consider the curvature as a complex function of the complex arclength variable and to seek the existence and nature of any singularities in the complex arclength plane. Highly accurate boundary integral methods produce a Fourier spectrum of the curvature that allows the identification of the nearest singularity to the real axis of the complex arclength plane. This singularity is in general a pole singularity that moves about the complex arclength plane. It approaches the real axis very closely when waves break and is associated with the high curvature at the tip of the breaking wave. The behaviour of these singularities is more complex for standing waves, where two singularities can be identified that may collide and separate. One of them approaches the real axis very closely when a standing wave forms a very narrow collapsing column of water almost under free fall. In studies so far, no singularity reaches the real axis in finite time. On the other hand, the surface elevation 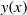has square-root singularities in the complex plane that do reach the real axis in finite time, the moment when a wave first starts to break. These singularities have a profound effect on the wave spectra.

JFM classification

Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 685 , 25 October 2011 , pp. 83 - 116
Copyright
Copyright © Cambridge University Press 2011 The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution-NonCommercial-ShareAlike licence <http://creativecommons.org/licenses/by-nc-sa/2.5/>. The written permission of Cambridge University Press must be obtained for commercial re-use.

References

1. Baker, G. R. 1983 Generalized vortex methods for free-surface flows. In Waves on Fluid Interfaces, pp. 53–81. Academic.CrossRefGoogle Scholar
2. Baker, G. R., Caflisch, R. E. & Siegel, M. 1993 Singularity formation during Rayleigh–Taylor instability. J. Fluid Mech. 252, 51–78.CrossRefGoogle Scholar
3. Baker, G., McCrory, R., Verdon, C. & Orszag, S. 1987 Rayleigh–Taylor instability of fluid layers. J. Fluid Mech. 178, 161–178.CrossRefGoogle Scholar
4. Baker, G. R., Meiron, D. I. & Orszag, S. A. 1980 Vortex simulations of the Rayleigh–Taylor instability. Phys. Fluids 23, 1485–1490.CrossRefGoogle Scholar
5. Baker, G. R., Meiron, D. I. & Orszag, S. A. 1982 Generalized vortex methods for free-surface flow problems. J. Fluid Mech. 123, 477–501.CrossRefGoogle Scholar
6. Baker, G. & Moore, D. 1989 The rise and distortion of a two-dimensional gas bubble in an inviscid liquid. Phys. Fluids A 1, 1451–1459.CrossRefGoogle Scholar
7. Baker, G. R. & Nachbin, A. 1998 Stable methods for vortex sheet motion in the presence of surface tension. SIAM J. Sci. Comput. 19, 1737–1766.CrossRefGoogle Scholar
8. Caflisch, R. E. & Orellana, O. F. 1989 Singular solutions and ill-posedness for the evolution of vortex sheets. SIAM J. Math. Anal. 20, 293–307.CrossRefGoogle Scholar
9. Caflisch, R. & Semmes, S. 1990 A nonlinear approximation for vortex sheet evolution and singularity formation. Physica D 41, 197–207.CrossRefGoogle Scholar
10. Carrier, G. F., Krook, M. & Pearson, C. E. 1966 Functions of a Complex Variable: Theory and Technique. McGraw-Hill.Google Scholar
11. Ceniceros, H. D. & Hou, T. Y. 1998 Convergence of a non-stiff boundary integral method for interfacial flows with surface tension. Maths Comput. 67, 137–182.CrossRefGoogle Scholar
12. Cowley, S. J., Baker, G. R. & Tanveer, S. A. 1999 On the formation of Moore curvature singularities in vortex sheets. J. Fluid Mech. 378, 233–267.CrossRefGoogle Scholar
13. Craig, W. & Wayne, C. E. 2007 Mathematical aspects of surface water waves. Russ. Math. Surv. 62, 453–473.CrossRefGoogle Scholar
14. Ely, J. S. & Baker, G. R. 1993 High-precision calculations of vortex sheet motion. J. Comput. Phys. 111, 275–281.CrossRefGoogle Scholar
15. Fontelos, A. & de la Hoz, F. 2010 Singularities in Water Waves and the Rayleigh–Taylor problem. J. Fluid Mech. 651, 211–239.CrossRefGoogle Scholar
16. Galassi, M., Davies, J., Theiler, J., Gough, B., Jungman, G., Alken, P., Booth, M. & Rossi, F. 2009 Nonlinear least-squares fitting. In GNU Scientific Library Reference Manual, pp. 403–414.Google Scholar
17. Germain, P., Masmoudi, N. & Shatah, J. 2009 Global solutions for the gravity water waves equation in dimension 3. C. R. Acad. Sci. Paris (I) 346, 897–902.CrossRefGoogle Scholar
18. Gottlieb, D. & Orszag, S. A. 1977 Numerical Analysis of Spectral Methods: Theory and Applications, CBMS-NSF Regional Conference Series in Applied Mathematics . SIAM.CrossRefGoogle Scholar
19. Hou, T. Y. & Hu, G. 2003 Singularity formation in three-dimensional vortex sheets. Phys. Fluids 15, 147–172.CrossRefGoogle Scholar
20. Hou, T. Y., Lowengrub, J. S. & Shelley, M. J. 1994 Removing the stiffness from interfacial flows with surface tension. J. Comput. Phys. 114, 312–338.CrossRefGoogle Scholar
21. Ishihara, T. & Kaneda, Y. 1994 Spontaneous singularity formation in the shape of vortex sheet in three-dimensional flow. J. Phys. Soc. Japan 63, 388–392.CrossRefGoogle Scholar
22. Kano, T. & Nishida, T. 1979 Sur les ondes de surface de l’eau avec une justification mathématique des equations des ondes en eau peu profonde. J. Maths Kyoto Univ. 19, 335–370.Google Scholar
23. Krasny, R. 1986 A study of singularity formation in a vortex sheet by the point-vortex approximation. J. Fluid Mech. 167, 65–93.CrossRefGoogle Scholar
24. Kuznetsov, E. A., Spector, M. D. & Zakharov, V. E. 1994 Formation of singularities on the free surface of an ideal fluid. Phys. Rev. E 49 (2), 1283–1290.CrossRefGoogle ScholarPubMed
25. Longuet-Higgins, M. 1972 A class of exact, time-dependent, free-surface flows. J. Fluid Mech. 55, 529–543.CrossRefGoogle Scholar
26. Longuet-Higgins, M. 1980 On the forming of sharp corners at a free surface. Proc. R. Soc. Lond. A 371, 453–478.Google Scholar
27. Longuet-Higgins, M. 1982 Parametric solutions for breaking waves. J. Fluid Mech. 121, 403–424.CrossRefGoogle Scholar
28. Longuet-Higgins, M. & Dommermuth, D. 2001 On the breaking of standing waves by falling jets. Phys. Fluids 13, 1652–1659.CrossRefGoogle Scholar
29. Mercer, G. N. & Roberts, A. J. 1992 Standing waves in deep water. Their stability and extreme form. Phys. Fluids A 4, 259–269.CrossRefGoogle Scholar
30. Moore, D. W. 1979 The spontaneous appearance of a singularity in the shape of an evolving vortex sheet. Proc. R. Soc. Lond. A 365, 105–119.Google Scholar
31. Nie, Q. & Baker, G. 1998 Application of adaptive quadrature to axi-symmetric vortex sheet motion. J. Comput. Phys. 143, 49–69.CrossRefGoogle Scholar
32. Okamura, M. 1998 On the enclosed crest angle of the limiting profile of standing waves. Wave Motion 28, 79–87.CrossRefGoogle Scholar
33. Penny, W. G. & Price, A. T. 1952 Finite periodic stationary gravity waves in a perfect fluid. Phil. Trans. R. Soc. Lond. 244, 254–284.Google Scholar
34. Shelley, M. J. 1992 A study of singularity formation in vortex-sheet motion by a spectrally accurate vortex method. J. Fluid Mech. 244, 493–526.CrossRefGoogle Scholar
35. Shinbrot, M. 1976 The initial value problem for surface waves under gravity. Indiana Univ. Math. J. 25, 281–300.CrossRefGoogle Scholar
36. Sulem, C., Sulem, P.-L. & Frisch, H. 1983 Tracing complex singularities with spectral methods. J. Comput. Phys. 50, 138–161.CrossRefGoogle Scholar
37. Tanveer, S. A. 1991 Singularities in water waves and Rayleigh–Taylor instability. Proc. R. Soc. Lond. A 435, 137–158.Google Scholar
38. Tanveer, S. A. 1993 Singularities in the classical Rayleigh–Taylor flow: formation and subsequent motion. Proc. R. Soc. Lond. A 441, 501–525.Google Scholar
39. Toland, J. 1996 Stokes waves. Topol. Meth. Nonlinear Anal. 7, 1–48.CrossRefGoogle Scholar
40. Vichnevetsky, R. & Bowles, J. B. 1982 Fourier Analysis of Numerical Approximations of Hyperbolic Equations. SIAM Studies in Applied Mathematics.CrossRefGoogle Scholar
41. Wu, S. 1997 Well-posedness in Sobolev spaces of the full water wave problem in 2-D. Invent. Math. 130, 39–72.CrossRefGoogle Scholar
42. Wu, S. 1999 Well-posedness in Sobolev spaces of the full water wave problem in 3-D. J. Am. Math. Soc. 12, 445–495.CrossRefGoogle Scholar
43. Wu, S. 2009 Almost global wellposedness of the 2-D full water water problem. Invent. Math. 177, 45–135.CrossRefGoogle Scholar