Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T06:38:23.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Small-scale anisotropy in turbulent boundary layers

Published online by Cambridge University Press:  31 August 2016

Alain Pumir ,
Haitao Xu  and
Eric D. Siggia
Alain Pumir*
Affiliation:
Univ Lyon, Ecole Normale Supérieure de Lyon, Univ Claude Bernard, CNRS, Laboratoire de Physique, F-69342, Lyon, France Max-Planck Institute for Dynamics and Self-Organisation, Göttingen, D-37077, Germany
Haitao Xu
Affiliation:
Center for Combustion Energy and Department of Thermal Engineering, Tsinghua University, 100084, Beijing, China Max-Planck Institute for Dynamics and Self-Organisation, Göttingen, D-37077, Germany
Eric D. Siggia
Affiliation:
Center for Physics and Biology, Rockefeller University, New York, NY 10065, USA
*
†Email address for correspondence: alain.pumir@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In a channel flow, the velocity fluctuations are inhomogeneous and anisotropic. Yet, the small-scale properties of the flow are expected to behave in an isotropic manner in the very-large-Reynolds-number limit. We consider the statistical properties of small-scale velocity fluctuations in a turbulent channel flow at moderately high Reynolds number (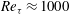$Re_{\unicode[STIX]{x1D70F}}\approx 1000$), using the Johns Hopkins University Turbulence Database. Away from the wall, in the logarithmic layer, the skewness of the normal derivative of the streamwise velocity fluctuation is approximately constant, of order 1, while the Reynolds number based on the Taylor scale is 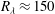$R_{\unicode[STIX]{x1D706}}\approx 150$. This defines a small-scale anisotropy that is stronger than in turbulent homogeneous shear flows at comparable values of 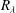$R_{\unicode[STIX]{x1D706}}$. In contrast, the vorticity–strain correlations that characterize homogeneous isotropic turbulence are nearly unchanged in channel flow even though they do vary with distance from the wall with an exponent that can be inferred from the local dissipation. Our results demonstrate that the statistical properties of the fluctuating velocity gradient in turbulent channel flow are characterized, on one hand, by observables that are insensitive to the anisotropy, and behave as in homogeneous isotropic flows, and on the other hand by quantities that are much more sensitive to the anisotropy. How this seemingly contradictory situation emerges from the simultaneous action of the flux of energy to small scales and the transport of momentum away from the wall remains to be elucidated.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 5 - 23
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, M., Antonia, R. A. & Kawamura, H. 2009 Correlation between scall-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.CrossRefGoogle Scholar
Antonia, R. A., Abe, H. & Kawamura, H. 2009 Analogy between velocity and scalar fields in turbulent channel flow. J. Fluid Mech. 628, 241–268.Google Scholar
Ashurst, W. M., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain in simulated Navier–Stokes turbulence. Phys. Fluids 30, 2343–2353.Google Scholar
Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1, 497–504.Google Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414, 43–164.Google Scholar
Biferale, L. & Vergassola, M. 2001 Isotropy versus anisotropy in small-scale turbulence. Phys. Fluids 13, 2139–2141.Google Scholar
Bradshaw, P. & Perot, B. 1993 A note on turbulent energy dissipation in the viscous wall region. Phys. Fluids 5, 3305–3306.Google Scholar
Brouwers, J. J. H. 2007 Dissipation equals production in the log layer of wall-induced turbulence. Phys. Fluids 19, 101702.Google Scholar
Cardesa, J. I., Mistry, D., Gan, L. & Dawson, J. R. 2013 Invariants of the reduced velocity gradient tensor in turbulent flows. J. Fluid Mech. 716, 597–615.Google Scholar
Cardesa, J. I., Vela-Martin, A., Dong, S. & Jimenez, J. 2015 The temporal evolution of the energy flux across scales in homogeneous turbulence. Phys. Fluids 27, 111702.Google Scholar
Casciola, C. M., Gualtieri, P., Benzi, R. & Piva, R. 2003 Scale-by-scale budget and similarity laws for shear turbulence. J. Fluid Mech. 476, 105–114.Google Scholar
Casciola, C. M., Gualtieri, P., Jacob, B. & Piva, R. 2007 The residual anisotropy at small scales in high shear turbulence. Phys. Fluids 19, 101704.Google Scholar
Corrsin, S. L.1958 Local isotropy in turbulent shear flows. Tech. Rep. National Advisory Committee for Aeronautics.Google Scholar
Dong, S.2016 Coherent structures in statistically-stationary homogeneous shear turbulence. PhD thesis, Universidad Politécnica de Madrid.Google Scholar
Dong, S., Lozano-Durán, A., Sekimoto, A. & Jimenez, J.2015 Detached coherent structures in channel revisited: comparison with homogeneous shear turbulence. Abstract, 15th European Turbulence Conference. http://www.etc15.nl/proceedings/proceedings/documents/286.pdf.Google Scholar
Falkovich, G., Gawedzki, K. & Vergassola, M. 2001 Particles and fields in fluid turbulence. Rev. Mod. Phys. 73, 913–975.Google Scholar
Ferchichi, M. & Tavoularis, S. 2000 Reynolds number effects on the fine structure of uniformly sheared turbulence. Phys. Fluids 11, 2942–2953.Google Scholar
Frisch, U. 1995 Turbulence, 1st edn. Cambridge University Press.Google Scholar
Garg, S. & Warhaft, Z. 1998 On small scale statistics in a simple shear flow. Phys. Fluids 10, 662–673.CrossRefGoogle Scholar
Graham, J., Lee, M., Malaya, N., Moser, R. D., Eyink, G. & Meneveau, C.2014 The JHU turbulence database: turbulent channel flow data set. http://turbulence.pha.jhu.edu/docs/README-CHANNEL.pdf.Google Scholar
Gualtieri, P., Casciola, C. M., Benzi, R., Amati, G. & Piva, R. 2002 Scaling laws and intermittency in homogeneous shear flow. Phys. Fluids 14, 583–596.CrossRefGoogle Scholar
Head, M. R. & Bandyopadhyay, P. 1991 New aspects of turbulent boundary layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Holzer, M. & Siggia, E. D. 1994 Turbulent mixing of a passive scalar. Phys. Fluids 6, 1820–1837.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.Google Scholar
Ishihara, T., Yoshida, K. & Kaneda, Y. 2002 Anisotropic velocity correlation spectrum at small scales in a homogeneous turbulent shear flow. Phys. Rev. Lett. 88, 154501.CrossRefGoogle Scholar
Kaneda, Y., Morishita, K. & Ishihara, T.2013 Small scale universality and spectral characteristics in turbulent flows. In International Symposium on Turbulence and Shear Flow Phenomena. http://www.tsfp-conference.org/proceedings/2013/v1/inv2.pdf.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds numbers. J. Fluid Mech. 177, 133–166.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kurien, S. & Sreenivasan, K. R. 2000 Anisotropic scaling contribution to high-order structure functions in high-Reynolds-number turbulence. Phys. Rev. E 62, 2206–2212.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics, 1st edn. Pergamon.Google Scholar
Lee, M., Malaya, N. & Moser, R.2013 Petascale direct numerical simulation of turbulent chennel flow on up to 768k cores. Supercomputing (SC13). https://www.hpcwire.com/2013/11/15/sc13-research-highlight-petascale-dns-turbulent-channel-flow/.Google Scholar
Li, Y., Wan, M., Yang, Y., Burns, R., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and application to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 9 (31), 133–166.Google Scholar
Lumley, J. L. 1967 Similarity and the turbulent energy spectrum. Phys. Fluids 10, 855–858.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3,1–11.Google Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flows. J. Fluid Mech. 118, 341–377.Google Scholar
Moin, P. & Kim, J. 1985 The structure of the vorticity field in turbulent channel flow. Part 1. Analysis of instantaneous fields and statistical correlations. J. Fluid Mech. 155, 441–464.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flows up to r 𝜏 = 590. Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
Mydlarski, L., Pumir, A., Shraiman, B., Siggia, E. D. & Warhaft, Z. 1998 Structures and multipoint correlators for turbulent advection: predictions and experiments. Phys. Rev. Lett. 81, 4373–4376.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pumir, A. 1994 A numerical study of the mixing of a passive scalar in three-dimensions in the presence of a mean gradient. Phys. Fluids 6, 2118–2132.Google Scholar
Pumir, A. 1996 Turbulence in homogeneous shear flows. Phys. Fluids 8, 3112–3127.Google Scholar
Pumir, A. 1998 Structures of the three-point correlation function of a passive scalar in the presence of a mean gradient. Phys. Rev. E 57, 2914–2929.Google Scholar
Pumir, A. & Shraiman, B. 1995 Persistent small scale anisotropy in homogeneous shear flows. Phys Rev. Lett. 75, 3114–3117.Google Scholar
Saddoughi, S. & Veeravalli, S. V. 1994 On small scale statistics in a simple shear flow. J. Fluid Mech. 268, 333–372.Google Scholar
Schumacher, J. & Eckhardt, B. 2000 On statistically stationary homogeneous shear turbulence. Eur. Phys. Lett. 52, 627–632.Google Scholar
Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2003 Derivative moments in turbulent shear flows. Phys. Fluids 15, 84–90.Google Scholar
Sekimoto, A., Dong, S. & Jimenez, J.2016 Numerical simulation of statistically stationary and homogeneous shear turbulence and its relation to other shear flows. arXiv:1601.01646.Google Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number (R 𝜆 = 1000) turbulent shear flow. Phys. Fluids 12, 2976–2989.Google Scholar
Shraiman, B. & Siggia, E. D. 2000 Scalar turbulence. Nature 405, 639–646.Google Scholar
Siggia, E. D. 1981 Invariants for the one-point vorticity and strain rate correlation functions. Phys. Fluids 24, 1934–1936.Google Scholar
Smits, A. J. 2010 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Sreenivasan, K. R. 1991 On local isotropy of passive scalars in turbulent flows. Proc. R. Soc. Lond. A 434, 165–182.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Staicu, A., Vorselaars, B. & van de Water, W. 2003 Turbulence anisotropy and the SO (3) description. Phys. Rev. E 68, 046303.Google Scholar
Tennekes, H. & Lumley, J. L. 1983 A First Course on Turbulence, 9th edn. MIT Press.Google Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In 2nd Midwestern Conference Fluid Mechanics, pp. 1–19. Columbus Ohio State University.Google Scholar
Tong, C. & Warhaft, Z. 1994 On passive scalar derivative statisics in grid turbulence. Phys. Fluids 6, 2165–2176.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence, 1st edn. Springer.Google Scholar
Tsuji, Y. 2003 Large-scale anisotropy effect on small-scale statistics over rough wall turbulent boundary layers. Phys. Fluids 15, 3816–3828.Google Scholar
Vreman, A. W. & Kuerten, J. G. M. 2014 Statistics of spatial derivatives of velocity and pressure in turbulent channel flow. Phys. Fluids 27, 084103.Google Scholar
Wallace, J. M. 2009 Twenty years of experimental and direct numerical simulation access to the velocity gradient tensor: what have we learned about turbulence? Phys. Fluids 21, 021301.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.Google Scholar
Warhaft, Z. & Shen, X. 2001 Some comments on the small scale structure of turbulence at high Reynolds numbers. Phys. Fluids 13, 1532–1533.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 4–41.Google Scholar