Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T03:58:19.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Small-scale dynamics of settling, bidisperse particles in turbulence

Published online by Cambridge University Press:  02 February 2018

Rohit Dhariwal Open the ORCID record for Rohit Dhariwal [Opens in a new window]  and
Andrew D. Bragg Open the ORCID record for Andrew D. Bragg [Opens in a new window]
Rohit Dhariwal
Affiliation:
Department of Civil and Environmental Engineering, Duke University, Durham, NC 27708, USA
Andrew D. Bragg*
Affiliation:
Department of Civil and Environmental Engineering, Duke University, Durham, NC 27708, USA
*
†Email address for correspondence: andrew.bragg@duke.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Mixing and collisions of inertial particles at the small scales of turbulence can be investigated by considering how pairs of particles move relative to each other. In real problems the two particles will have different sizes, i.e. they are bidisperse, and the effect of gravity on their motion is often important. However, how turbulence and gravity compete to control the motion of bidisperse inertial particles is poorly understood. Motivated by this, we use direct numerical simulations (DNS) to investigate the dynamics of settling, bidisperse particles in isotropic turbulence. In agreement with previous studies, we find that without gravity (i.e. 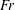$Fr=\infty$, where $Fr$ is the Froude number), bidispersity leads to an enhancement of the relative velocities, and a suppression of their spatial clustering. For 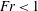$Fr<1$, the relative velocities in the direction of gravity are enhanced by the differential settling velocities of the bidisperse particles, as expected. However, we also find that gravity can strongly enhance the relative velocities in the ‘horizontal’ directions (i.e. in the plane normal to gravity). This non-trivial behaviour occurs because fast settling particles experience rapid fluctuations in the fluid velocity field along their trajectory, leading to enhanced particle accelerations and relative velocities. Indeed, the results show that even when 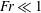$Fr\ll 1$, turbulence can still play an important role, not only on the horizontal motion, but also on the vertical motion of the particles. This is related to the fact that 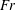$Fr$ only characterizes the importance of gravity compared with some typical acceleration of the fluid, yet accelerations in turbulence are highly intermittent. As a consequence, there is a significant probability for particles to be in regions of the flow where the Froude number based on the local, instantaneous fluid acceleration is 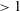${>}1$, even though the typically defined Froude number is 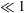$\ll 1$. This could imply, for example, that extreme events in the mixing of settling, bidisperse particles are only weakly affected by gravity even when 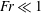$Fr\ll 1$. We also find that gravity drastically reduces the clustering of bidisperse particles. These results are strikingly different to the monodisperse case, for which recent results have shown that when 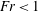$Fr<1$, gravity strongly suppresses the relative velocities in all directions, and can enhance clustering. Finally, we consider the implications of these results for the collision rates of settling, bidisperse particles in turbulence. We find that for 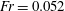$Fr=0.052$, the collision kernel is almost perfectly predicted by the collision kernel for bidisperse particles settling in quiescent flow, such that the effect of turbulence may be ignored. However, for 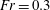$Fr=0.3$, turbulence plays an important role, and the collisions are only dominated by gravitational settling when the difference in the particle Stokes numbers is 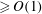${\geqslant}O(1)$.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 839 , 25 March 2018 , pp. 594 - 620
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ayala, O., Rosa, B., Wang, L.-P. & Grabowski, W. W. 2008 Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 1. Results from direct numerical simulation. New J. Phys. 10, 075015.CrossRefGoogle Scholar
Ayyalasomayajula, S., Warhaft, Z. & Collins, L. R. 2008 Modeling inertial particle acceleration statistics in isotropic turbulence. Phys. Fluids 20, 094104.Google Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A. S., Musacchio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550, 349–358.CrossRefGoogle Scholar
Bec, J., Biferale, L., Cencini, M., Lanotte, A. S. & Toschi, F. 2010 Intermittency in the velocity distribution of heavy particles in turbulence. J. Fluid Mech. 646, 527–536.Google Scholar
Bec, J., Homann, H. & Ray, S. S. 2014 Gravity-driven enhancement of heavy particle clustering in turbulent flow. Phys. Rev. Lett. 112, 184501.Google Scholar
Bragg, A. D. 2017 Developments and difficulties in predicting the relative velocities of inertial particles at the small-scales of turbulence. Phys. Fluids 29 (4), 043301.Google Scholar
Bragg, A. D. & Collins, L. R. 2014a New insights from comparing statistical theories for inertial particles in turbulence. Part I. Spatial distribution of particles. New J. Phys. 16, 055013.Google Scholar
Bragg, A. D. & Collins, L. R. 2014b New insights from comparing statistical theories for inertial particles in turbulence. Part II. Relative velocities of particles. New J. Phys. 16, 055014.Google Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2015a Mechanisms for the clustering of inertial particles in the inertial range of isotropic turbulence. Phys. Rev. E 92, 023029.Google ScholarPubMed
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2015b On the relationship between the non-local clustering mechanism and preferential concentration. J. Fluid Mech. 780, 327–343.Google Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2016 Forward and backward in time dispersion of fluid and inertial particles in isotropic turbulence. Phys. Fluids 28 (1), 013305.Google Scholar
Chang, K., Malec, B. J. & Shaw, R. A. 2015 Turbulent pair dispersion in the presence of gravity. New J. Phys. 17 (3), 033010.Google Scholar
Chen, J. & Jin, G. 2017 Large-eddy simulation of turbulent preferential concentration and collision of bidisperse heavy particles in isotropic turbulence. Powder Technol. 314, 281–290.Google Scholar
Chun, J., Koch, D. L., Rani, S., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.Google Scholar
Cuzzi, J. N., Dobrovolskis, A. R. & Hogan, R. C. 1996 Turbulence, chondrules, and planetesimals. In Chondrules and the Protoplanetary Disk (ed. Hewins, R. H., Jones, R. H. & Scott, E. R. D.), pp. 35–43. Cambridge University Press.Google Scholar
De Lillo, F., Cencini, M., Durham, W. M., Barry, M., Stocker, R., Climent, E. & Boffetta, G. 2014 Turbulent fluid acceleration generates clusters of gyrotactic microorganisms. Phys. Rev. Lett. 112, 044502.Google Scholar
Devenish, B. J., Bartello, P., Brenguier, J.-L., Collins, L. R., Grabowski, W. W., Ijzermans, R. H. A., Malinowski, S. P., Reeks, M. W., Vassilicos, J. C., Wang, L.-P. et al. 2012 Droplet growth in warm turbulent clouds. Q. J. R. Meteorol. Soc. 138, 1401–1429.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Faeth, G. M. 1996 Spray combustion phenomena. Int. Combust. Symp. 26 (1), 1593–1612.Google Scholar
Grabowski, W. W. & Wang, L.-P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45, 293–324.Google Scholar
Gustavsson, K. & Mehlig, B. 2011 Distribution of relative velocities in turbulent aerosols. Phys. Rev. E 84, 045304.Google ScholarPubMed
Gustavsson, K., Vajedi, S. & Mehlig, B. 2014 Clustering of particles falling in a turbulent flow. Phys. Rev. Lett. 112, 214501.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016a The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 796, 617–658.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016b The effect of reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects. J. Fluid Mech. 796, 659–711.Google Scholar
Ireland, P. J., Vaithianathan, T., Sukheswalla, P. S., Ray, B. & Collins, L. R. 2013 Highly parallel particle-laden flow solver for turbulence research. Comput. Fluids 76, 170–177.Google Scholar
Johansen, A., Oishi, J. S., Mac Low, M. M., Klahr, H. & Henning, T. 2007 Rapid planetesimal formation in turbulent circumstellar disks. Nature 448 (7157), 1022–1025.Google Scholar
Jonas, P. R. 1996 Turbulence and cloud microphysics. Atmos. Res. 40 (2), 283–306.Google Scholar
Kruis, F. E. & Kusters, K. A. 1997 The collision rate of particles in turbulent flow. Chem. Engng Commun. 158, 201–230.Google Scholar
Li, W. I., Perzl, M., Heyder, J., Langer, R., Brain, J. D., Englemeier, K. H., Niven, R. W. & Edwards, D. A. 1996 Aerodynamics and aerosol particle deaggregation phenomena in model oral–pharyngeal cavities. J. Aero. Sci. 27 (8), 1269–1286.Google Scholar
Lu, J., Nordsiek, H. & Shaw, R. A. 2010 Clustering of settling charged particles in turbulence: theory and experiments. New J. Phys. 12 (12), 123030.Google Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.CrossRefGoogle Scholar
McQuarrie, D. A. 1976 Statistical Mechanics. Harper & Row.Google Scholar
Moody, E. G. & Collins, L. R. 2003 Effect of mixing on nucleation and growth of titania particles. Aerosol Sci. Tech. 37, 403–424.Google Scholar
Pan, L. & Padoan, P. 2010 Relative velocity of inertial particles in turbulent flows. J. Fluid Mech. 661, 73–107.Google Scholar
Pan, L. & Padoan, P. 2014 Turbulence-induced relative velocity of dust particles. Part IV. The collision kernel. Astrophys. J. 797 (2), 101.Google Scholar
Pan, L., Padoan, P. & Scalo, J. 2014a Turbulence-induced relative velocity of dust particles. Part II. The bidisperse case. Astrophys. J. 791 (1), 48.Google Scholar
Pan, L., Padoan, P. & Scalo, J. 2014b Turbulence-induced relative velocity of dust particles. Part III. The probability distribution. Astrophys. J. 792 (1), 69.CrossRefGoogle Scholar
Pan, L., Padoan, P., Scalo, J., Kritsuk, A. G. & Norman, M. L. 2011 Turbulent clustering of protoplanetary dust and planetesimal formation. Astrophys. J. 740, 6.Google Scholar
Parishani, H., Ayala, O., Rosa, B., Wang, L.-P. & Grabowski, W. W. 2015 Effects of gravity on the acceleration and pair statistics of inertial particles in homogeneous isotropic turbulence. Phys. Fluids 27 (3), 033304.Google Scholar
Pinsky, M. B., Khain, A. P. & Shapiro, M. 2007 Collisions of cloud droplets in a turbulent flow. Part IV. Droplet hydrodynamic interaction. J. Atmos. Sci. 64, 2462–2482.Google Scholar
Pruppacher, H. R. & Klett, J. D. 1997 Microphysics of Clouds and Precipitation. Kluwer.Google Scholar
Pumir, A. & Wilkinson, M. 2016 Collisional aggregation due to turbulence. Ann. Rev. Condens. Matter Phys. 7 (1), 141–170.Google Scholar
Salazar, J. P. L. C. & Collins, L. R. 2009 Two-particle dispersion in isotropic turbulent flows. Annu. Rev. Fluid Mech. 41, 405–432.Google Scholar
Salazar, J. P. L. C. & Collins, L. R. 2012a Inertial particle acceleration statistics in turbulence: effects of filtering, biased sampling and flow topology. Phys. Fluids 24, 083302.CrossRefGoogle Scholar
Salazar, J. P. L. C. & Collins, L. R. 2012b Inertial particle relative velocity statistics in homogeneous isotropic turbulence. J. Fluid Mech. 696, 45–66.Google Scholar
Shaw, R. A. 2003 Particle–turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35, 183–227.Google Scholar
Siebert, H., Gerashchenko, S., Gylfason, A., Lehmann, K., Collins, L. R., Shaw, R. A. & Warhaft, Z. 2010a Towards understanding the role of turbulence on droplets in clouds: in situ and laboratory measurements. Atmos. Res. 97 (4), 426–437.Google Scholar
Siebert, H., Shaw, R. A., Ditas, J., Schmeissner, T., Malinowski, S. P., Bodenschatz, E. & Xu, H. 2015 High-resolution measurement of cloud microphysics and turbulence at a mountaintop station. Atmos. Meas. Tech. 8 (8), 3219–3228.Google Scholar
Siebert, H., Shaw, R. A. & Warhaft, Z. 2010b Statistics of small scale velocity fluctuations in marine stratocumulus clouds. J. Atmos. Sci. 67, 262–273.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3, 1169–1178.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic, particle-laden turbulent suspension. Part I. Direct numerical simulations. J. Fluid Mech. 335, 75–109.Google Scholar
Vaillancourt, P. A. & Yau, M. K. 2000 Review of particle–turbulence interactions and consequences for cloud physics. Bull. Am. Meteorol. Soc. 81, 285–298.Google Scholar
Wang, L. P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.CrossRefGoogle Scholar
Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71, 186–192.Google Scholar
Witkowska, A., Brasseur, J. G. & Juvé, D. 1997 Numerical study of noise from isotropic turbulence. J. Comput. Acoust. 5, 317–336.Google Scholar
Woittiez, E. J., Jonker, H. J. & Portela, L. M. 2009 On the combined effects of turbulence and gravity on droplet collisions in clouds: a numerical study. J. Atmos. Sci. 66 (7), 1926–1943.Google Scholar
Zaichik, L. I., Fede, P., Simonin, O. & Alipchenkov, V. M. 2009 Statistical models for predicting the effect of bidisperse particle collisions on particle velocities and stresses in homogeneous anisotropic turbulent flows. Intl J. Multiphase Flow 35, 868–878.Google Scholar
Zaichik, L. I., Simonin, O. & Alipchenkov, V. M. 2006 Collision rates of bidisperse inertial particles in isotropic turbulence. Phys. Fluids 18, 035110.CrossRefGoogle Scholar
Zhou, Y., Wexler, A. S. & Wang, L.-P. 2001 Modelling turbulent collision of bidisperse inertial particles. J. Fluid Mech. 433, 77–104.Google Scholar