Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T07:38:37.281Z Has data issue: false hasContentIssue false
  • English
  • Français

Small-scale reconstruction in three-dimensional Kolmogorov flows using four-dimensional variational data assimilation

Published online by Cambridge University Press:  18 December 2019

Yi Li Open the ORCID record for Yi Li [Opens in a new window] ,
Jianlei Zhang ,
Gang Dong  and
Naseer S. Abdullah
Yi Li*
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK
Jianlei Zhang
Affiliation:
National Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, PR China
Gang Dong
Affiliation:
National Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, PR China
Naseer S. Abdullah
Affiliation:
School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK
*
†Email address for correspondence: yili@sheffield.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

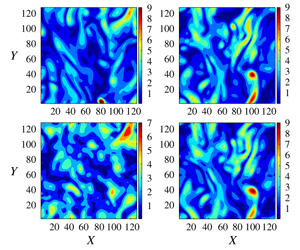
Significant insights in computational fluid dynamics have been obtained in recent years by adopting the data assimilation methods developed in the meteorology community. We apply the four-dimensional variational method to reconstruct the small scales of three-dimensional turbulent velocity fields with a moderate Reynolds number, given a time sequence of measurement data on a coarse set of grid points. The problem presents new challenges because the evolution of the flow is dominated by the nonlinear vortex stretching and the energy cascade process, which are absent from two-dimensional flows. The results show that, reconstruction is successful when the resolution of the measurement data, given in terms of the wavenumber, is of the order of the threshold value $k_{c}=0.2\unicode[STIX]{x1D702}_{K}^{-1}$, where $\unicode[STIX]{x1D702}_{K}$ is the Kolmogorov length scale of the flow. When the data are available over a period of one large eddy turnover time scale, the filtered enstrophy and other small-scale quantities are reconstructed with a 30 % or smaller normalized pointwise error, and a 90 % pointwise correlation. The spectral correlation between the reconstructed and target fields is higher than 80 % for all wavenumbers. Minimum volume enclosing ellipsoids (MVEEs) and MVEE trees are introduced to quantitatively compare the geometry of non-local structures. Results show that, for the majority samples, errors in the locations and the sizes of the reconstructed structures are within 15 %, and those in the orientations are within $15^{\circ }$. Overall, for this flow, satisfactory reconstruction of the scales two or more octaves smaller is possible if data at large scales are available for at least one large eddy turnover time. In comparison, a direct substitution scheme results in three times bigger pointwise discrepancy in enstrophy. The spectral difference between the reconstructed and target velocity fields is more than ten times higher than what is obtained with the four-dimensional variational method. The results show that further investigation is warranted to verify the efficacy of the method in flows with higher Reynolds numbers.

JFM classification

Mathematical Foundations: Computational methods Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A9
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artana, G., Cammilleri, A., Carlier, J. & Memin, E. 2012 Strong and weak constraint variational assimilations for reduced order fluid flow modeling. J. Comput. Phys. 231, 3264–3288.CrossRefGoogle Scholar
Bermejo-Moreno, I. & Pullin, D. I. 2008 On the non-local geometry of turbulence. J. Fluid Mech. 603, 101–135.CrossRefGoogle Scholar
Bewley, T. R. & Protas, B. 2004 Skin friction and pressure: the ‘footprints’ of turbulence. Physica D 196, 28–44.Google Scholar
Borue, V. & Orszag, S. A. 1996 Numerical study of three-dimensional Kolmogorov flow at high Reynolds numbers. J. Fluid Mech. 306, 293–323.CrossRefGoogle Scholar
Boyd, S. & Vandenberghe, L. 2004 Convex Optimization. Cambridge University Press.CrossRefGoogle Scholar
Brown, R. G. & Hwang, P. Y. C. 2012 Introduction to Random Signals and Applied Kalman Filtering: with MATLAB Exercises. John Wiley & Sons.Google Scholar
Cantwell, B. J. 1992 Exact solution of a restricted Euler equation for the velocity gradient tensor. Phys. Fluids A 4, 782–793.CrossRefGoogle Scholar
Chevalier, M., Hoepffner, J., Bewley, T. R. & Henningson, D. S. 2006 State estimation in wall-bounded flow systems. Part 2. Turbulent flows. J. Fluid Mech. 552, 167–187.CrossRefGoogle Scholar
Colburn, C. H., Cessna, J. B. & Bewley, T. R. 2011 State estimation in wall-bounded flow systems. Part 3. The ensemble Kalman filter. J. Fluid Mech. 682, 289–303.CrossRefGoogle Scholar
Combes, B., Heitz, D., Guibert, A. & Memin, E. 2015 A particle filter to reconstruct a free-surface flow from a depth camera. Fluid Dyn. Res. 47, 051404.CrossRefGoogle Scholar
Courtier, P., Derber, J., Errico, R., Louis, J.-F. & Vukicevic, T. 1993 Important literature on the use of adjoint, variational methods and the Kalman filter in meteorology. Tellus 45A, 342–357.CrossRefGoogle Scholar
D’adamo, J., Papadakis, N., Memin, E. & Artana, G. 2007 Variational assimilation of pod low-order dynamical systems. J. Turbul. 8, N9.Google Scholar
Ester, M., Kriegel, H.-P., Sander, J. & Xu, X. 1996 A density-based algorithm for discovering clusters in large spatial databases with noise. KDD-96 Proc. 1, 226–231.Google Scholar
Evensen, G. 2009 The ensemble Kalman filter for combined state and parameter estimation. IEEE Control Syst. Magazine 29, 83–104.CrossRefGoogle Scholar
Foures, D. P. G., Dovetta, N., Sipp, D. & Schmid, P. J. 2014 A data-assimilation method for Reynolds-averaged Navier–Stokes-driven mean flow reconstruction. J. Fluid Mech. 759, 404–431.CrossRefGoogle Scholar
Gronskis, A., Heitz, D. & Memin, E. 2013 Inflow and initial conditions for direct numerical simulation based on adjoint data assimilation. J. Comput. Phys. 242, 480–497.CrossRefGoogle Scholar
Hayase, T. 2015 Numerical simulation of real-world flows. Fluid Dyn. Res. 47, 051201.CrossRefGoogle Scholar
Heitz, D., Memin, E. & Schnorr, C. 2010 Variational fluid flow measurements from image sequences: synopsis and perspectives. Exp. Fluids 48, 369–393.CrossRefGoogle Scholar
Horiuti, K. 2003 Roles of non-aligned eigenvectors of strain-rate and subgrid-scale stress tensors in turbulence generation. J. Fluid Mech. 491, 65–100.CrossRefGoogle Scholar
Kalman, R. E. 1960 A new approach to linear filtering and prediction problems. J. Basic Engng 82 (1), 35–45.CrossRefGoogle Scholar
Kalnay, E. 2003 Atmospheric Modelling, Data Assimilation and Predictability. Cambridge University Press.Google Scholar
Kang, H. S. & Meneveau, C. 2005 Effect of large-scale coherent structures on subgrid-scale stress and strain-rate eigenvector alignments in turbulent shear flow. Phys. Fluids 17, 055103.CrossRefGoogle Scholar
Kato, H. & Obayashi, S. 2013 Approach for uncertainty of turbulence modeling based on data assimilation technique. Comput. Fluids 85, 2–7.CrossRefGoogle Scholar
Kato, H., Yoshizawa, A., Ueno, C. & Obayashi, S. 2015 A data assimilation methodology for reconstructing turbulent flows around aircraft. J. Comput. Phys. 283, 559–581.CrossRefGoogle Scholar
Khachiyan, L. G. 1996 Rounding of polytopes in the real number model of computation. Math. Oper. Res. 21, 307–320.CrossRefGoogle Scholar
Lalescu, C. C., Meneveau, C. & Eyink, G. L. 2013 Synchronization of chaos in fully developed turbulence. Phys. Rev. Lett. 110, 084102.CrossRefGoogle ScholarPubMed
Leung, T., Swaminathan, N. & Davidson, P. A. 2012 Geometry and interaction of structures in homogeneous isotropic turbulence. J. Fluid Mech. 710, 453–481.CrossRefGoogle Scholar
Li, Z., Zhang, H., Bailey, S. C. C., Hoagg, J. B. & Martin, A. 2017 A data-driven adaptive Reynolds-averaged Navier–Stokes k–𝜔 model for turbulent flow. J. Comput. Phys. 345, 111–131.CrossRefGoogle Scholar
Lions, J. L. 1971 Optimal Control of Systems Governed by Partial Differential Equations. Springer.CrossRefGoogle Scholar
Meldi, M. & Poux, A. 2017 A reduced order model based on Kalman filtering for sequential data assimilation of turbulent flows. J. Comput. Phys. 347, 207–234.CrossRefGoogle Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32.CrossRefGoogle Scholar
Mons, V., Chassaing, J.-C., Gomez, T. & Sagaut, P. 2014 Is isotropic turbulence decay governed by asymptotic behavior of large scales? An eddy-damped quasi-normal Markvian-based data assimilation study. Phys. Fluids 26, 115105.CrossRefGoogle Scholar
Mons, V., Chassaing, J.-C., Gomez, T. & Sagaut, P. 2016 Reconstruction of unsteady viscous flows using data assimilation schemes. J. Comput. Phys. 316, 255–280.CrossRefGoogle Scholar
Mons, V., Chassaing, J.-C. & Sagaut, P. 2017 Optimal sensor placement for variational data assimilation of unsteady flows past a rotationally oscillating cylinder. J. Fluid Mech. 823, 230–277.CrossRefGoogle Scholar
Moshtagh, N.2009 Minimum volume enclosing ellipsoid. MATLAB Central File Exchange. Retrieved June 10, 2018.Google Scholar
Nocedal, J. & Wright, S. J. 1999 Numerical Optimization. Springer.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1992 Numerical Recipe in Fortran 77: The Art of Scientific Computing. Cambridge Universtiy Press.Google Scholar
Protas, B., Noack, B. R. & Osth, J. 2015 Optimal nonlinear eddy viscosity in Galerkin models of turbulent flows. J. Fluid Mech. 766, 337–367.CrossRefGoogle Scholar
Sagaut, P. 2002 Large Eddy Simulation for Incompressible Flows: An Introduction, 2nd edn. Springer.CrossRefGoogle Scholar
Schubert, E., Sander, J., Ester, M., Kriegel, H. P. & Xu, X. 2017 Dbscan revisited: why and how you should (still) use dbscan. ACM Trans. Database Syst. 42 (3), 19:1–19:21.CrossRefGoogle Scholar
Tao, B., Katz, J. & Meneveau, C. 2002 Statisticl geometry of subgrid-scale stresses determined from holographic particle image velocimetry measurements. J. Fluid Mech. 457, 35–78.CrossRefGoogle Scholar
Todds, M. J. 2016 Minimum-Volume Ellipsoids: Theory and Algorithms. SIAM.CrossRefGoogle Scholar
Vieillefosse, P. 1984 Internal motion of a small element of fluid in an inviscid flow. Physica A 125, 150–162.CrossRefGoogle Scholar
Wang, Q., Moin, P. & Iaccarino, G. 2009 Minimal repetition dynamic checkpointing algorithm for unsteady adjoint calculation. SIAM J. Sci. Comput. 31, 2549–2567.CrossRefGoogle Scholar
Yang, Y. & Pullin, D. I. 2011 Geometric study of Eulerian and Lagrangian structures in turbulent channel flows. J. Fluid Mech. 674, 67–92.CrossRefGoogle Scholar
Yoshida, K., Yamaguchi, J. & Kaneda, Y. 2005 Regeneration of small eddies by data assimilation in turbulence. Phys. Rev. Lett. 94, 014501.CrossRefGoogle ScholarPubMed