Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-30T20:26:31.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Solitary waves perturbed by a broad sill. Part 2. Propagation along the sill

Published online by Cambridge University Press:  26 November 2019

Harry Yeh Open the ORCID record for Harry Yeh [Opens in a new window] ,
Harrison Ko ,
Jeffrey Knowles Open the ORCID record for Jeffrey Knowles [Opens in a new window]  and
Samuel Harry
Harry Yeh*
Affiliation:
Department of Civil and Construction Engineering, Oregon State University, Corvallis, OR97331, USA
Harrison Ko
Affiliation:
Department of Civil and Construction Engineering, Oregon State University, Corvallis, OR97331, USA
Jeffrey Knowles
Affiliation:
Department of Civil and Construction Engineering, Oregon State University, Corvallis, OR97331, USA
Samuel Harry
Affiliation:
Department of Civil and Construction Engineering, Oregon State University, Corvallis, OR97331, USA
*
†Email address for correspondence: harry@oregonstate.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

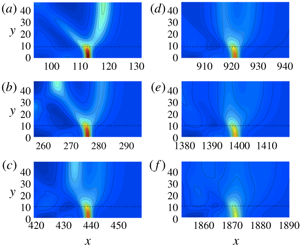
Evolution of a solitary wave travelling along a submerged sill is studied. The disturbance from the sill creates a phase lag along the wave crest between the ambient water depth and the shallower depth over the sill. This phase lag causes wave diffraction between the different parts of the wave, which induces radiating waves off the edge of the sill. The radiating waves act as an outlet for wave energy, resulting in significant and continual amplitude reduction of the solitary wave. Findings from laboratory experiments are confirmed numerically by simulating a much longer propagation distance with different sill breadths. When the sill breadth is narrow, the solitary wave slowly attenuates by wave radiation, maintaining a quasi-steady wave pattern. This is not the case for a broader sill. The resulting phase lag on the sill continually changes the wave pattern and the attenuation rate is substantially greater than the rate for the case of the narrow sill. The significant energy radiation together with the continual change in the wave formation eventually leads to the complete annihilation of the solitary wave in a wave tank. We also report a wave-breaking process along the sill observed in laboratory experiments. This breaking is induced when the wave amplitude on the sill is smaller than the maximum amplitude of a solitary wave in a uniform depth. Also found is the wake-like formation of gravity–capillary waves behind the breaking crest forming on the sill. Other features associated with the breaking are presented.

JFM classification

Waves/Free-surface Flows: Solitary waves Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave scattering
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A26
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benjamin, T. B. 1972 The stability of solitary waves. Proc. R. Soc. Lond. A 328 (1573), 153–183.CrossRefGoogle Scholar
Boyce, W. E., Diprima, R. C. & Meade, D. B. 1992 Elementary Differential Equations and Boundary Value Problems, vol. 9. Wiley.Google Scholar
Chen, Y. & Yeh, H. 2014 Laboratory experiments on counter-propagating collisions of solitary waves. Part 1. Wave interactions. J. Fluid Mech. 749, 577–596.CrossRefGoogle Scholar
Chen, Y., Zhang, E. & Yeh, H. 2014 Laboratory experiments on counter-propagating collisions of solitary waves. Part 2. Flow field. J. Fluid Mech. 755, 463–484.CrossRefGoogle Scholar
Craig, W. & Sulem, C. 1993 Numerical simulation of gravity waves. J. Comput. Phys. 108 (1), 73–83.CrossRefGoogle Scholar
Dommermuth, D. G. & Yue, D. K. 1987 A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mech. 184, 267–288.CrossRefGoogle Scholar
Duncan, J. H. 2001 Spilling breakers. Annu. Rev. Fluid Mech. 33 (1), 519–547.CrossRefGoogle Scholar
Gouin, M., Ducrozet, G. & Ferrant, P. 2016 Development and validation of a non-linear spectral model for water waves over variable depth. Eur. J. Mech. (B/Fluids) 57, 115–128.CrossRefGoogle Scholar
Grimshaw, R. 1971 The solitary wave in water of variable depth. Part 2. J. Fluid Mech. 46 (3), 611–622.CrossRefGoogle Scholar
Guyenne, P. & Nicholls, D. P. 2005 Numerical simulation of solitary waves on plane slopes. Maths Comput. Simulation 69 (3–4), 269–281.CrossRefGoogle Scholar
Jia, Y.2014 Numerical study of the kp solitons and higher order miles theory of the mach reflection in shallow water. PhD thesis, The Ohio State University.Google Scholar
Kadomtsev, B. B. & Petviashvili, V. I. 1970 On the stability of solitary waves in weakly dispersive media. Sov. Phys. Dokl. 15, 539–541.Google Scholar
Keulegan, G. H. 1948 Gradual damping of solitary waves. J. Res. Natl Bur. Stand 40 (6), 487–498.CrossRefGoogle Scholar
Knowles, J. & Yeh, H. 2018 On shoaling of solitary waves. J. Fluid Mech. 848, 1073–1097.CrossRefGoogle Scholar
Knowles, J. & Yeh, H. 2019 Fourfold amplification of solitary-wave mach reflection at a vertical wall. J. Fluid Mech. 861, 517–523.CrossRefGoogle Scholar
Ko, H. & Yeh, H. 2019 Solitary waves perturbed by a broad sill. Part 1. Propagation across the sill. J. Fluid Mech. 880, 916–934.CrossRefGoogle Scholar
Kodama, Y. 2018 Solitons in Two-Dimensional Shallow Water, vol. 92. SIAM.CrossRefGoogle Scholar
Li, W., Yeh, H. & Kodama, Y. 2011 On the mach reflection of a solitary wave: revisited. J. Fluid Mech. 672, 326–357.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Fenton, J. D. 1974 On the mass, momentum, energy and circulation of a solitary wave. ii. Proc. R. Soc. Lond. A 340 (1623), 471–493.CrossRefGoogle Scholar
Miles, J. W. 1980 Solitary waves. Annu. Rev. Fluid Mech. 12, 11–43.CrossRefGoogle Scholar
Russell, J. S. 1885 The Wave of Translation in the Oceans of Water, Air, and Ether. Trübner & Co.Google Scholar
Tanaka, M. 1993 Mach reflection of a large-amplitude solitary wave. J. Fluid Mech. 248, 637–661.CrossRefGoogle Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9 (2), 190–194.CrossRefGoogle Scholar