Article contents
Some insights for the prediction of near-wall turbulence
Published online by Cambridge University Press: 16 April 2013
Abstract
In this paper, we revisit the eddy viscosity formulation to highlight a number of important issues that have direct implications for the prediction of near-wall turbulence. For steady wall-bounded turbulent flows, we make the equilibrium assumption between rates of production ( 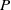 $P$ ) and dissipation (
$P$ ) and dissipation (  $\epsilon $ ) of turbulent kinetic energy (
$\epsilon $ ) of turbulent kinetic energy ( 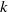 $k$ ) in the near-wall region to propose that the eddy viscosity should be given by
$k$ ) in the near-wall region to propose that the eddy viscosity should be given by 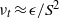 ${\nu }_{t} \approx \epsilon / {S}^{2} $ , where
${\nu }_{t} \approx \epsilon / {S}^{2} $ , where 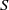 $S$ is the mean shear rate. We then argue that the appropriate velocity scale is given by
$S$ is the mean shear rate. We then argue that the appropriate velocity scale is given by 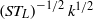 $\mathop{(S{T}_{L} )}\nolimits ^{- 1/ 2} {k}^{1/ 2} $ where
$\mathop{(S{T}_{L} )}\nolimits ^{- 1/ 2} {k}^{1/ 2} $ where 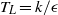 ${T}_{L} = k/ \epsilon $ is the turbulence (decay) time scale. The difference between this velocity scale and the commonly assumed velocity scale of
${T}_{L} = k/ \epsilon $ is the turbulence (decay) time scale. The difference between this velocity scale and the commonly assumed velocity scale of 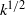 ${k}^{1/ 2} $ is subtle but the consequences are significant for near-wall effects. We then extend our discussion to show that the fundamental length and time scales that capture the near-wall behaviour in wall-bounded shear flows are the shear mixing length scale
${k}^{1/ 2} $ is subtle but the consequences are significant for near-wall effects. We then extend our discussion to show that the fundamental length and time scales that capture the near-wall behaviour in wall-bounded shear flows are the shear mixing length scale 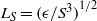 ${L}_{S} = \mathop{(\epsilon / {S}^{3} )}\nolimits ^{1/ 2} $ and the mean shear time scale
${L}_{S} = \mathop{(\epsilon / {S}^{3} )}\nolimits ^{1/ 2} $ and the mean shear time scale 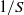 $1/ S$ , respectively. With these appropriate length and time scales (or equivalently velocity and time scales), the eddy viscosity can be rewritten in the familiar form of the
$1/ S$ , respectively. With these appropriate length and time scales (or equivalently velocity and time scales), the eddy viscosity can be rewritten in the familiar form of the 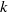 $k$ –
$k$ –  $\epsilon $ model as
$\epsilon $ model as 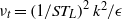 ${\nu }_{t} = \mathop{(1/ S{T}_{L} )}\nolimits ^{2} {k}^{2} / \epsilon $ . We use the direct numerical simulation (DNS) data of turbulent channel flow of Hoyas & Jiménez (Phys. Fluids, vol. 18, 2006, 011702) and the turbulent boundary layer flow of Jiménez et al. (J. Fluid Mech. vol. 657, 2010, pp. 335–360) to perform ‘a priori’ tests to check the validity of the revised eddy viscosity formulation. The comparisons with the exact computations from the DNS data are remarkable and highlight how well the equilibrium assumption holds in the near-wall region. These findings could prove to be useful in near-wall modelling of turbulent flows.
${\nu }_{t} = \mathop{(1/ S{T}_{L} )}\nolimits ^{2} {k}^{2} / \epsilon $ . We use the direct numerical simulation (DNS) data of turbulent channel flow of Hoyas & Jiménez (Phys. Fluids, vol. 18, 2006, 011702) and the turbulent boundary layer flow of Jiménez et al. (J. Fluid Mech. vol. 657, 2010, pp. 335–360) to perform ‘a priori’ tests to check the validity of the revised eddy viscosity formulation. The comparisons with the exact computations from the DNS data are remarkable and highlight how well the equilibrium assumption holds in the near-wall region. These findings could prove to be useful in near-wall modelling of turbulent flows.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 12
- Cited by

