Article contents
Spatial structure of shock formation
Published online by Cambridge University Press: 05 May 2017
Abstract
The formation of a singularity in a compressible gas, as described by the Euler equation, is characterized by the steepening and eventual overturning of a wave. Using self-similar variables in two space dimensions and a power series expansion based on powers of 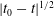 $|t_{0}-t|^{1/2}$ ,
$|t_{0}-t|^{1/2}$ , 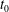 $t_{0}$ being the singularity time, we show that the spatial structure of this process, which starts at a point, is equivalent to the formation of a caustic, i.e. to a cusp catastrophe. The lines along which the profile has infinite slope correspond to the caustic lines, from which we construct the position of the shock. By solving the similarity equation, we obtain a complete local description of wave steepening and of the spreading of the shock from a point. The shock spreads in the transversal direction as
$t_{0}$ being the singularity time, we show that the spatial structure of this process, which starts at a point, is equivalent to the formation of a caustic, i.e. to a cusp catastrophe. The lines along which the profile has infinite slope correspond to the caustic lines, from which we construct the position of the shock. By solving the similarity equation, we obtain a complete local description of wave steepening and of the spreading of the shock from a point. The shock spreads in the transversal direction as 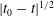 $|t_{0}-t|^{1/2}$ and in the direction of propagation as
$|t_{0}-t|^{1/2}$ and in the direction of propagation as 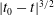 $|t_{0}-t|^{3/2}$ , as also found in a one-dimensional model problem.
$|t_{0}-t|^{3/2}$ , as also found in a one-dimensional model problem.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 9
- Cited by


