Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T16:02:06.702Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral content of cloud cavitation about a sphere

Published online by Cambridge University Press:  22 December 2016

K. L. de Graaf Open the ORCID record for K. L. de Graaf [Opens in a new window] ,
P. A. Brandner Open the ORCID record for P. A. Brandner [Opens in a new window]  and
B. W. Pearce Open the ORCID record for B. W. Pearce [Opens in a new window]
K. L. de Graaf*
Affiliation:
Australian Maritime College, University of Tasmania, Launceston, TAS 7250, Australia
P. A. Brandner
Affiliation:
Australian Maritime College, University of Tasmania, Launceston, TAS 7250, Australia
B. W. Pearce
Affiliation:
Australian Maritime College, University of Tasmania, Launceston, TAS 7250, Australia
*
†Email address for correspondence: kdegraaf@amc.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

The physics and spectral content of cloud cavitation about a sphere are investigated in a variable-pressure water tunnel using dynamic surface pressure measurement and high-speed imaging. Experiments are conducted using a polyvinyl chloride sphere at a Reynolds number of 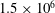$1.5\times 10^{6}$ with cavitation numbers, $\unicode[STIX]{x1D70E}$, ranging from inception to supercavitation. Three distinct shedding regimes are identified: a uni-modal regime for 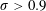$\unicode[STIX]{x1D70E}>0.9$ and two bi-modal regimes for 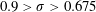$0.9>\unicode[STIX]{x1D70E}>0.675$ and 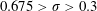$0.675>\unicode[STIX]{x1D70E}>0.3$. For small cavity lengths (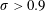$\unicode[STIX]{x1D70E}>0.9$), Kelvin–Helmholtz instability and transition to turbulence in the overlying separated boundary layer form the basis for cavity breakup and coherent vortex formation. At greater lengths (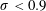$\unicode[STIX]{x1D70E}<0.9$), larger-scale shedding ensues, driven by coupled re-entrant jet formation and shockwave propagation. Strong adverse pressure gradients about the sphere lead to accumulation and radial growth of re-entrant flow, initiating breakup, from which, in every case, a condensation shockwave propagates upstream causing cavity collapse. When the shedding is most energetic, shockwave propagation upstream may cause large-scale leading edge extinction. The bi-modal response is due to cavity shedding being either axisymmetric or asymmetric. The two bi-modal regimes correspond to $\unicode[STIX]{x1D70E}$ ranges where the cavity and re-entrant jet either remain attached or become detached from the sphere. There is a distinct frequency offset at transition between regimes in both shedding modes. Despite the greater cavity lengths at lower $\unicode[STIX]{x1D70E}$ values, the second bi-modal regime initially exhibits shorter shedding periods due to increased cavity growth rates. The second regime persists until supercavitation develops for 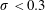$\unicode[STIX]{x1D70E}<0.3$.

JFM classification

Drops and Bubbles: Cavitation Multiphase and Particle-laden Flows: Multiphase flow Compressible Flows: Shock waves
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achenbach, E. 1972 Experiments on the flow past spheres at very high Reynolds numbers. J. Fluid Mech. 54 (3), 565–575.Google Scholar
Brandner, P. A., Walker, G. J., Niekamp, P. N. & Anderson, B. 2010 An experimental investigation of cloud cavitation about a sphere. J. Fluid Mech. 656, 147–176.CrossRefGoogle Scholar
Brennen, C. E. 2005 Fundamentals of Multiphase Flow. Cambridge University Press.Google Scholar
Callenaere, M., Franc, J.-P., Michel, J.-M. & Riondet, M. 2001 The cavitation instability induced by the development of a re-entrant jet. J. Fluid Mech. 444, 223–256.CrossRefGoogle Scholar
Coutier-Delgosha, O., Stutz, B., Vabre, A. & Legoupil, S. 2007 Analysis of cavitating flow structure by experimental and numerical investigations. J. Fluid Mech. 578, 171–222.Google Scholar
Ganesh, H., Mäkiharju, S. A. & Ceccio, S. L. 2016a Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities. J. Fluid Mech. 802, 37–78.Google Scholar
Ganesh, H., Wu, J. & Ceccio, S. L. 2016b Investigation of cavity shedding dynamics on a NACA0015 hydrofoil using time resolved x-ray densitometry. In 31st Symposium on Naval Hydrodynamics, ONR.Google Scholar
Gnanaskandan, A. & Mahesh, K. 2016a Large eddy simulation of the transition from sheet to cloud cavitation over a wedge. Intl J. Multiphase Flow 83, 86–102.Google Scholar
Gnanaskandan, A. & Mahesh, K. 2016b Numerical investigation of near-wake characteristics of cavitating flow over a circular cylinder. J. Fluid Mech. 790, 453–491.Google Scholar
de Graaf, K. L., Brandner, P. A. & Pearce, B. W. 2014 Spectral content of cloud cavitation about a sphere. In 19th Australasian Fluid Mechanics Conference, Paper 277. AFMS.Google Scholar
Guennoun, M. F.2006, Etude physique de l’apparition et du développement de la cavitation sur une aube isolée. PhD thesis, Laboratory for Hydraulic Machines, EPFL.Google Scholar
Kawakami, D. T., Qin, Q. & Arndt, R. 2005 Water quality and the periodicity of sheet/cloud cavitation. In ASME Cavitation and Multiphase Flow Forum.Google Scholar
Khlifa, I., Coutier-Delgosha, O., Fuzier, S. & Roussette, O. 2016 Investigation of the dynamics of cloud cavitation using fast x-ray imaging. In Sixteenth International Symposium on Transport Phenomena and Dynamics of Rotating Machinery (ISROMAC16). Honolulu, Hawaii, USA.Google Scholar
Pham, T. M., Michel, J. M. & Lecoffre, Y. 1997 Dynamical nuclei measurement: on the development and the performance evaluation of an optimized center-body meter. J. Fluids Engng 119 (4), 744–751.Google Scholar
Reisman, G. E., Wang, Y.-C. & Brennen, C. E. 1998 Observations of shock waves in cloud cavitation. J. Fluid Mech. 355, 255–283.Google Scholar
Stutz, B. & Reboud, J.-L. 1997 Two-phase flow structure of sheet cavitation. Phys. Fluids 9 (12), 3678–3686.Google Scholar
Stutz, B. & Reboud, J.-L. 2000 Measurements within unsteady cavitation. Exp. Fluids 29 (6), 545–552.Google Scholar
Torrence, C. & Compo, G. P. 1998 A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79 (1), 61–78.Google Scholar
Welch, P. D. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15 (2), 70–73.Google Scholar

de Graaf supplementary movie

σ = 1.0: Inception occurs at about σ = 1.0 where intermittent cavitation occurs around the circumference of minimum pressure.

Download de Graaf supplementary movie(Video)
Video 445.4 KB

de Graaf supplementary movie

σ = 0.9: The cavity is fully established with the leading edge composed of periodic laminar cells. The overlying laminar flow in the separating boundary layer transitions to turbulence with the formation of transverse waves due to Kelvin-Helmholtz (KH) instability. Cavity breakup at high σ values, where cavity lengths are small, is due to the development of these transverse waves that with intermittent roll-up are shed as coherent axisymmetric vortices

Download de Graaf supplementary movie(Video)
Video 887.4 KB

de Graaf supplementary movie

σ = 0.8: For 0.9 > σ > 0.8 shedding is uni-modal – cavity lengths are small and clouds are shed close to axisymmetrically.

Download de Graaf supplementary movie(Video)
Video 1.2 MB

de Graaf supplementary movie

σ = 0.7: For σ < 0.8 the interaction of the re-entrant flows on either side of the sphere create instability and asymmetric shedding. The cavity and re-entrant jet remain attached to the sphere.

Download de Graaf supplementary movie(Video)
Video 1.4 MB

de Graaf supplementary movie

σ = 0.6: For σ less than about 0.675 the cavity becomes detached from the sphere and the re-entrant jet can be seen to impinge downstream of the sphere. Instability and asymmetry in the shedding leads to frequent occurrences of converging re-entrant flows, creating local jetting. Shockwaves can be seen to propagate both upstream and circumferentially causing leading edge extinction over large regions of the circumference.

Download de Graaf supplementary movie(Video)
Video 1.6 MB

de Graaf supplementary movie

σ = 0.6: Cavitation occurrence is similar to σ = 0.6 except cavity lengths have increased, shedding frequencies have decreased and the frequency and duration of leading edge extinction events has reduced.

Download de Graaf supplementary movie(Video)
Video 1.7 MB

de Graaf supplementary movie

σ = 0.4: Cavity lengths are large and shedding events become less frequent. Shockwaves and cavity shedding events still occur but do not result in large scale extinction of the leading edge and/or the leading edge is re-nucleated so quickly such that few extinction events are observed.

Download de Graaf supplementary movie(Video)
Video 1.8 MB

de Graaf supplementary movie

σ = 0.75: A typical shedding cycle corresponding to the sequence of images shown in figure 4.

Download de Graaf supplementary movie(Video)
Video 308.4 KB