Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T20:04:28.411Z Has data issue: false hasContentIssue false
  • English
  • Français

Square cylinder in the interface of two different velocity streams

Published online by Cambridge University Press:  24 October 2022

R. El Mansy Open the ORCID record for R. El Mansy [Opens in a new window] ,
W. Sarwar Open the ORCID record for W. Sarwar [Opens in a new window] ,
J.M. Bergadà Open the ORCID record for J.M. Bergadà [Opens in a new window]  and
F. Mellibovsky Open the ORCID record for F. Mellibovsky [Opens in a new window]
R. El Mansy
Affiliation:
Fluid Mechanics Department, Universitat Politècnica de Catalunya, 08034 Barcelona, Spain
W. Sarwar
Affiliation:
Department of Physics, Aerospace Engineering Division, Universitat Politècnica de Catalunya, 08034 Barcelona, Spain
J.M. Bergadà
Affiliation:
Fluid Mechanics Department, Universitat Politècnica de Catalunya, 08034 Barcelona, Spain
F. Mellibovsky*
Affiliation:
Department of Physics, Aerospace Engineering Division, Universitat Politècnica de Catalunya, 08034 Barcelona, Spain
*
†Email address for correspondence: fernando.mellibovsky@upc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

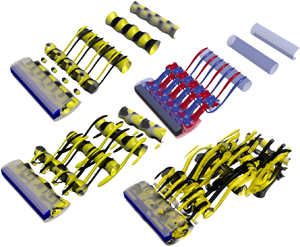
We investigate the incompressible flow past a square cylinder immersed in the wake of an upstream nearby splitter plate separating two streams of different velocity. The bottom stream Reynolds number, based on the square side, $Re_B=56$ is kept constant while the top-to-bottom Reynolds numbers ratio $R\equiv Re_T/Re_B$ is increased in the range $R\in [1,6.5]$, corresponding to a coupled variation of the bulk Reynolds number $Re\equiv (Re_T+Re_B)/2\in [56,210]$ and an equivalent non-dimensional shear parameter $K\equiv 2(R-1)/(R+1)\in [0,1.4667]$. The onset of vortex shedding is pushed to higher $Re$ as compared with the square cylinder in the classic configuration. The advent of three dimensionality is triggered by a mode-C-type instability, much as reported for open circular rings and square cylinders placed at an incidence. The domain of minimal spanwise-periodic extension that is capable of sustaining spatiotemporally chaotic dynamics, namely one accommodating about twice the wavelength of the dominant eigenmode, has been chosen for the analysis of the wake transition regime. The path towards spatiotemporal chaos is, in this minimal domain, initiated with a modulational period-doubling tertiary bifurcation that also doubles the spanwise periodicity. At slightly higher values of $R$, the flow has become spatiotemporally chaotic, but the main features of mode C are still clearly distinguishable. Although some of the nonlinear solutions found along the wake transition regime employing the minimal domain might indeed be unstable to long wavelength disturbances, they still are solutions of the infinite cylinder problem and are apt to play a relevant role in the inception of spatiotemporally chaotic dynamics.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Wakes/Jets: Vortex streets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 950 , 10 November 2022 , A30
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abdessemed, N., Sharma, A.S., Sherwin, S.J. & Theofilis, V. 2009 Transient growth analysis of the flow past a circular cylinder. Phys. Fluids 21 (4), 044103.CrossRefGoogle Scholar
Ahmed, F. & Rajaratnam, N. 1998 Flow around bridge piers. J.Hydraul. Engng ASCE 124 (3), 288–300.CrossRefGoogle Scholar
An, B., Bergada, J.M. & Mellibovsky, F. 2019 The lid-driven right-angled isosceles triangular cavity flow. J.Fluid Mech. 875, 476–519.CrossRefGoogle Scholar
An, B., Bergadà, J.M., Mellibovsky, F., Sang, W.M. & Xi, C. 2020 Numerical investigation on the flow around a square cylinder with an upstream splitter plate at low Reynolds numbers. Meccanica 55, 1037–1059.CrossRefGoogle Scholar
Ayukawa, K., Ochi, J., Kawahara, G. & Hirao, T. 1993 Effects of shear rate on the flow around a square cylinder in a uniform shear flow. J.Wind Engng Ind. Aerodyn. 50, 97–106.CrossRefGoogle Scholar
Bai, H. & Alam, M.M. 2018 Dependence of square cylinder wake on Reynolds number. Phys. Fluids 30 (1), 015102.CrossRefGoogle Scholar
Bailey, P.A. & Kwok, K.C.S. 1985 Interference excitation of twin tall buildings. J.Wind Engng Ind. Aerodyn. 21 (3), 323–338.CrossRefGoogle Scholar
Barkley, D. & Henderson, R.D. 1996 Three-dimensional floquet stability analysis of the wake of a circular cylinder. J.Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bhatt, R. & Alam, M.M. 2018 Vibrations of a square cylinder submerged in a wake. J.Fluid Mech. 853, 301–332.CrossRefGoogle Scholar
Blackburn, H.M. & Lopez, J.M. 2003 On three-dimensional quasiperiodic floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15 (8), L57–L60.CrossRefGoogle Scholar
Blackburn, H.M., Marques, F. & Lopez, J.M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J.Fluid Mech. 522, 395–411.CrossRefGoogle Scholar
Blackburn, H.M. & Sheard, G.J. 2010 On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 22 (3), 031701.CrossRefGoogle Scholar
Cantwell, C.D., et al. 2015 Nektar++: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.CrossRefGoogle Scholar
Cao, S., Ozono, S., Tamura, Y., Ge, Y. & Kikugawa, H. 2010 Numerical simulation of Reynolds number effects on velocity shear flow around a circular cylinder. J.Fluids Struct. 26 (5), 685–702.CrossRefGoogle Scholar
Cao, S., Zhou, Q. & Zhou, Z. 2014 Velocity shear flow over rectangular cylinders with different side ratios. Comput. Fluids 96, 35–46.CrossRefGoogle Scholar
Cheng, M., Whyte, D.S. & Lou, J. 2007 Numerical simulation of flow around a square cylinder in uniform-shear flow. J.Fluids Struct. 23 (2), 207–226.CrossRefGoogle Scholar
Choi, C.B., Jang, Y.J. & Yang, K.S. 2012 Secondary instability in the near-wake past two tandem square cylinders. Phys. Fluids 24 (2), 024102.CrossRefGoogle Scholar
Chomaz, J.M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Davis, R.W. & Moore, E.F. 1982 A numerical study of vortex shedding from rectangles. J.Fluid Mech. 116, 475–506.CrossRefGoogle Scholar
Durao, D.F.G., Heitor, M.V. & Pereira, J.C.F. 1988 Measurements of turbulent and periodic flows around a square cross-section cylinder. Exp. Fluids 6 (5), 298–304.CrossRefGoogle Scholar
El Mansy, R., Bergadà, J.M., Sarwar, W. & Mellibovsky, F. 2022 Aerodynamic performances and wake topology past a square cylinder in the interface of two different-velocity streams. Phys. Fluids 34 (6), 064106.CrossRefGoogle Scholar
Franke, R., Rodi, W. & Schönung, B. 1990 Numerical calculation of laminar vortex-shedding flow past cylinders. J.Wind Engng Ind. Aerodyn. 35, 237–257.CrossRefGoogle Scholar
Henderson, R.D. & Barkley, D. 1996 Secondary instability in the wake of a circular cylinder. Phys. Fluids 8 (6), 1683–1685.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P.A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Hunt, J.C.R., Wray, A.A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the Summer Program 1988, Center for Turbulence Research, N89-24555.Google Scholar
Hwang, R.R. & Sue, Y.C. 1997 Numerical simulation of shear effect on vortex shedding behind a square cylinder. Intl J. Numer. Meth. Fluids 25 (12), 1409–1420.3.0.CO;2-N>CrossRefGoogle Scholar
Hwang, R.R. & Yao, C.-C. 1997 A numerical study of vortex shedding from a square cylinder with ground effect. Trans. ASME J. Fluids Engng 119 (3), 512–518.CrossRefGoogle Scholar
Jimenez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J.Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Jordan, S.K. & Fromm, J.E. 1972 Laminar flow past a circle in a shear flow. Phys. Fluids 15 (6), 972–976.CrossRefGoogle Scholar
Kang, S., Choi, H. & Lee, S. 1999 Laminar flow past a rotating circular cylinder. Phys. Fluids 11 (11), 3312–3321.CrossRefGoogle Scholar
von Kármán, T. 1911 Über den mechanismus des wiederstandes, den ein bewegter korper in einer flüssigkeit erfährt. Nachr. Ges. Wiss. Göttingen 1911, 509–517.Google Scholar
von Kármán, T. 1912 Über den mechanismus des wiederstandes, den ein bewegter korper in einer flüssigkeit erfährt. Nachr. Ges. Wiss. Göttingen 1912, 547–556.Google Scholar
Kelkar, K.M. & Patankar, S.V. 1992 Numerical prediction of vortex shedding behind a square cylinder. Intl J. Numer. Meth. Fluids 14 (3), 327–341.CrossRefGoogle Scholar
Kiya, M., Tamura, H. & Arie, M. 1980 Vortex shedding from a circular cylinder in moderate-Reynolds-number shear flow. J.Fluid Mech. 101 (4), 721–735.CrossRefGoogle Scholar
Kumar, A. & Ray, R.K. 2015 Numerical study of shear flow past a square cylinder at Reynolds numbers 100, 200. Procedia Engng 127, 102–109.CrossRefGoogle Scholar
Kwon, T.S., Sung, H.J. & Hyun, J.M. 1992 Experimental investigation of uniform-shear flow past a circular cylinder. Trans. ASME J. Fluids Engng 114, 457–460.CrossRefGoogle Scholar
Lankadasu, A. & Vengadesan, S. 2008 Onset of vortex shedding in planar shear flow past a square cylinder. Intl J. Heat Fluid Flow 29 (4), 1054–1059.CrossRefGoogle Scholar
Lankadasu, A. & Vengadesan, S. 2009 Influence of inlet shear on the 3-D flow past a square cylinder at moderate Reynolds number. J.Fluids Struct. 25 (5), 889–896.CrossRefGoogle Scholar
Lankadasu, A. & Vengadesan, S. 2011 Shear effect on square cylinder wake transition characteristics. Intl J. Numer. Meth. Fluids 67 (9), 1115–1134.CrossRefGoogle Scholar
Lei, C., Cheng, L. & Kavanagh, K. 2000 A finite difference solution of the shear flow over a circular cylinder. Ocean Engng 27 (3), 271–290.CrossRefGoogle Scholar
Leweke, T. & Provansal, M. 1994 Model for the transition in bluff body wakes. Phys. Rev. Lett. 72 (20), 3174–3177.CrossRefGoogle ScholarPubMed
Leweke, T. & Provansal, M. 1995 The flow behind rings: bluff body wakes without end effects. J.Fluid Mech. 288, 265–310.CrossRefGoogle Scholar
Leweke, T., Provansal, M. & Boyer, L. 1993 Stability of vortex shedding modes in the wake of a ring at low Reynolds numbers. Phys. Rev. Lett. 71 (21), 3469–3472.CrossRefGoogle ScholarPubMed
Loucks, R.B. & Wallace, J.M. 2012 Velocity and velocity gradient based properties of a turbulent plane mixing layer. J.Fluid Mech. 699, 280–319.CrossRefGoogle Scholar
Luo, S.C., Chew, Y.T. & Ng, Y.T. 2003 Characteristics of square cylinder wake transition flows. Phys. Fluids 15 (9), 2549–2559.CrossRefGoogle Scholar
Luo, S.C., Tong, X.H. & Khoo, B.C. 2007 Transition phenomena in the wake of a square cylinder. J.Fluids Struct. 23 (2), 227–248.CrossRefGoogle Scholar
Lyn, D.A., Einav, S., Rodi, W. & Park, J.H. 1995 A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. J.Fluid Mech. 304, 285–319.CrossRefGoogle Scholar
Mahir, N. 2017 Three dimensional heat transfer from a square cylinder at low Reynolds numbers. Intl J. Therm. Sci. 119, 37–50.CrossRefGoogle Scholar
Mansy, H., Yang, P.M. & Williams, D.R. 1994 Quantitative measurements of three-dimensional structures in the wake of a circular cylinder. J.Fluid Mech. 270, 277–296.CrossRefGoogle Scholar
Marques, F., Lopez, J.M. & Blackburn, H.M. 2004 Bifurcations in systems with $\textrm {Z}_2$ spatio-temporal and O(2) spatial symmetry. Physica D 189 (3–4), 247–276.CrossRefGoogle Scholar
Mellibovsky, F. & Meseguer, A. 2015 A mechanism for streamwise localisation of nonlinear waves in shear flows. J.Fluid Mech. 779, R1.CrossRefGoogle Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J.Fluid Mech. 476, 303–334.CrossRefGoogle Scholar
Monkewitz, P.A. 1988 The absolute and convective nature of instability in two-dimensional wakes at low Reynolds-numbers. Phys. Fluids 31 (5), 999–1006.CrossRefGoogle Scholar
Monson, D.R. 1983 The effect of transverse curvature on the drag and vortex shedding of elongated bluff bodies at low Reynolds number. Trans. ASME J. Fluids Engng 105, 308–318.CrossRefGoogle Scholar
Moser, R.D. & Rogers, M.M. 1993 The three-dimensional evolution of a plane mixing layer: pairing and transition to turbulence. J.Fluid Mech. 247, 275–320.CrossRefGoogle Scholar
Moxey, D., et al. 2020 Nektar++: enhancing the capability and application of high-fidelity spectral/hp element methods. Comput. Phys. Commun. 249, 107110.CrossRefGoogle Scholar
Mushyam, A. & Bergada, J.M. 2017 A numerical investigation of wake and mixing layer interactions of flow past a square cylinder. Meccanica 52 (1), 107–123.CrossRefGoogle Scholar
Niu, X.-F., Li, Y. & Wang, X.-N. 2021 Numerical study of aerodynamic noise behaviors for a vertically-installed flat strut behind an asymmetrical airfoil. Eur. J. Mech. (B/Fluids) 88, 17–33.CrossRefGoogle Scholar
Noack, B.R. & Eckelmann, H. 1994 A global stability analysis of the steady and periodic cylinder wake. J.Fluid Mech. 270, 297–330.CrossRefGoogle Scholar
Norberg, C. 1993 Flow around rectangular cylinders: pressure forces and wake frequencies. J.Wind Engng Ind. Aerodyn. 49 (1–3), 187–196.CrossRefGoogle Scholar
Norberg, C. 1994 An experimental investigation of the flow around a circular cylinder: influence of aspect ratio. J.Fluid Mech. 258, 287–316.CrossRefGoogle Scholar
Norberg, C. 1996 Taken from Sohankar et al. Phys. Fluids 11 (2), 288–306 (1999).Google Scholar
Okajima, A. 1982 Strouhal numbers of rectangular cylinders. J.Fluid Mech. 123, 379–398.CrossRefGoogle Scholar
Park, D. & Yang, K.S. 2016 Flow instabilities in the wake of a rounded square cylinder. J.Fluid Mech. 793, 915–932.CrossRefGoogle Scholar
Park, D. & Yang, K.-S. 2018 Effects of planar shear on the three-dimensional instability in flow past a circular cylinder. Phys. Fluids 30 (3), 034103.CrossRefGoogle Scholar
Posdziech, O. & Grundmann, R. 2001 Numerical simulation of the flow around an infinitely long circular cylinder in the transition regime. Theor. Comput. Fluid Dyn. 15 (2), 121–141.Google Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard–von Kármán instability: transient and forced regimes. J.Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Ray, R.K. & Kumar, A. 2017 Numerical study of shear rate effect on unsteady flow separation from the surface of the square cylinder using structural bifurcation analysis. Phys. Fluids 29 (8), 083604.CrossRefGoogle Scholar
Robichaux, J., Balachandar, S. & Vanka, S.P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11 (3), 560–578.CrossRefGoogle Scholar
Rogers, M.M. & Moser, R.D. 1992 The three-dimensional evolution of a plane mixing layer: the Kelvin–Helmholtz rollup. J.Fluid Mech. 243, 183–226.CrossRefGoogle Scholar
Saha, A.K., Biswas, G. & Muralidhar, K. 1999 Influence of inlet shear on structure of wake behind a square cylinder. J.Engng Mech. ASCE 125 (3), 359–363.CrossRefGoogle Scholar
Saha, A.K., Biswas, G. & Muralidhar, K. 2003 Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Intl J. Heat Fluid Flow 24 (1), 54–66.CrossRefGoogle Scholar
Sheard, G.J. 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J.Fluids Struct. 27 (5–6), 734–742.CrossRefGoogle Scholar
Sheard, G.J., Fitzgerald, M.J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J.Fluid Mech. 630, 43–69.CrossRefGoogle Scholar
Sheard, G.J., Hourigan, K. & Thompson, M.C. 2005 a Computations of the drag coefficients for low-Reynolds-number flow past rings. J.Fluid Mech. 526, 257–275.CrossRefGoogle Scholar
Sheard, G.J., Thompson, M.C. & Hourigan, K. 2003 From spheres to circular cylinders: the stability and flow structures of bluff ring wakes. J.Fluid Mech. 492, 147–180.CrossRefGoogle Scholar
Sheard, G.J., Thompson, M.C. & Hourigan, K. 2005 b Subharmonic mechanism of the mode C instability. Phys. Fluids 17 (11), 111702.CrossRefGoogle Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1998 Low-Reynolds-number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition. Intl J. Numer. Meth. Fluids 26 (1), 39–56.3.0.CO;2-P>CrossRefGoogle Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1999 Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 11 (2), 288–306.CrossRefGoogle Scholar
Sohankar, A., Rangraz, E., Khodadadi, M. & Alam, M.M. 2020 Fluid flow and heat transfer around single and tandem square cylinders subjected to shear flow. J.Braz. Soc. Mech. Sci. Engng 42 (8), 1–22.Google Scholar
Sung, H.J., Chun, C.K. & Hyun, J.M. 1995 Experimental study of uniform-shear flow past a rotating cylinder. Trans. ASME J. Fluids Engng 117 (1), 62–67.CrossRefGoogle Scholar
Tamura, H., Kiya, M. & Arie, M. 1980 Numerical study on viscous shear flow past a circular cylinder. Bull. JSME 23 (186), 1952–1958.CrossRefGoogle Scholar
Tong, X.H., Luo, S.C. & Khoo, B.C. 2008 Transition phenomena in the wake of an inclined square cylinder. J.Fluids Struct. 24 (7), 994–1005.CrossRefGoogle Scholar
Williamson, C.H.K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31 (11), 3165–3168.CrossRefGoogle Scholar
Williamson, C.H.K. 1992 The natural and forced formation of spot-like vortex dislocations in the transition of a wake. J.Fluid Mech. 243, 393–441.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 a Mode A secondary instability in wake transition. Phys. Fluids 8 (6), 1680–1682.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 b Three-dimensional wake transition. J.Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 c Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Yang, X. & Zebib, A. 1989 Absolute and convective instability of a cylinder wake. Phys. Fluids A 1 (4), 689–696.CrossRefGoogle Scholar
Yoon, D.H., Yang, K.S. & Choi, C.B. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22 (4), 043603.CrossRefGoogle Scholar
Yoshino, F. & Hayashi, T. 1984 The numerical solution of flow around a rotating circular cylinder in uniform shear flow. Bull. JSME 27 (231), 1850–1857.CrossRefGoogle Scholar
Zhang, H.J., Huang, L. & Zhou, Y. 2005 Aerodynamic loading on a cylinder behind an airfoil. Exp. Fluids 38 (5), 588–593.CrossRefGoogle Scholar

El Mansy et al. supplementary movie 1

See pdf file for movie caption

Download El Mansy et al. supplementary movie 1(Video)
Video 27.9 MB

El Mansy et al. supplementary movie 2

See pdf file for movie caption

Download El Mansy et al. supplementary movie 2(Video)
Video 9.2 MB

El Mansy et al. supplementary movie 3

See pdf file for movie caption

Download El Mansy et al. supplementary movie 3(Video)
Video 38.9 MB

El Mansy et al. supplementary movie 4

See pdf file for movie caption

Download El Mansy et al. supplementary movie 4(Video)
Video 10.1 MB

El Mansy et al. supplementary movie 5

See pdf file for movie caption

Download El Mansy et al. supplementary movie 5(Video)
Video 12.5 MB

El Mansy et al. supplementary movie 6

See pdf file for movie caption

Download El Mansy et al. supplementary movie 6(Video)
Video 3.3 MB

El Mansy et al. supplementary movie 7

See pdf file for movie caption

Download El Mansy et al. supplementary movie 7(Video)
Video 2.8 MB

El Mansy et al. supplementary movie 8

See pdf file for movie caption

Download El Mansy et al. supplementary movie 8(Video)
Video 4 MB
Supplementary material: PDF

El Mansy et al. supplementary material

Captions for movies 1-8

Download El Mansy et al. supplementary material(PDF)
PDF 52.6 KB