Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-30T21:18:27.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and collapse of holes in liquid layers

Published online by Cambridge University Press:  24 September 2018

Cunjing Lv ,
Michael Eigenbrod  and
Steffen Hardt Open the ORCID record for Steffen Hardt [Opens in a new window]
Cunjing Lv
Affiliation:
Institute for Nano- and Microfluidics, Technische Universität Darmstadt, 64287 Darmstadt, Germany Department of Engineering Mechanics, Tsinghua University, 100084 Beijing, China
Michael Eigenbrod
Affiliation:
Institute for Nano- and Microfluidics, Technische Universität Darmstadt, 64287 Darmstadt, Germany
Steffen Hardt*
Affiliation:
Institute for Nano- and Microfluidics, Technische Universität Darmstadt, 64287 Darmstadt, Germany
*
†Email address for correspondence: hardt@nmf.tu-darmstadt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate experimentally and theoretically the stability and collapse of holes in liquid layers on bounded substrates with various wettabilities. It is shown that for a liquid layer with a thickness of the order of the capillary length, a stable hole exists when the hole diameter is bigger than a critical value 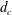$d_{c}$. Consequently, a further increase of the liquid volume causes the hole to collapse. It is found that 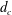$d_{c}$ increases with the size of the container, but its dependence on the contact angle is very weak. The experimental results are compared with theory, and good agreement is obtained. Moreover, we present investigations of the dynamics of the hole and the evolution of the liquid film profile after the collapse. The diameter of the hole during collapse and the minimum thickness of the liquid film shortly after the collapse obey different power laws with time. Simple theoretical models are developed which indicate that the collapse of the hole is triggered by surface tension and the subsequent closure process results from inertia, whereas the growth of the liquid column after hole closure results from the balance between the capillary force and inertia. Corresponding scaling coefficients are determined.

JFM classification

Interfacial Flows (free surface): Contact lines Instability: Instability Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 1130 - 1155
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bankoff, S. G., Johnson, M. F. G., Miksis, M. J., Schluter, R. A. & Lopez, P. G. 2003 Dynamics of a dry spot. J. Fluid Mech. 486, 239–259.Google Scholar
Bird, J. C., Ristenpart, W. D., Belmonte, A. & Stone, H. A. 2009 Critical angle for electrically driven coalescence of two conical droplets. Phys. Rev. Lett. 103 (16), 164502.Google Scholar
Bostwick, J. B., Dijksman, J. A. & Shearer, M. 2017 Wetting dynamics of a collapsing fluid hole. Phys. Rev. Fluids 2 (1), 014006.Google Scholar
Brakke, K. A. 1992 The surface evolver. Exp. Math. 1 (2), 141–165.Google Scholar
Burton, J. C., Waldrep, R. & Taborek, P. 2005 Scaling and instabilities in bubble pinch-off. Phys. Rev. Lett. 94 (18), 184502.Google Scholar
Cho, Y. S., Yi, Gi. R., Lim, J. M., Kim, S. H., Manoharan, V. N., Pine, D. J. & Yang, S. M. 2005 Self-organization of bidisperse colloids in water droplets. J. Am. Chem. Soc. 127 (45), 15968–15975.Google Scholar
Chou, T. H., Hong, S. J., Liang, Y. E., Tsao, H. K. & Sheng, Y. J. 2011 Equilibrium phase diagram of drop-on-fiber: coexistent states and gravity effect. Langmuir 27 (7), 3685–3692.Google Scholar
Courbin, L., Bird, J. C., Reyssat, M. & Stone, H. A. 2009 Dynamics of wetting: from inertial spreading to viscous imbibition. J. Phys.: Condens. Matter 21 (46), 464127.Google Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81 (3), 1131–1198.Google Scholar
Crawford, S., Lim, S. K. & Gradecak, S. 2013 Fundamental insights into nanowire diameter modulation and the liquid/solid interface. Nano Lett. 13 (1), 226–232.Google Scholar
Debrégeas, G., De Gennes, P.-G. & Brochard-Wyart, F. 1998 The life and death of ‘bare’ viscous bubbles. Science 279 (5357), 1704–1707.Google Scholar
Diez, J. A., Gratton, R. & Gratton, J. 1992 Selfsimilar solution of the second kind for a convergent viscous gravity current. Phys. Fluids A 4 (6), 1148–1155.Google Scholar
Dijksman, J. A., Mukhopadhyay, S., Gaebler, C., Witelski, T. P. & Behringer, R. P. 2015 Obtaining self-similar scalings in focusing flows. Phys. Rev. E 92 (4), 043016.Google Scholar
Duchemin, L., Eggers, J. & Josserand, C. 2003 Inviscid coalescence of drops. J. Fluid Mech. 487, 167–178.Google Scholar
Eddi, A., Winkels, K. G. & Snoeijer, J. H. 2013 Influence of droplet geometry on the coalescence of low viscosity drops. Phys. Rev. Lett. 111 (14), 144502.Google Scholar
Eggers, J., Fontelos, M. A., Leppinen, D. & Snoeijer, J. H. 2007 Theory of the collapsing axisymmetric cavity. Phys. Rev. Lett. 98 (9), 094502.Google Scholar
Eggers, J., Lister, J. R. & Stone, H. A. 1999 Coalescence of liquid drops. J. Fluid Mech. 401, 293–310.Google Scholar
Eifert, A., Paulssen, D., Varanakkottu, S. N., Baier, T. & Hardt, S. 2014 Simple fabrication of robust water-repellent surfaces with low contact-angle hysteresis based on impregnation. Adv. Mater. Interfaces 1 (3), 1300138.Google Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2003 Capillarity and Wetting Phenomena. Springer.Google Scholar
Gordillo, J. M., Sevilla, A., Rodríguez-Rodríguez, J. & Martinez-Bazan, C. 2005 Axisymmetric bubble pinch-off at high Reynolds numbers. Phys. Rev. Lett. 95 (19), 194501.Google Scholar
Kabla, A. & Debregeas, G. 2007 Quasi-static rheology of foams. Part 1. Oscillating strain. J. Fluid Mech. 587, 23–44.Google Scholar
Lamb, H. 1916 Statics. Cambridge University Press.Google Scholar
Langbein, D. W. 2002 Capillary Surfaces: Shape-Stability-Dynamics, in Particular Under Weightlessness, 178 edn. Springer Science & Business Media.Google Scholar
Leppinen, D. & Lister, J. R. 2005 Capillary pinch-off of inciscid fluids at varying density ratios: the bubble limit. Bull. Am. Phys. Soc. 50, 63 (abstract only).Google Scholar
Longuet-Higgins, M., Kerman, B. R. & Lunde, K. 1991 The release of air bubbles from an underwater nozzle. J. Fluid Mech. 230, 365–390.Google Scholar
López, P. G., Miksis, M. J. & Bankoff, S. G. 2001 Stability and evolution of a dry spot. Phys. Fluids 13 (6), 1601–1614.Google Scholar
Magnus, W., Oberhettinger, F. & Soni, R. P. 1966 Formulas and Theorems for the Special Functions of Mathematical Physics, 3rd edn. Springer.Google Scholar
de Maleprade, H., Clanet, C. & Quéré, D. 2016 Spreading of bubbles after contacting the lower side of an aerophilic slide immersed in water. Phys. Rev. Lett. 117 (9), 094501.Google Scholar
Moriarty, J. A. & Schwartz, L. W. 1993 Dynamic considerations in the closing and opening of holes in thin liquid films. J. Colloid Interface Sci. 161 (2), 335–342.Google Scholar
Norbury, J., Sander, G. C. & Scott, C. F. 2004 Corner solutions of the Laplace–Young equation. Q. J. Mech. Appl. Maths 60 (1), 1–16.Google Scholar
Oguz, H. N. & Prosperetti, A. 1993 Dynamics of bubble growth and detachment from a needle. J. Fluid Mech. 257, 111.Google Scholar
Padday, J. F. 1971 The profiles of axially symmetric menisci. Phil. Trans. R. Soc. Lond. A 269 (1197), 265–293.Google Scholar
Paulsen, J. D., Carmigniani, R., Kannan, A., Burton, J. C. & Nagel, S. R. 2014 Coalescence of bubbles and drops in an outer fluid. Nat. Commun. 5, 3182.Google Scholar
Redon, C., Brochard-Wyart, F. & Rondelez, F. 1991 Dynamics of dewetting. Phys. Rev. Lett. 66 (6), 715–718.Google Scholar
Ristenpart, W. D., McCalla, P. M., Roy, R. V. & Stone, H. A. 2006 Coalescence of spreading droplets on a wettable substrate. Phys. Rev. Lett. 97 (6), 064501.Google Scholar
Sharma, A. & Ruckenstein, E. 1990 Energetic criteria for the breakup of liquid films on nonwetting solid surfaces. J. Colloid Interface Sci. 137 (2), 433–445.Google Scholar
Song, J. L., Xu, W. J., Liu, X., Lu, Y. & Sun, J. 2012 Electrochemical machining of super-hydrophobic Al surfaces and effect of processing parameters on wettability. Appl. Phys. A 108 (3), 559–568.Google Scholar
Taylor, G. I. & Michael, D. H. 1973 On making holes in a sheet of fluid. J. Fluid Mech. 58 (04), 625–639.Google Scholar
Texier, B. D., Piroird, K., Quéré, D. & Clanet, C. 2013 Inertial collapse of liquid rings. J. Fluid Mech. 717, R3.Google Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2007 Experiments on bubble pinch-off. Phys. Fluids 19 (4), 042101.Google Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K. & Ootsuka, N. 2005 On the coalescence speed of bubbles. Phys. Fluids 17 (7), 07170.Google Scholar
Wilson, S. K. & Duffy, B. R. 1996 An asymptotic analysis of small holes in thin fluid layers. J. Engng Maths 30 (4), 445–457.Google Scholar
Zheng, Z., Fontelos, M. A., Shin, S., Dallaston, M. C., Tseluiko, D., Kalliadasis, S. & Stone, H. A. 2018a Healing capillary films. J. Fluid Mech. 838, 404–434.Google Scholar
Zheng, Z., Fontelos, M. A., Shin, S. & Stone, H. A. 2018b Universality in the nonlinear leveling of capillary films. Phys. Rev. Fluids 3 (3), 032001.Google Scholar

Lv et al. supplementary movie 1

Hole collapse on a superhydrophobic Al plate viewed from the top. Initially, the hole diameter decreases very slowly when adding more water. The dynamics speed up significantly when d reaches dc.

Download Lv et al. supplementary movie 1(Video)
Video 1.8 MB
Supplementary material: PDF

Lv et al. supplementary material

Supplementary material

Download Lv et al. supplementary material(PDF)
PDF 771.4 KB

Lv et al. supplementary movie 2

Same experiment as is movie 1, but captured from the side. This movie starts after instability has already set in. After hole collapse, an air bubble is formed on the surface but finally vanishes in the indentations.

Download Lv et al. supplementary movie 2(Video)
Video 812.6 KB

Lv et al. supplementary movie 3

Hole collapse in a water layer on a Teflon substrate in side view. After the hole is completely closed, there is an air bubble left at the center of the substrate.

Download Lv et al. supplementary movie 3(Video)
Video 608.7 KB

Lv et al. supplementary movie 4

Hole collapse on a hydrophilic silicon wafer in the side view. Different from the other three samples, here an acute angle at the three-phase contact line is observed. Line pinning is observed in the first stage when the hole is stable. However, beyond the stability threshold the hole collapses rather smoothly.

Download Lv et al. supplementary movie 4(Video)
Video 386.1 KB

Lv et al. supplementary movie 5

High-speed video of the final stages of hole collapse on a superhydrophobic Al substrate in side view (recording speed 100 000 fps).

Download Lv et al. supplementary movie 5(Video)
Video 561.9 KB