Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T17:23:30.965Z Has data issue: false hasContentIssue false
  • English
  • Français

The stability and nonlinear evolution of quasi-geostrophic toroidal vortices

Published online by Cambridge University Press:  22 January 2019

Jean N. Reinaud Open the ORCID record for Jean N. Reinaud [Opens in a new window]  and
David G. Dritschel Open the ORCID record for David G. Dritschel [Opens in a new window]
Jean N. Reinaud*
Affiliation:
Mathematical Institute, University of St Andrews, North Haugh, St Andrews KY16 9SS, UK
David G. Dritschel
Affiliation:
Mathematical Institute, University of St Andrews, North Haugh, St Andrews KY16 9SS, UK
*
†Email address for correspondence: jean.reinaud@st-andrews.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the linear stability and nonlinear evolution of a three-dimensional toroidal vortex of uniform potential vorticity under the quasi-geostrophic approximation. The torus can undergo a primary instability leading to the formation of a circular array of vortices, whose radius is approximately the same as the major radius of the torus. This occurs for azimuthal instability mode numbers 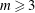$m\geqslant 3$, on sufficiently thin tori. The number of vortices corresponds to the azimuthal mode number of the most unstable mode growing on the torus. This value of 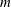$m$ depends on the ratio of the torus’ major radius to its minor radius, with thin tori favouring high mode 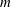$m$ values. The resulting array is stable when 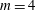$m=4$ and 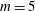$m=5$ and unstable when 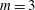$m=3$ and 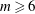$m\geqslant 6$. When 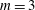$m=3$ the array has barely formed before it collapses towards its centre with the ejection of filamentary debris. When 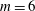$m=6$ the vortices exhibit oscillatory staggering, and when 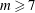$m\geqslant 7$ they exhibit irregular staggering followed by substantial vortex migration, e.g. of one vortex to the centre when 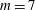$m=7$. We also investigate the effect of an additional vortex located at the centre of the torus. This vortex alters the stability properties of the torus as well as the stability properties of the circular vortex array formed from the primary toroidal instability. We show that a like-signed central vortex may stabilise a circular 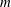$m$-vortex array with 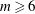$m\geqslant 6$.

JFM classification

Geophysical and Geological Flows: Quasi-geostrophic flows Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 60 - 78
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adriani, A., Mura, A., Orton, G., Hansen, C., Altieri, F., Moriconi, M. L., Rogers, J., Eichstdt, G., Momary, T., Ingersoll, A. P., Filacchione, G., Sindoni, G., Tabataba-Vakili, F., Dinelli, B. M., Fabiano, F., Bolton, S. J., Connerney, J. E. P., Atreya, S. K., Lunine, J. I., Tosi, F., Migliorini, A., Grassi, D., Piccioni, G., Noschese, R., Cicchetti, A., Plainaki, C., Olivieri, A., ONeill, M. E., Turrini, D., Stefani, S., Sordini, R. & Amoroso, M. 2018 Cluster of cyclones encircling Jupiter’s poles. Nature 555, 216–219.10.1038/nature25491Google Scholar
Dritschel, D. G. 1985 The stability and energetics of corotating uniform vortices. J. Fluid Mech. 157, 95–134.10.1017/S0022112085002324Google Scholar
Dritschel, D. G. 1986 The nonlinear evolution of rotating configurations of uniform vorticity. J. Fluid Mech. 172, 157–182.10.1017/S0022112086001696Google Scholar
Dritschel, D. G. 1988 Contour surgery: a topological reconnection scheme for extended integrations using contour dynamics. J. Comput. Phys. 77, 240–266.10.1016/0021-9991(88)90165-9Google Scholar
Dritschel, D. G. 1995 A general theory for two dimensional vortex interactions. J. Fluid Mech. 293, 269–303.10.1017/S0022112095001716Google Scholar
Dritschel, D. G. 2002 Vortex merger in rotating stratified flows. J. Fluid Mech. 455, 83–101.10.1017/S0022112001007364Google Scholar
Dritschel, D. G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65 (3), 855–874.10.1175/2007JAS2227.1Google Scholar
Dritschel, D. G. & Saravanan, R. 1994 Three-dimensional quasi-geostrophic contour dynamics, with an application to stratospheric vortex dynamics. Q. J. R. Meteorol. Soc. 120, 1267–1297.10.1002/qj.49712051908Google Scholar
Hoskins, B. J., McIntyre, M. E. & Robertson, A. W. 1985 On the use and significance of isentropic potential-vorticity maps. Q. J. R. Meteorol. Soc. 111, 877–946.10.1002/qj.49711147002Google Scholar
Kossin, J. P. & Schubert, W. H. 2001 Mesovortices, polygonal patterns and rapid pressure falls in hurricane-like vortices. J. Atmos. Sci. 58, 2196–2209.10.1175/1520-0469(2001)058<2196:MPFPAR>2.0.CO;22.0.CO;2>Google Scholar
Morel, Y. G. & Carton, X. J. 1994 Multipolar vortices in two-dimensional incompressible flows. J. Fluid Mech. 276, 23–51.10.1017/S0022112094001102Google Scholar
Morikawa, G. K. & Swenson, E. V. 1971 Interacting motion of rectilinear geostrophic vortices. Phys. Fluids 14 (6), 1058–1073.10.1063/1.1693564Google Scholar
Reinaud, J. N. 2019 Three-dimensional quasi-geostrophic vortex equilibria with m-fold symmetry. J. Fluid Mech. 863, 32–59.10.1017/jfm.2018.989Google Scholar
Reinaud, J. N. & Dritschel, D. G. 2002 The merger of vertically offset quasi-geostrophic vortices. J. Fluid Mech. 469, 287–315.10.1017/S0022112002001854Google Scholar
Scott, R. K. & Dritschel, D. G. 2005 Quasi-geostrophic vortices in compressible atmospheres. J. Fluid. Mech. 530, 305–325.10.1017/S002211200500371XGoogle Scholar
Thomson, J. J. 1883 A Treatise of Vortex Rings. MacMillan and Co.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-scale Circulation. Cambridge University Press.10.1017/CBO9780511790447Google Scholar
Williams, G. P. 1978 Planetary circulations: 1. Barotropic representation of Jovian and terrestrial turbulence. J. Atmos. Sci. 35, 1399–1424.10.1175/1520-0469(1978)035<1399:PCBROJ>2.0.CO;22.0.CO;2>Google Scholar