Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T06:50:13.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of plane Poiseuille–Couette flow in a fluid layer overlying a porous layer

Published online by Cambridge University Press:  03 August 2017

Ting-Yueh Chang ,
Falin Chen  and
Min-Hsing Chang Open the ORCID record for Min-Hsing Chang [Opens in a new window]
Ting-Yueh Chang
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei, 106, Taiwan
Falin Chen
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei, 106, Taiwan
Min-Hsing Chang*
Affiliation:
Department of Mechanical Engineering, Tatung University, Taipei, 104, Taiwan
*
†Email address for correspondence: mhchang@ttu.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper performs a linear stability analysis to investigate the stability of plane Poiseuille–Couette flow in a fluid layer overlying a porous medium saturated with the same fluid. The effect of superimposed Couette flow on the associated Poiseuille flow in such a two-layer system is explored carefully. 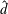The result shows that the presence of Couette flow may destabilize the Poiseuille flow at small depth ratio $\hat{d}$, defined by the ratio of the depth of the fluid layer to the depth of the porous layer, and induce a tri-modal structure to the neutral curves. At moderate 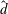$\hat{d}$, the Couette component generally produces a stabilization effect on the flow. When the velocity of the upper moving wall is large enough, a bi-modal behaviour of the neutral curves appears and a shift of instability mode occurs from the long-wave fluid-layer mode to the porous-layer mode with higher wavenumber. These stability characteristics are remarkably different from those of the plane Poiseuille–Couette flow in a single fluid layer in that the flow becomes absolutely stable when the wall velocity is over 70 % of the maximum velocity of the Poiseuille component of flow. The stability of pure Couette flow in such a two-layer system is also studied. It is found that the flow is still absolutely stable with respect to infinitesimal disturbances, which is the same as the stability characteristic of a single-layer plane Couette flow.

JFM classification

Instability: Absolute/convective instability Flow Control: Instability control Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 376 - 395
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bars, M. L. & Worster, M. G. 2006 Interfacial conditions between a pure fluid and a porous medium: implications for binary alloy solidification. J. Fluid Mech. 550, 149–173.Google Scholar
Beavers, G. S. & Joseph, D. D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207.CrossRefGoogle Scholar
Bergström, L. B. 2005 Nonmodal growth of three-dimensional disturbances on plane Couette–Poiseuille flows. Phys. Fluids 17, 014105.Google Scholar
Chang, M.-H. 2005 Thermal convection in superposed fluid and porous layers subjected to a horizontal plane Couette flow. Phys. Fluids 17, 064106.Google Scholar
Chang, M.-H. 2006 Thermal convection in superposed fluid and porous layers subjected to a plane Poiseuille flow. Phys. Fluids 18, 035104.CrossRefGoogle Scholar
Chang, M.-H., Chen, F. & Straughan, B. 2006 Instability of Poiseuille flow in a fluid overlying a porous layer. J. Fluid Mech. 564, 287–303.Google Scholar
Cowley, S. J. & Smith, F. T. 1985 On the stability of Poiseuille–Couette flow: a bifurcation from infinity. J. Fluid Mech. 156, 83–100.Google Scholar
Deepu, P., Anand, P. & Basu, S. 2015 Stability of Poiseuille flow in a fluid overlying an anisotropic and inhomogeneous porous layer. Phys. Rev. E 92, 023009.Google Scholar
Dongarra, J. J., Straughan, B. & Walker, D. W. 1996 Chebyshev tau-QZ algorithm methods for calculating spectra of hydrodynamic stability problems. Appl. Numer. Maths 22, 399–435.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Guha, A. & Frigaard, I. A. 2010 On the stability of plane Couette–Poiseuille flow with uniform crossflow. J. Fluid Mech. 656, 417–447.Google Scholar
Hains, F. D. 1967 Stability of plane Couette–Poiseuille flow. Phys. Fluids 10, 2079–2080.Google Scholar
Hains, F. D. 1971 Stability of plane Couette–Poiseuille flow with uniform crossflow. Phys. Fluids 14, 1620–1623.Google Scholar
Hill, A. A. & Straughan, B. 2008 Poiseuille flow in a fluid overlying a porous medium. J. Fluid Mech. 603, 137–149.Google Scholar
Hill, A. A. & Straughan, B. 2009 Poiseuille flow in a fluid overlying a highly porous material. Adv. Water Resour. 32, 1609–1614.Google Scholar
Kumar, A. A. P., Goyal, H., Banerjee, T. & Bandyopadhyay, D. 2013 Instability modes of a two-layer Newtonian plane Couette flow past a porous medium. Phys. Rev. E 87, 063003.Google Scholar
Liu, R., Liu, Q. S. & Zhao, S. C. 2008 Instability of plane Poiseuille flow in a fluid-porous system. Phys. Fluids 20, 104105.Google Scholar
Lyubimova, T. P., Lyubimov, D. V., Baydina, D. T., Kolchanova, E. A. & Tsiberkin, K. B. 2016 Instability of plane-parallel flow of incompressible liquid over a saturated porous medium. Phys. Rev. E 94, 013104.Google Scholar
Moyers-Gonzalez, M. & Frigaard, I. 2010 The critical wall velocity for stabilization of plane Couette–Poiseuille flow of viscoelastic fluids. J. Non-Newtonian Fluid Mech. 165, 441–447.CrossRefGoogle Scholar
Nouar, C. & Frigaard, I. 2009 Stability of Couette–Poiseuille flow of shear-thinning fluid. Phys. Fluids 21, 064104.Google Scholar
Özgen, S., Dursunkaya, Z. & Ebrinc, A. A. 2007 Heat transfer effects on the stability of low velocity plane Couette–Poiseuille flow. Heat Mass Transfer 43, 1317–1328.Google Scholar
Potter, M. C. 1966 Stability of plane Couette–Poiseuille flow. J. Fluid Mech. 24, 609–619.Google Scholar
Reynolds, W. C. & Potter, M. C. 1967 Finite-amplitude instability of parallel shear flows. J. Fluid Mech. 27, 465–492.Google Scholar
Savenkov, I. V. 2008 Features of wave packets in the plane Poiseuille–Couette flow. Comput. Math. Math. Phys. 48, 1203–1209.Google Scholar
Straughan, B. 2002 Effect of property variation and modelling on convection in a fluid overlying a porous layer. Intl J. Numer. Anal. Meth. Geomech. 26, 75–97.Google Scholar
Tran, T. D. & Suslov, S. A. 2009 Stability of plane Poiseuille–Couette flows of a piezo-viscous fluid. J. Non-Newton. Fluid Mech. 156, 139–149.Google Scholar