Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T07:59:17.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of wall bounded, shear flows of dense granular materials: the role of the Couette gap, the wall velocity and the initial concentration

Published online by Cambridge University Press:  22 February 2016

C. Varsakelis  and
M. V. Papalexandris
C. Varsakelis*
Affiliation:
Institute of Mechanics, Materials and Civil Engineering, Université catholique de Louvain, Belgium
M. V. Papalexandris
Affiliation:
Institute of Mechanics, Materials and Civil Engineering, Université catholique de Louvain, Belgium
*
†Email address for correspondence: christos.varsakelis@uclouvain.be
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, the stability of a plane, unidirectional Couette flow of a dense granular material is investigated via the means of a normal mode stability analysis. Our studies are based on a continuum mechanical model for the flows of interest coupled with the constitutive expressions for the normal and the shear stresses of the granular material induced by the 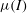${\it\mu}(I)$-rheology. According to our analysis, both the Couette gap and the wall velocity play a destabilizing role in the flows of interest as opposed to the initial concentration that acts as stabilizer. For sufficiently high Couette gaps and wall velocities, unstable modes are recovered. The predicted instability manifests itself through shear-induced dilatancy that, in turn, engenders particle migration and the formation of bulbs, similar to the ones that have been acquired through molecular dynamics simulations.

JFM classification

Complex Fluids: Complex Fluids Granular media: Granular media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 384 - 413
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M., Arakeri, V. H., Nott, P. R., Goddard, J. D. & Herrmann, H. J. 2005 Instability-induced ordering, universal unfolding and the role of gravity in granular Couette flow. J. Fluid Mech. 523, 277–306.Google Scholar
Alam, M. & Nott, P. R. 1997 The influence of friction on the stability of unbounded granular shear flow. J. Fluid Mech. 343, 267–301.Google Scholar
Alam, M. & Nott, P. R. 1998 Stability of plane Couette flow of a granular material. J. Fluid Mech. 377, 99–136.Google Scholar
Alam, M. & Shukla, P. 2013 Nonlinear stability, bifurcation and vortical patterns in three-dimensional granular plane Couette flow. J. Fluid Mech. 716, 349–413.Google Scholar
Babić, M. 1993 On the stability of rapid shear flows. J. Fluid Mech. 254, 223–256.CrossRefGoogle Scholar
Baer, M. R. & Nunziato, J. W. 1986 A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reactive granular materials. Intl J. Multiphase Flow 12, 861–889.Google Scholar
Barker, T., Schaeffer, D. G., Bohorquez, P. & Gray, J. M. N. T. 2015 Well-posed and ill-posed behaviour of the ${\it\mu}(i)$ -rheology for granular flow. J. Fluid Mech. 779, 794–818.Google Scholar
Bdzil, J. B., Menikoff, R., Son, S. F., Kapila, A. K. & Stewart, D. S. 1999 Two-phase modelling of deflagration-to-detonation transition in granular materials: a critical examination of modelling issues. Phys. Fluids 11, 378–492.Google Scholar
Carroll, M. M. & Holt, A. C. 1972 Static and dynamic pore-collapse relations for ductile porous materials. J. Appl. Phys. 43, 1626–1635.Google Scholar
Chen, W.-Y., Lai, J.-Y. & Young, D. L. 2010 Stability analysis of unbounded uniform dense granular shear flow based on a viscoplastic constitutive law. Phys. Fluids 22, 113304.Google Scholar
Chen, W.-Y., Lai, J.-Y. & Young, D. L. 2012 Stability analysis of unbounded uniform shear flows of dense, slightly inelastic spheres based on a frictional-kinetic theory. Intl J. Multiphase Flow 38 (1), 27–34.CrossRefGoogle Scholar
Chorin, A. J. & Marsden, J. E. 2000 A Mathematical Introduction to Fluid Mechanics. Springer.Google Scholar
Cochran, M. T. & Powers, J. M. 2008 Computation of compaction in compressible granular material. Mech. Res. Commun. 35, 96–103.CrossRefGoogle Scholar
Conway, S. L. & Glasser, B. J. 2004 Density waves and coherent structures in granular Couette flows. Phys. Fluids 16, 509–529.Google Scholar
Conway, S. L., Liu, X. & Glasser, B. J. 2006 Instability-induced clustering and segregation in high-shear couette flows of model granular materials. Chem. Engng Sci. 61 (19), 6404–6423.Google Scholar
da Cruz, F. S., Prochnow, M., Roux, J. N. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulations of plane shear flows. Phys. Rev. E 72, 021309.Google ScholarPubMed
Dongarra, J. J., Straughanb, B. & Walker, D. W. 1996 Chebyshev tau-QZ algorithm methods for calculating spectra of hydrodynamic stability problems. Appl. Numer. Maths 22, 399–434.Google Scholar
Drazin, P. G. & Reid, W. H. 2011 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Drew, A. D. & Passman, S. L. 1999 Theory of Multicomponent Fluids. Springer.Google Scholar
Dunn, J. E. & Serrin, J. B. 1985 On the thermo-mechanics of interstitial working. Arch. Rat. Mech. Anal. 88, 95–133.Google Scholar
Elban, W. L. & Chiarito, M. A. 1986 Quasi-static compaction study of coarse HMX explosive. Powder Technol. 46, 181–193.Google Scholar
Fang, C. 2008a Modeling dry granular mass flows as elasto-visco-hypoplastic continua with microstructural effects. I. Thermodynamically consistent constitutive model. Acta Mechanica 197, 173–189.Google Scholar
Fang, C. 2008b Modeling dry granular mass flows as elasto-visco-hypoplastic continua with microstructural effects. II. Numerical simulations of benchmark flow problems. Acta Mechanica 197, 191–209.Google Scholar
Fang, C., Wang, Y. & Hutter, K. 2006a A thermo-mechanical continuum theory with internal length for cohesionless granular materials Part II. Non-equilibrium postulates and numerical simulations of simple shear, plane Poiseuille and gravity driven problems. Contin. Mech. Thermodyn. 17, 577–607.Google Scholar
Fang, C., Wang, Y. & Hutter, K. 2006b A thermo-mechanical continuum theory with internal length for cohesionless granular materials. Contin. Mech. Thermodyn. 17, 577–607.CrossRefGoogle Scholar
Forterre, Y. 2006 Kapiza waves as a test for three-dimensional granular flow rheology. J. Fluid Mech. 563, 123–132.Google Scholar
Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40, 1–24.CrossRefGoogle Scholar
Goddard, J. D. 2003 Material instability in complex fluids. Annu. Rev. Fluid Mech. 35 (1), 113–133.CrossRefGoogle Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267–293.Google Scholar
Goodman, M. A. & Cowin, S. C. 1972 A continuum theory for granular materials. Arch. Rat. Mech. Anal. 44, 249–266.Google Scholar
Gudhe, R., Yalamanchili, R. C. & Rajagopal, K. R. 1994 Flow of granular materials down a vertical pipe. Powder Technol. 81, 65–73.Google Scholar
Hale, N. & Trefethen, N. 2014 Chebfun Guide. Pafnuty Publications.Google Scholar
Henann, D. K. & Kamrin, K. 2013 A predictive, size-dependent continuum model for dense granular flows. Proc. Natl Acad. Sci. USA 110, 6730–6735.Google Scholar
Hopkins, M. A. & Louge, M. 1991 Inelastic microstructure in rapid granular flows of smooth disks. Phys. Fluids A 3, 47–57.Google Scholar
Huang, W. Z. & Sloan, D. M. 1994 The pseudo-spectral method for solving differential eigenvalue problems. J. Comput. Phys. 111, 399–409.Google Scholar
Hutter, K. & Rajagopal, K. R. 1994 On flows of granular materials. Contin. Mech. Thermodyn. 6, 81–139.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985 Kinetic theory for plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 28, 3485–3494.Google Scholar
Jenkins, J. T. & Savage, S. B. 1983 A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 130, 187–202.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441, 727–730.Google Scholar
Josserand, C., Lagrée, P.-Y. & Lhuillier, D. 2004 Stationary shear flows of dense granular materials: A tentative continuum modelling. Eur. Phys. J. E 14, 127–135.Google Scholar
Josserand, C., Lagrée, P.-Y. & Lhuillier, D. 2006 Granular pressure and the thickness of a layer jamming on a rough incline. Europhys. Lett. 73, 363–369.Google Scholar
Kapila, A. K., Menikoff, R., Bdzil, J. B., Son, S. F. & Stewart, D. S. 2001 Two-phase modeling of deflagration-to-detonation transition in granular materials: Reduced equations. Phys. Fluids 13, 3002–3024.CrossRefGoogle Scholar
Kirchner, N. 2002 Thermodynamically consistent modelling of abrasive granular materials. I Non-equilibrium theory. Proc. R. Soc. Lond. A 458, 2153–2176.Google Scholar
Kirchner, N. & Teufel, A. 2002 Thermodynamically consistent modelling of abrasive granular materials. II: Thermodynamic equilibrium and applications to steady shear flows. Proc. R. Soc. Lond. A 458, 3053–3077.Google Scholar
Ladyzhenskaya, O. A. 1969 Mathematical Theory of Viscous, Incompressible Flow. Gordon and Breach.Google Scholar
Ladyzhenskaya, O. A. & Solonnikov, V. A. 1978 Some problems of vector analysis and generalized formulations of boundary-value problems for the Navier–Stokes equations. J. Soviet Math. 10, 257–286.Google Scholar
Lagrée, P.-Y., Staron, L. & Popinet, S. 2011 The granular column collapse as a continuum: validity of a two-dimensional Navier–Stokes model with a ${\it\mu}(I)$ -rheology. J. Fluid Mech. 686, 378–408.Google Scholar
Lions, P. L. 1996 Mathematical Topics in Fluid Mechanics, Volume 1: Incompressible Models. Oxford Press.Google Scholar
Lowe, C. A. & Greenaway, M. W. 2005 Compaction processes in granular beds composed of different particle sizes. J. Appl. Phys. 98, 123519.CrossRefGoogle Scholar
Lun, C. K. K., Savage, S. B., Jeffrey, D. J. & Chepurniy, N. 1984 Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flow field. J. Fluid Mech. 140, 223–256.Google Scholar
Málek, J. & Rajagopal, K. R. 2006 On the modeling of inhomogeneous incompressible fluid-like bodies. Mech. Mater. 38 (3), 233–242.CrossRefGoogle Scholar
Massoudi, M. 2007 Boundary conditions in mixture theory and in CFD applications of higher order models. Comput. Maths Applics. 53, 156–167.Google Scholar
Massoudi, M. & Mehrabadi, M. M. 2001 A continuum model for granular materials: Considering dilatancy and the Mohr-Coulomb criterion. Acta Mechanica 152, 121–138.CrossRefGoogle Scholar
Massoudi, M. & Phuoc, T. X. 2005 Numerical solution to the shearing flow of granular materials between two plates. Intl J. Non-Linear Mech. 40, 1–9.Google Scholar
MiDi, GDR 2004 On dense granular flow. Eur. Phys. J. E 14, 341–365.CrossRefGoogle Scholar
Nott, P. R., Alam, M., Agrawal, K., Jackson, R. & Sundaresan, S. 1999 The effect of boundaries on the plane Couette flow of granular materials: a bifurcation analysis. J. Fluid Mech. 397, 203–229.Google Scholar
Orszag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–703.Google Scholar
Ottino, J. M. & Khakhar, D. V. 2000 Mixing and segregation of granular materials. Annu. Rev. Fluid Mech. 32, 55–91.Google Scholar
Papalexandris, M. V. 2004 A two-phase model for compressible granular flows based on the theory of irreversible processes. J. Fluid Mech. 517, 103–112.Google Scholar
Passman, S. L., Nunziato, J. W. & Bailey, P. B. 1986 Shearing motion of a fluid-saturated granular material. J. Rheol. 20, 167–192.Google Scholar
Passman, S. L., Thomas, J. P. J., Bailey, P. B. & Thomas, J. W. 1980 Shearing flows of granular materials. J. Engng Mech. Div. ASCE 39, 885–901.Google Scholar
Powers, J. M. 2004 Two-phase viscous modeling of compaction of granular materials. Phys. Fluids 16, 2975–2990.Google Scholar
Powers, J. M., Stewart, D. S. & Krier, H. K. 1989 Analysis of steady compaction waves in porous materials. Trans. ASME J. Appl. Mech. 59, 15–24.Google Scholar
Powers, J. M., Stewart, D. S. & Krier, H. K. 1990 Theory of two-phase detonation-Part I: structure. Combust. Flame 80, 280–303.Google Scholar
Savage, S. B. 1979 Gravity flow of cohesionless granular materials in chutes and channels. J. Fluid Mech. 92, 53–96.CrossRefGoogle Scholar
Savage, S. B. 1992 Instability of unbounded uniform granular shear flow. J. Fluid Mech. 241, 109–123.Google Scholar
Savage, S. B. 2008 Free-surface granular flows down heaps. J. Engng Maths 60, 221–240.Google Scholar
Schmid, P. J. & Kytömaa, H. K. 1994 Transient and asymptotic stability of granular shear flow. J. Fluid Mech. 264, 255–275.Google Scholar
Shukla, P. & Alam, M. 2011a Nonlinear stability and patterns in granular plane Couette flow: Hopf and pitchfork bifurcations, and evidence for resonance. J. Fluid Mech. 672, 147–195.Google Scholar
Shukla, P. & Alam, M. 2011b Weakly nonlinear theory of shear-banding instability in a granular plane Couette flow: analytical solution, comparison with numerics and bifurcation. J. Fluid Mech. 666, 204–253.Google Scholar
Svendsen, B. & Hutter, K. 1995 On the thermodynamics of a mixture of isotropic materials with constraints. Intl J. Engng Sci. 1, 2021–2054.Google Scholar
Truesdell, C. 1984 Rational Thermodynamics. Springer.Google Scholar
Truesdell, C. & Noll, W. 1965 The non-linear field theories. In Handbuch der Physik, Bd. III/3, Springer.Google Scholar
Ván, P. 2004 Weakly nonlocal continuum theories of granular media: restrictions from the second law. Intl J. Solids Struct. 41, 5921–5927.Google Scholar
Varsakelis, C. 2015 Gibbs free energy and integrability of continuum models for granular media at equilibrium. Contin. Mech. Thermodyn. 27, 495–498.Google Scholar
Varsakelis, C., Monsorno, D. & Papalexandris, M. V. 2015 Projection methods for two-velocity, two-pressure models for flows of heterogeneous mixtures. Comput. Maths Applics. 70, 1024–1045.Google Scholar
Varsakelis, C. & Papalexandris, M. V. 2010 The equilibrium limit of a constitutive model for two-phase granular mixtures and its numerical approximation. J. Comput. Phys. 229, 4183–4207.Google Scholar
Varsakelis, C. & Papalexandris, M. V. 2011 Low-Mach-number asymptotics for two-phase flows of granular materials. J. Fluid Mech. 669, 472–497.Google Scholar
Varsakelis, C. & Papalexandris, M. V. 2014a Existence of solutions to a continuum model for hydrostatics of fluid-saturated granular materials. Appl. Maths Lett. 35, 77–81.CrossRefGoogle Scholar
Varsakelis, C. & Papalexandris, M. V. 2014b A numerical method for two-phase flows of dense granular mixtures. J. Comput. Phys. 257, 737–756.Google Scholar
Varsakelis, C. & Papalexandris, M. V. 2015a Numerical simulation of subaqueous chute flows of granular materials. Eur. Phys. J. E 28, 40.Google Scholar
Varsakelis, C. & Papalexandris, M. V. 2015b Stability analysis of Couette flows of spatially inhomogeneous complex fluids. Proc. R. Soc. Lond. A 471, 20150529.Google Scholar
Wang, C. H., Jackson, R. & Sundaresan, S. 1996 Stability of bounded rapid shear flows of a granular material. J. Fluid Mech. 308, 31–62.Google Scholar
Wang, Y. & Hutter, K. 1999a A constitutive model of multiphase mixtures and its application in shearing flows of saturated solid-fluid mixtures. Granul. Matt. 73, 163–181.Google Scholar
Wang, Y. & Hutter, K. 1999b A constitutive theory of fluid-saturated granular materials and its application in gravitational flows. Rheol. Acta 38, 214–223.Google Scholar
Wang, Y. & Hutter, K. 1999c Shearing flows in a Goodman–Cowin type granular material-theory and numerical results. Particul. Sci. Technol. 17, 97–124.Google Scholar
Wang, Y. & Hutter, K. 2001 Granular material theories revisited. In Geomorphological Fluid Mechanics (ed. Balmforth, N. J. & Provenzale, A.), Lecture Notes in Physics, vol. 582, pp. 79–107. Springer.CrossRefGoogle Scholar