Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T02:00:57.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Stabilizing effect of optimally amplified streaks in parallel wakes

Published online by Cambridge University Press:  13 December 2013

Gerardo Del Guercio ,
Carlo Cossu Open the ORCID record for Carlo Cossu [Opens in a new window]  and
Gregory Pujals
Gerardo Del Guercio
Affiliation:
CNRS – Institut de Mécanique des Fluides de Toulouse (IMFT), Allée du Professeur Camille Soula, F-31400 Toulouse, France PSA Peugeot Citroën, Centre Technique de Velizy, 2 Route de Gisy, 78943 Vélizy-Villacoublay CEDEX, France
Carlo Cossu*
Affiliation:
CNRS – Institut de Mécanique des Fluides de Toulouse (IMFT), Allée du Professeur Camille Soula, F-31400 Toulouse, France
Gregory Pujals
Affiliation:
PSA Peugeot Citroën, Centre Technique de Velizy, 2 Route de Gisy, 78943 Vélizy-Villacoublay CEDEX, France
*
†Email address for correspondence: carlo.cossu@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that optimal perturbations artificially forced in parallel wakes can be used to completely suppress the absolute instability and to reduce the maximum temporal growth rate of the inflectional instability. To this end we compute optimal transient energy growths of stable streamwise uniform perturbations supported by a parallel wake for a set of Reynolds numbers and spanwise wavenumbers. The maximum growth rates are shown to be proportional to the square of the Reynolds number and to increase with spanwise wavelengths with sinuous perturbations slightly more amplified than varicose ones. Optimal initial conditions consist of streamwise vortices and the optimally amplified perturbations are streamwise streaks. Families of nonlinear streaky wakes are then computed by direct numerical simulation using optimal initial vortices of increasing amplitude as initial conditions. The stabilizing effect of nonlinear streaks on temporal and spatiotemporal growth rates is then determined by analysing the linear impulse response supported by the maximum amplitude streaky wakes profiles. This analysis reveals that at 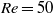$\mathit{Re}= 50$, streaks of spanwise amplitude 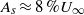${A}_{s} \approx 8\hspace{0.167em} \% {U}_{\infty } $ can completely suppress the absolute instability, converting it into a convective instability. The sensitivity of the absolute and maximum temporal growth rates to streak amplitudes is found to be quadratic, as has been recently predicted. As the sensitivity to two-dimensional (2D, spanwise uniform) perturbations is linear, three-dimensional (3D) perturbations become more effective than the 2D ones only at finite amplitudes. Concerning the investigated cases, 3D perturbations become more effective than the 2D ones for streak amplitudes ${A}_{s} \gtrsim 3\hspace{0.167em} \% {U}_{\infty } $ in reducing the maximum temporal amplification and 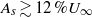${A}_{s} \gtrsim 12\hspace{0.167em} \% {U}_{\infty } $ in reducing the absolute growth rate. However, due to the large optimal energy growths they experience, 3D optimal perturbations are found to be much more efficient than 2D perturbations in terms of initial perturbation amplitudes. Despite their lower maximum transient amplification, varicose streaks are found to be always more effective than sinuous ones in stabilizing the wakes, in accordance with previous findings.

JFM classification

Instability: Absolute/convective instability Flow Control: Flow Control Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 739 , 25 January 2014 , pp. 37 - 56
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, P., Berggren, M. & Henningson, D. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11 (1), 134–150.Google Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.Google Scholar
Bearman, P. W. & Owen, J. C. 1998 Reduction of bluff-body drag and suppression of vortex shedding by the introduction of wavy separation lines. J. Fluids Struct. 12 (1), 123–130.CrossRefGoogle Scholar
Bers, A. 1983 Space–time evolution of plasma instabilities: absolute and convective. In Handbook of Plasma Physics, vol. 1 (ed. Rosenbluth, M. N. & Sagdeev, R. Z.), pp. 451–517. North-Holland.Google Scholar
Brandt, L., Cossu, C., Chomaz, J.-M., Huerre, P. & Henningson, D. S. 2003 On the convectively unstable nature of optimal streaks in boundary layers. J. Fluid Mech. 485, 221–242.Google Scholar
Choi, H., Jeon, W. P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Chomaz, J. M., Huerre, P. & Redekopp, L. G. 1988 Bifurcations to local and global modes in spatially developing flows. Phys. Rev. Lett. 60, 25–28.Google Scholar
Cossu, C. & Brandt, L. 2002 Stabilization of Tollmien–Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 14, L57–L60.Google Scholar
Cossu, C. & Brandt, L. 2004 On Tollmien–Schlichting waves in streaky boundary layers. Eur. J. Mech. B 23, 815–833.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large-scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.Google Scholar
Darekar, R. M. & Sherwin, S. J. 2001 Flow past a square-section cylinder with a wavy stagnation face. J. Fluid Mech. 426 (1), 263–295.Google Scholar
Delbende, I. & Chomaz, J.-M. 1998 Nonlinear convective/absolute instabilities of parallel two-dimensional wakes. Phys. Fluids 10, 2724–2736.Google Scholar
Delbende, I., Chomaz, J.-M. & Huerre, P. 1998 Absolute and convective instabilities in the Batchelor vortex: a numerical study of the linear impulse response. J. Fluid Mech. 355, 229–254.Google Scholar
Fransson, J., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilization of Tollmien–Schlichting waves by finite amplitude streaks. Phys. Fluids 17, 054110.Google Scholar
Fransson, J., Talamelli, A., Brandt, L. & Cossu, C. 2006 Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 96, 064501.Google Scholar
Gustavsson, L. H. 1991 Energy growth of three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 224, 241–260.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Huerre, P. & Rossi, M. 1998 Hydrodynamic instabilities in open flows. In Hydrodynamic and Nonlinear Instabilities (ed. Godrèche, C. & Manneville, P.), pp. 81–294. Cambridge University Press.CrossRefGoogle Scholar
Hwang, Y. & Choi, H. 2006 Control of absolute instability by basic-flow modification in a parallel wake at low Reynolds number. J. Fluid Mech. 560, 465–475.Google Scholar
Hwang, Y. & Cossu, C. 2010 Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.Google Scholar
Hwang, Y., Kim, J. & Choi, H. 2013 Stabilization of absolute instability in spanwise wavy two-dimensional wakes. J. Fluid Mech. 727, 346–378.Google Scholar
Kim, J. & Choi, H. 2005 Distributed forcing of flow over a circular cylinder. Phys. Fluids 39, 033103.Google Scholar
Kim, J., Hahn, S., Kim, J., Lee, D., Choi, J., Jeon, W. & Choi, H. 2004 Active control of turbulent flow over a model vehicle for drag reduction. J. Turbul. 5 (19).CrossRefGoogle Scholar
Lauga, E. & Cossu, C. 2005 A note on the stability of slip channel flows. Phys. Fluids 17, 088106.CrossRefGoogle Scholar
Lombardi, M., Caulfield, C. P., Cossu, C., Pesci, A. I. & Goldstein, R. E. 2011 Growth and instability of a laminar plume in a strongly stratified environment. J. Fluid Mech. 671, 184–206.CrossRefGoogle Scholar
Monkewitz, P. A. 1988 The absolute and convective nature of instability in two-dimensional wakes at low Reynolds numbers. Phys. Fluids 31, 999–1006.Google Scholar
Nayfeh, A. H. & Mook, D. T. 1979 Nonlinear Oscillations. Wiley-Interscience.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in turbulent Couette and Poiseuille flows. C. R. Méc. 339, 1–5.Google Scholar
Park, H., Lee, D., Jeon, W. P., Hahn, S., Kim, J. & Choi, H. 2006 Drag reduction in flow over a two-dimensional bluff body with a blunt trailing edge using a new passive device. J. Fluid Mech. 563, 389–414.Google Scholar
Pradeep, D. S. & Hussain, F. 2006 Transient growth of perturbations in a vortex column. J. Fluid Mech. 550, 251–288.CrossRefGoogle Scholar
Pralits, J. O., Giannetti, F. & Brandt, L. 2013 Three-dimensional instability of the flow around a rotating circular cylinder. J. Fluid Mech. 730, 5–18.CrossRefGoogle Scholar
Pujals, G., Depardon, S. & Cossu, C. 2010 Drag reduction of a 3D bluff body using coherent streamwise streaks. Exp. Fluids 49 (5), 1085–1094.CrossRefGoogle Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.Google Scholar
Reddy, S. C., Schmid, P. J., Baggett, J. S. & Henningson, D. S. 1998 On the stability of streamwise streaks and transition thresholds in plane channel flows. J. Fluid Mech. 365, 269–303.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Tanner, M. 1972 A method for reducing the base drag of wings with blunt trailing edges. Aeronaut. Q. 23, 15–23.Google Scholar
Zdravkovich, M. M. 1981 Review and classification of various aerodynamic and hydrodynamic means for suppressing vortex shedding. J. Wind Engng Ind. Aerodyn. 7, 145–189.Google Scholar