Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T17:19:28.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Stable equilibrium configurations of an oblate capsule in simple shear flow

Published online by Cambridge University Press:  24 February 2016

C. Dupont ,
F. Delahaye ,
D. Barthès-Biesel  and
A.-V. Salsac
C. Dupont
Affiliation:
Biomechanics and Bioengineering Laboratory (UMR CNRS 7338), Sorbonne Universités, Université de technologie de Compiègne - CNRS, CS 60319, 60203 Compiègne, France Solid Mechanics Laboratory (UMR CNRS 7649), Université Paris-Saclay, Ecole Polytechnique - CNRS, 91128 Palaiseau, France
F. Delahaye
Affiliation:
Biomechanics and Bioengineering Laboratory (UMR CNRS 7338), Sorbonne Universités, Université de technologie de Compiègne - CNRS, CS 60319, 60203 Compiègne, France
D. Barthès-Biesel
Affiliation:
Biomechanics and Bioengineering Laboratory (UMR CNRS 7338), Sorbonne Universités, Université de technologie de Compiègne - CNRS, CS 60319, 60203 Compiègne, France
A.-V. Salsac*
Affiliation:
Biomechanics and Bioengineering Laboratory (UMR CNRS 7338), Sorbonne Universités, Université de technologie de Compiègne - CNRS, CS 60319, 60203 Compiègne, France
*
†Email address for correspondence: a.salsac@utc.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The objective of the paper is to determine the stable mechanical equilibrium states of an oblate capsule subjected to a simple shear flow, by positioning its revolution axis initially off the shear plane. We consider an oblate capsule with a strain-hardening membrane and investigate the influence of the initial orientation, capsule aspect ratio 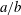$a/b$, viscosity ratio 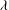${\it\lambda}$ between the internal and external fluids and the capillary number 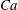$Ca$ which compares the viscous to the elastic forces. A numerical model coupling the finite element and boundary integral methods is used to solve the three-dimensional fluid–structure interaction problem. For any initial orientation, the capsule converges towards the same mechanical equilibrium state, which is only a function of the capillary number and viscosity ratio. For 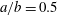$a/b=0.5$, only four regimes are stable when 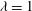${\it\lambda}=1$: tumbling and swinging in the low and medium 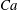$Ca$ range (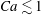$Ca\lesssim 1$), regimes for which the capsule revolution axis is contained within the shear plane; then wobbling during which the capsule experiences precession around the vorticity axis; and finally rolling along the vorticity axis at high capillary numbers. When 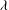${\it\lambda}$ is increased, the tumbling-to-swinging transition occurs for higher 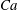$Ca$; the wobbling regime takes place at lower $Ca$ values and within a narrower $Ca$ range. For 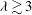${\it\lambda}\gtrsim 3$, the swinging regime completely disappears, which indicates that the stable equilibrium states are mainly the tumbling and rolling regimes at higher viscosity ratios. We finally show that the 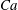$Ca$–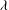${\it\lambda}$ phase diagram is qualitatively similar for higher aspect ratio. Only the 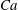$Ca$-range over which wobbling is stable increases with 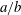$a/b$, restricting the stability ranges of in- and out-of-plane motions, although this phenomenon is mainly visible for viscosity ratios larger than 1.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Capsule/cell dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 738 - 757
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abkarian, M., Faivre, M. & Viallat, A. 2007 Swinging of red blood cells under shear flow. Phys. Rev. Lett. 98, 188302.Google Scholar
Abkarian, M. & Viallat, A. 2008 Vesicles and red blood cells in shear flow. Soft Matt. 4, 653–657.Google Scholar
Bagchi, P. & Kalluri, R. M. 2009 Dynamics of nonspherical capsules in shear flow. Phys. Rev. E 80 (1), 016307.Google Scholar
Barthès-Biesel, D., Walter, J. & Salsac, A.-V. 2010 Flow-induced deformation of artificial capsules. In Computational Hydrodynamics of Capsules and Biological Cells, pp. 35–70. Taylor & Francis.Google Scholar
Bhujbal, S. V., de Vos, P. & Niclou, S. P. 2014 Drug and cell encapsulation: alternative delivery options for the treatment of malignant brain tumors. Adv. Drug Deliv. Rev. 67–68, 142–153.Google Scholar
Bitbol, M. 1986 Red blood cell orientation in orbit $\text{C}=0$ . Biophys. J. 49, 1055–1068.CrossRefGoogle Scholar
Chang, K. S. & Olbricht, W. L. 1993 Experimental studies of the deformation and breakup of a synthetic capsule in steady and unsteady simple shear flow. J. Fluid Mech. 250, 609–633.CrossRefGoogle Scholar
Chang, T. M. S. 2003 Future generations of red blood cell substitutes. J. Intl Med. 253, 527–535.Google Scholar
Clayton, H. A., James, R. F. L. & London, N. J. M. 1993 Islet microencapsulation: a review. Acta Diabetol. 30, 181–189.Google Scholar
Cordasco, D. & Bagchi, P. 2013 Orbital drift of capsules and red blood cells in shear flow. Phys. Fluids 25, 091902.Google Scholar
Dupire, J., Socol, M. & Viallat, A. 2012 Full dynamics of a red blood cell in shear flow. Proc. Natl Acad. Sci. USA 109 (51), 20808–20813.CrossRefGoogle ScholarPubMed
Dupont, C., Salsac, A.-V. & Barthès-Biesel, D. 2013 Off-plane motion of a prolate capsule in shear flow. J. Fluid Mech. 721, 180–198.Google Scholar
Fischer, T. & Korzeniewski, R. 2013 Threshold shear stress for the transition between tumbling and tank-treading of red blood cells in shear flow: dependence on the viscosity of the suspending medium. J. Fluid Mech. 736, 351–365.Google Scholar
Foessel, E., Walter, J., Salsac, A.-V. & Barthès-Biesel, D. 2011 Influence of internal viscosity on the large deformation and buckling of a spherical capsule in a simple shear flow. J. Fluid Mech. 672, 477–486.Google Scholar
Furlow, B. 2009 Contrast-enhanced ultrasound. Radiol. Technol. 80, 547S–561S.Google Scholar
Goldsmith, H. L. & Marlow, J. 1972 Flow behaviour of erythrocytes. I. Rotation and deformation in dilute suspensions. Proc. R. Soc. Lond. B 182 (1068), 351–384.Google Scholar
Hochmuth, R. M. & Waught, R. E. 1987 Erythrocyte membrane elasticity and viscosity. Annu. Rev. Physiol. 49, 209–219.CrossRefGoogle ScholarPubMed
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Kessler, S., Finken, R. & Seifert, U. 2008 Swinging and tumbling of elastic capsules in shear flow. J. Fluid Mech. 605, 207–226.CrossRefGoogle Scholar
Klöppel, T.2012 A finite element model for the human red blood cell. PhD thesis, Technische Universität München.Google Scholar
Le, D. V. & Tan, Z. 2010 Large deformation of liquid capsules enclosed by thin shells immersed in the fluid. J. Comput. Phys. 229, 4097–4116.Google Scholar
Ma, G. & Su, Z.-G. 2013 Microspheres and Microcapsules in Biotechnology: Design, Preparation and Applications. Pan Stanford Publishing.Google Scholar
MacMeccan, R., Clausen, J. R., Neitzel, G. P. & Aidun, C. K. 2009 Simulating deformable particle suspensions using a coupled lattice–Boltzmann and finite-element method. J. Fluid. Mech. 618, 13–39.Google Scholar
Mohandas, N. & Gallagher, P. G. 2008 Red cell membrane: past, present and future. Blood 112 (10), 3939–3948.Google Scholar
Omori, T., Imai, Y., Yamaguchi, T. & Ishikawa, T. 2012 Reorientation of a nonspherical capsule in creeping shear flow. Phys. Rev. Lett. 108, 138102(5).CrossRefGoogle ScholarPubMed
Ramanujan, S. & Pozrikidis, C. 1998 Deformation of liquid capsules enclosed by elastic membranes in simple shear flow: large deformations and the effect of capsule viscosity. J. Fluid Mech. 361, 117–143.Google Scholar
Skalak, R., Tozeren, A., Zarda, R. P. & Chien, S. 1973 Strain energy function of red blood cell membranes. Biophys. J. 13, 245–264.Google Scholar
Sui, Y., Low, H. T., Chew, Y. T. & Roy, P. 2008 Tank–treading, swinging, and tumbling of liquid-filled elastic capsules in shear flow. Phys. Rev. E 77 (1), 016310.Google Scholar
Walter, A., Rehage, H. & Leonhard, H. 2001 Shear induced deformation of microcapsules: shape oscillations and membrane folding. Colloid Surf. A 183–185, 123–132.Google Scholar
Walter, J., Salsac, A.-V. & Barthès-Biesel, D. 2011 Ellipsoidal capsules in simple shear flow: prolate versus oblate initial shapes. J. Fluid Mech. 676, 318–347.CrossRefGoogle Scholar
Walter, J., Salsac, A.-V., Barthès-Biesel, D. & Le Tallec, P. 2010 Coupling of finite element and boundary integral methods for a capsule in a Stokes flow. Intl J. Numer. Meth. Engng 83, 829–850.Google Scholar
Wang, Z., Sui, Y., Spelt, P. D. M. & Wang, W. 2013 Three-dimensional dynamics of oblate and prolate capsules in shear flow. Phys. Rev. E 88, 053021.Google Scholar
Yao, W., Wen, Z., Yan, Z., Sun, D., Ka, W., Xie, L. & Chien, S. 2001 Low viscosity Ektacytometry and its validation tested by flow chamber. J. Biomech. 34, 1501–1509.Google Scholar
Yazdani, A. & Bagchi, P. 2013 Influence of membrane viscosity on capsule dynamics in shear flow. J. Fluid Mech. 718, 569–595.Google Scholar

Dupont et al. supplementary movie

Tumbling motion of an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 45°; the capillary number is Ca = 0.01 and the internal to external viscosity ratio λ = 1. The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3 (t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass.

Download Dupont et al. supplementary movie(Video)
Video 16.4 MB

Dupont et al. supplementary movie

Swinging motion of an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 30°; the capillary number is Ca = 0.03 and the internal to external viscosity ratio λ = 1. The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3(t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass.

Download Dupont et al. supplementary movie(Video)
Video 12.7 MB

Dupont et al. supplementary movie

Motion of transition between the swinging and rolling regimes with precession around the vorticity axis for an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 45°; the capillary number is Ca = 0.9 and the internal to external viscosity ratio λ = 1. The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3(t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass.

Download Dupont et al. supplementary movie(Video)
Video 12.7 MB

Dupont et al. supplementary movie

Rolling motion of an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 15°; the capillary number is Ca = 2 and the internal to external viscosity ratio λ = 1.The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3(t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass.

Download Dupont et al. supplementary movie(Video)
Video 6 MB

Dupont et al. supplementary movie

Relaxation to rest of an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane) experiencing a steady rolling regime. The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 15°; the capillary number is Ca = 2 and the internal to external viscosity ratio λ = 1. The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3(t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass. The movie encoding speed was decreased by a factor 20 compared to the other films to enable the visualization of the relaxation phenomenon.

Download Dupont et al. supplementary movie(Video)
Video 268.1 KB