Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Han, Dongrui
Xiong, Jie
Xie, Xiaoyun
and
Lin, Yingtien
2021.
Effects of emergent and submerged rigid vegetation configurations on gravity current dynamics.
Environmental Fluid Mechanics,
Vol. 21,
Issue. 5,
p.
1165.
Dai, Albert
Huang, Yu-Lin
and
Hsieh, Yu-Min
2021.
Gravity currents propagating at the base of a linearly stratified ambient.
Physics of Fluids,
Vol. 33,
Issue. 6,
Marshall, C. R.
Dorrell, R. M.
Dutta, S.
Keevil, G. M.
Peakall, J.
and
Tobias, S. M.
2021.
The effect of Schmidt number on gravity current flows: The formation of large-scale three-dimensional structures.
Physics of Fluids,
Vol. 33,
Issue. 10,
Frantz, Ricardo A.S.
Deskos, Georgios
Laizet, Sylvain
and
Silvestrini, Jorge H.
2021.
High-fidelity simulations of gravity currents using a high-order finite-difference spectral vanishing viscosity approach.
Computers & Fluids,
Vol. 221,
Issue. ,
p.
104902.
Pelmard, Joë
Norris, Stuart
and
Friedrich, Heide
2021.
Turbulent density transport in the mixing layer of an unsteady gravity current.
Advances in Water Resources,
Vol. 154,
Issue. ,
p.
103963.
Adekanye, Damilola
Khan, Amirul
Burns, Alan
McCaffrey, William
Geier, Martin
Schönherr, Martin
and
Dorrell, Robert
2022.
Graphics processing unit accelerated lattice Boltzmann method simulations of dilute gravity currents.
Physics of Fluids,
Vol. 34,
Issue. 4,
Xie, Jiafeng
Hu, Peng
Pähtz, Thomas
He, Zhiguo
and
Cheng, Niansheng
2022.
Fluid-particle interaction regimes during the evolution of turbidity currents from a coupled LES/DEM model.
Advances in Water Resources,
Vol. 163,
Issue. ,
p.
104171.
Cui, Ting
Kamath, Arun
Wang, Weizhi
Han, Duanfeng
and
Bihs, Hans
2022.
Large-eddy simulations of gravity currents in the presence of waves.
Journal of Hydraulic Research,
Vol. 60,
Issue. 5,
p.
770.
Kokkinos, Angelos
and
Prinos, Panagiotis
2022.
Numerical experiments of partial-depth colliding gravity currents using LES.
Environmental Fluid Mechanics,
Vol. 22,
Issue. 5,
p.
1081.
Maggi, Maria Rita
Adduce, Claudia
and
Negretti, Maria Eletta
2022.
Lock-release gravity currents propagating over roughness elements.
Environmental Fluid Mechanics,
Vol. 22,
Issue. 2-3,
p.
383.
Xie, Jiafeng
Hu, Peng
Zhu, Chenlin
Yu, Zhaosheng
and
Pähtz, Thomas
2023.
Turbidity currents propagating down an inclined slope: particle auto-suspension.
Journal of Fluid Mechanics,
Vol. 954,
Issue. ,
Marshall, C. R.
Dorrell, R. M.
Keevil, G. M.
Peakall, J.
and
Tobias, S. M.
2023.
On the role of transverse motion in pseudo-steady gravity currents.
Experiments in Fluids,
Vol. 64,
Issue. 3,
Kokkinos, Angelos
and
Prinos, Panagiotis
2023.
On the dynamics of gravity current motion in a stratified ambient.
Journal of Hydraulic Research,
Vol. 61,
Issue. 5,
p.
703.
Dai, Albert
Huang, Yu-Lin
and
Wu, Ching-Sen
2023.
Energy balances for the collision of gravity currents of equal strengths.
Journal of Fluid Mechanics,
Vol. 959,
Issue. ,
Yuan, Yeping
Han, Dongrui
He, Zhiguo
Xiong, Jie
Zhang, Jiaxin
and
Lin, Yingtien
2023.
Uncertainty of propagation and entrainment characteristics of lock-exchange gravity current.
Environmental Fluid Mechanics,
Vol. 23,
Issue. 1,
p.
19.
Kokkinos, Angelos
and
Prinos, Panagiotis
2023.
Investigation of asymmetric gravity current collision with LES.
Journal of Hydraulic Research,
Vol. 61,
Issue. 6,
p.
893.
Zahtila, Tony
Lam, Wai Kit
Chan, Leon
Sutherland, Duncan
Moinuddin, Khalid
Dai, Albert
Skvortsov, Alex
Manasseh, Richard
and
Ooi, Andrew
2024.
On the propagation of planar gravity currents into a stratified ambient.
Physics of Fluids,
Vol. 36,
Issue. 3,
Yang, Yefeng
Chen, Jiawang
and
Wang, Yin
2024.
Particle plume dispersion with various incident velocities: Particle–fluid interaction regimes from coupled discrete element-large eddy simulations.
Physics of Fluids,
Vol. 36,
Issue. 8,
Bardoel, Stef L.
Cheng, Shyuan
Chamorro, Leonardo P.
and
Fernando, Harindra J.S.
2025.
Gravity currents past thin two-dimensional obstacles.
Journal of Fluid Mechanics,
Vol. 1012,
Issue. ,
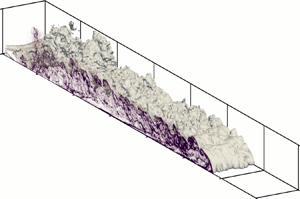
 $Ri_f = 0.2$. It is furthermore observed that the turbulence intensity in all three spatial directions stabilises to satisfy
$Ri_f = 0.2$. It is furthermore observed that the turbulence intensity in all three spatial directions stabilises to satisfy  $\langle u'u' \rangle = 2 \langle v'v' \rangle = 2 \langle w'w' \rangle$, where
$\langle u'u' \rangle = 2 \langle v'v' \rangle = 2 \langle w'w' \rangle$, where  $u', v' \ \text{and} \ w'$ are respectively the streamwise, spanwise and vertical turbulent perturbations of velocity. Finally, a region of statistically stationary TKE is identified once the gradient Richardson number plateaus to a value dependent on the current's propagation approximately 5.5 lock heights backward from the front, where the depth-averaged TKE budget reduces to the balance between the contributions due to shear (P), buoyancy (B) and viscous dissipation
$u', v' \ \text{and} \ w'$ are respectively the streamwise, spanwise and vertical turbulent perturbations of velocity. Finally, a region of statistically stationary TKE is identified once the gradient Richardson number plateaus to a value dependent on the current's propagation approximately 5.5 lock heights backward from the front, where the depth-averaged TKE budget reduces to the balance between the contributions due to shear (P), buoyancy (B) and viscous dissipation  $(\varepsilon)$ as
$(\varepsilon)$ as  $\langle P \rangle _d + \langle B \rangle _d - \langle \varepsilon \rangle _d \approx 0$.
$\langle P \rangle _d + \langle B \rangle _d - \langle \varepsilon \rangle _d \approx 0$.