Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T01:27:48.347Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady approach of unsteady low-Reynolds-number flow past two rotating circular cylinders

Published online by Cambridge University Press:  07 November 2013

Y. Ueda ,
T. Kida  and
M. Iguchi
Y. Ueda*
Affiliation:
Division of Materials Science and Engineering, Graduate School of Engineering, Hokkaido University, Nishi 8, Kita 13, Kita-Ku, Sapporo, Hokkaido 060-8628, Japan
T. Kida
Affiliation:
Division of Mechanical Engineering, Graduate School of Engineering, Osaka Prefecture University, 1–1, Gakuen-Cho, Naka-Ku, Sakai, Osaka 599-8531, Japan
M. Iguchi
Affiliation:
Division of Materials Science and Engineering, Graduate School of Engineering, Hokkaido University, Nishi 8, Kita 13, Kita-Ku, Sapporo, Hokkaido 060-8628, Japan
*
† Email address for correspondence: y-ueda@eng.hokudai.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

The long-time viscous flow about two identical rotating circular cylinders in a side-by-side arrangement is investigated using an adaptive numerical scheme based on the vortex method. The Stokes solution of the steady flow about the two-cylinder cluster produces a uniform stream in the far field, which is the so-called Jeffery’s paradox. The present work first addresses the validation of the vortex method for a low-Reynolds-number computation. The unsteady flow past an abruptly started purely rotating circular cylinder is therefore computed and compared with an exact solution to the Navier–Stokes equations. The steady state is then found to be obtained for 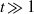$t\gg 1$ with 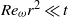${\mathit{Re}}_{\omega } {r}^{2} \ll t$, where the characteristic length and velocity are respectively normalized with the radius 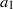${a}_{1} $ of the circular cylinder and the circumferential velocity 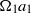${\Omega }_{1} {a}_{1} $. Then, the influence of the Reynolds number 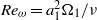${\mathit{Re}}_{\omega } = { a}_{1}^{2} {\Omega }_{1} / \nu $ about the two-cylinder cluster is investigated in the range 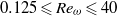$0. 125\leqslant {\mathit{Re}}_{\omega } \leqslant 40$. The convection influence forms a pair of circulations (called self-induced closed streamlines) ahead of the cylinders to alter the symmetry of the streamline whereas the low-Reynolds-number computation (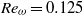${\mathit{Re}}_{\omega } = 0. 125$) reaches the steady regime in a proper inner domain. The self-induced closed streamline is formed at far field due to the boundary condition being zero at infinity. When the two-cylinder cluster is immersed in a uniform flow, which is equivalent to Jeffery’s solution, the streamline behaves like excellent Jeffery’s flow at 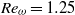${\mathit{Re}}_{\omega } = 1. 25$ (although the drag force is almost zero). On the other hand, the influence of the gap spacing between the cylinders is also investigated and it is shown that there are two kinds of flow regimes including Jeffery’s flow. At a proper distance from the cylinders, the self-induced far-field velocity, which is almost equivalent to Jeffery’s solution, is successfully observed in a two-cylinder arrangement.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Vortex Flows: Vortex Flows Vortex Flows: Vortex shedding Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 736 , 10 December 2013 , pp. 414 - 443
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Professor Emeritus.

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover.Google Scholar
Anderson, C. & Greengard, C. 1985 On vortex methods. SIAM J. Numer. Anal. 22, 413–440.Google Scholar
Badr, H. M. & Dennis, S. C. R. 1985 Time-dependent viscous flow past an impulsively started rotating and translating circular cylinder. J. Fluid Mech. 158, 447–488.CrossRefGoogle Scholar
Bar-Lev, M. & Yang, H. T. 1975 Initial flow field over an impulsively started circular cylinder. J. Fluid Mech. 72, 625–647.Google Scholar
Beale, J. T. & Majda, A. 1985 High order accurate vortex methods with explicit velocity kernels. J. Comput. Phys. 58, 188–208.Google Scholar
Bleistein, N. & Handelsman, R. A. 2010 Asymptotic Expansions of Integrals. Dover.Google Scholar
Caflisch, R. E. 1989 Mathematical analysis of vortex dynamics. In Proceedings of the Workshop on Mathematical Aspects of Vortex Dynamics (ed. Caflisch, R. E.), pp. 1–23. SIAM.Google Scholar
Chen, Y.-M., Ou, Y.-R. & Pearlstein, A. J. 1993 Development of the wake behind a circular cylinder impulsively started into rotatory and rectilinear motion. J. Fluid Mech. 253, 449–484.Google Scholar
Chorin, A. J. 1973 Numerical study of slightly viscous flow. J. Fluid Mech. 57, 785–796.Google Scholar
Cottet, G.-H. & Koumoutsakos, P. D. 2000 Vortex Methods: Theory and Practice. Cambridge University Press.CrossRefGoogle Scholar
Cottet, G.-H., Ould Salihi, M.-L. & El Hamraoui, M. 1999 Multi-purpose regridding in vortex methods. Proc. ESAIM 7, 94–103.Google Scholar
Cottet, G.-H. & Poncet, P. 2003 Advances in direct numerical simulations of 3D wall-bounded flows by vortex-in-cell methods. J. Comput. Phys. 193, 136–158.Google Scholar
Coutanceau, M. & Ménard, C. 1985 Influence of rotation on the near-wake development behind an impulsively started circular cylinder. J. Fluid Mech. 158, 399–446.Google Scholar
Daripa, P. & Palaniappan, D. 2001 Singularity induced exterior and interior Stokes flows. Phys. Fluids 13, 3134–3154.CrossRefGoogle Scholar
Degond, P. & Mas-Gallic, S. 1989 The weighted particle method for convection–diffusion equations, Part 1. The case of an isotropic viscosity. Part 2. The anisotropic case. Math. Comput. 53, 485–525.Google Scholar
Dorrepaal, J. M., O’Neill, M. E. & Banger, K. B. 1984 Two-dimensional Stokes flows with cylinders and line singularities. Mathematika 31, 65–75.CrossRefGoogle Scholar
Elliott, L., Ingham, D. B. & El Bashir, T. B. A. 1995 Stokes flow past two circular cylinders using a boundary element method. Comput. Fluids 24, 787–798.CrossRefGoogle Scholar
Jeffery, G. B. 1920 Plane stress and plane strain in bipolar co-ordinates. Phil. Trans. R. Soc. Lond. A 221, 265–293.Google Scholar
Jeffery, G. B. 1922 The rotation of two circular cylinders in a viscous fluid. Proc. R. Soc. Lond. A 101, 169–174.Google Scholar
Kang, S. 2003 Characteristics of flow over two circular cylinders in a side-by-side arrangement at low Reynolds numbers. Phys. Fluids 15 (9), 2486–2498.Google Scholar
Kaplun, S. & Lagerstrom, P. A. 1957 Asymptotic expansion of Navier–Stokes solutions for small Reynolds numbers. J. Math. Mech. 6, 585–593.Google Scholar
Koumoutsakos, P. 1997 Inviscid axisymmetrization of an elliptical vortex. J. Comput. Phys. 138, 821–857.Google Scholar
Koumoutsakos, P. 2005 Multiscale flow simulations using particles. Annu. Rev. Fluid Mech. 37, 457–487.Google Scholar
Koumoutsakos, P. & Leonard, A. 1995 High-resolution simulations of the flow around an impulsively started cylinder using vortex methods. J. Fluid Mech. 296, 1–38.Google Scholar
Koumoutsakos, P., Leonard, A. & Pépin, F. 1994 Boundary conditions for viscous vortex methods. J. Comput. Phys. 113, 52–61.Google Scholar
Leonard, A. 1985 Computing three-dimensional incompressible flows with vortex elements. Annu. Rev. Fluid Mech. 17, 523–559.CrossRefGoogle Scholar
Nakanishi, M. & Kida, T. 1999 Unsteady low Reynolds number flow past two rotating circular cylinders by a vortex method. In Proceedings of 3rd ASME/JSME Joint Fluids Engineering Conference, FEDSM 99-6816.Google Scholar
Ou, K., Liang, C., Premasuthan, S. & Jameson, A. 2009 High-order spectral difference simulation of laminar compressible flow over two counter-rotating cylinders. In Proceedings of the 27th AIAA Applied Aerodynamics Conference, AIAA 2009-3956.Google Scholar
Ploumhans, P. & Winckelmans, G. S. 2000 Vortex methods for high-resolution simulations of viscous flow past bluff bodies of general geometry. J. Comput. Phys. 165, 354–406.Google Scholar
Proudman, I. & Pearson, J. R. A. 1957 Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 2, 237–262.Google Scholar
Shiels, D. 1998 Simulation of controlled bluff body flow with a viscous vortex method. PhD dissertation, Caltech.Google Scholar
Smith, S. H. 1991 The rotation of two circular cylinders in a viscous fluid. Mathematika 38, 63–66.Google Scholar
Ueda, Y., Sellier, A. & Kida, T. 2005 Analysis of unsteady interactions between cylinders by a vortex method. In Proceedings of ICVFM, CD-ROM.Google Scholar
Ueda, Y., Sellier, A., Kida, T. & Nakanishi, M. 2003 On the low-Reynolds-number flow about two rotating circular cylinders. J. Fluid Mech. 495, 255–281.CrossRefGoogle Scholar
Watson, E. J. 1995 The rotation of two circular cylinders in a viscous fluid. Mathematika 42, 105–126.CrossRefGoogle Scholar
Watson, E. J. 1996 Slow viscous flow past two rotating cylinders. Q. J. Mech. Appl. Maths. 49, 195–215.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Xu, S. J., Zhou, Y. & So, R. M. C. 2003 Reynolds number effects on the flow structure behind two side-by-side cylinders. Phys. Fluids 15, 1214–1219.Google Scholar
Yoon, H. S., Chun, H. H., Kim, J. H. & Park, I. L. R. 2009 Flow characteristics of two rotating side-by-side circular cylinder. Comput. Fluids 38, 466–474.Google Scholar
Yoon, H. S., Kim, J. H., Chun, H. H. & Choi, H. J. 2007 Laminar flow past two rotating circular cylinders in a side-by-side arrangement. Phys. Fluids 19, 128103.Google Scholar