Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T20:30:09.677Z Has data issue: false hasContentIssue false
  • English
  • Français

A Stokesian analysis of a submerged viscous jet impinging on a planar wall

Published online by Cambridge University Press:  28 September 2012

A. M. J. Davis ,
J. H. Kim ,
C. Ceritoglu  and
J. T. Ratnanather
A. M. J. Davis
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, La Jolla, CA 92093-0411, USA
J. H. Kim
Affiliation:
Department of Applied Mathematics and Statistics, The Johns Hopkins University, Baltimore, MD 21218, USA
C. Ceritoglu
Affiliation:
Center for Imaging Science, The Johns Hopkins University, Baltimore, MD 21218, USA
J. T. Ratnanather*
Affiliation:
Center for Imaging Science and Institute for Computational Medicine, Whitaker Biomedical Engineering Institute, The Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: tilak@cis.jhu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The wall pressure and wall shear stress of a submerged viscous jet impinging on an infinite planar wall are derived. The whole creeping flow of semi-infinite extent is generated via distributions on a cylindrical pipe of tangentially and normally directed Stokeslets which are modified to achieve no-slip at the wall in two stages. First the pressure and vorticity jumps associated with the Poiseuille flow upstream in the pipe are readily forced, and then further distributions, of zero density far upstream but with square-root density singularity at the orifice 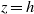$z= h$, are added to achieve no-slip on the pipe wall. Thus the adjustment of the interior pipe flow from its upstream parabolic profile to its exit profile is fully included in – and a major feature of – this creeping flow analysis. The maximum plane wall pressure is always located on the axis 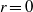$r= 0$, and decreases as 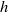$h$ increases to alleviate the obstruction effect of the wall. The interaction of the inflow with the ambient fluid in the neighbourhood of 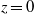$z= 0$ causes the wall stress to rise rapidly to a maximum and then decay with the radial position of this maximum increasing as 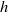$h$ increases. This behaviour is discussed in the context of physiological experiments on auditory sensory hair cells that motivated this study.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Stokesian dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 712 , 10 December 2012 , pp. 531 - 551
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akaike, S. & Nemoto, M. 1998 Potential core of a submerged laminar jet. Trans. ASME: J. Fluids Engng 110, 392–398.Google Scholar
Ashmore, J., Avan, P., Brownell, W. E., Dallos, P., Dierkes, K., Fettiplace, R., Grosh, K., Hackney, C. M., Hudspeth, A. J., Jülicher, F., Lindner, B., Martin, P., Meaud, J., Petit, C., Santos-Sacchi, J. R & Canlon, B. 2010 The remarkable cochlear amplifier. Hear. Res. 266, 1–17.CrossRefGoogle ScholarPubMed
Atkinson, K. E. 1997 The Numerical Solution of Integral Equations of the Second Kind. Cambridge University Press.CrossRefGoogle Scholar
Baydar, E. 1999 Confined impinging air jet at low Reynolds numbers. Exp. Therm. Fluid Sci. 19, 27–33.Google Scholar
Bernard, A., Brizzi, L. E. & Bousgarbies, J. L. 2000 A comparison of flow visualisation and wall pressure measurements for a jet impinging on a plane surface. Exp. Fluids 29, 23–29.Google Scholar
Bouafsoun, A., Othmane, A., Kerkeni, A., Jaffreézic, N. & Ponsonnet, L. 2006 Evaluation of endothelial cell adherence onto collagen and fibronectin: a comparison between jet impingement and flow chamber techniques. Mater. Sci. Engng C 260, 260–266.Google Scholar
Brownell, W. E. 2006 The piezoelectric outer hair cell. In Vertebrate Hair Cells (ed. Eatock, R. A.), pp. 313–347. Springer.Google Scholar
Brundin, L. & Russell, I. J. 1994 Tuned phasic and tonic motile responses of isolated outer hair cells to direct mechanical stimulation of the cell body. Hear. Res. 74, 35–45.CrossRefGoogle Scholar
Burkardt, J. 2010 Generalized Gauss–Laguerre quadrature rules.http://people.sc.fsu.edu/~jburkardt/m_src/gen_laguerre_rule/gen_laguerre_rule.m.Google Scholar
Chen, C., Smye, S. W., Robinson, M. P. & Evans, J. A. 2006 Membrane electroporation theories: a review. Med. Biol. Engng Comput. 44, 5–14.Google Scholar
Davis, A. M. J. 1991 A translating disk in a Sampson flow: pressure-driven flow through concentric holes in parallel walls. Q. J. Mech. Appl. Math. 44, 471–486.CrossRefGoogle Scholar
Davis, A. M. J. 1996 The use of Stokeslets to describe the arbitrary translation of a disk near a plane wall. J. Engng Math. 30, 239–252.CrossRefGoogle Scholar
Davis, A. M. J. 2002 Infinite systems for a biharmonic problem in a rectangle: discussion of non-uniqueness. Proc. R. Soc. Lond. A 459, 409–412.CrossRefGoogle Scholar
Davis, A. M. J. 2003 Rotational effects in Stokes flow: pressure-driven extrusion through an annular hole or concentric holes in parallel walls. J. Engng Math. 46, 227–240.Google Scholar
Davis, A. M. J. 2009 Abel transforms and Green’s functions in axisymmetric Stokes flow. In Theoretical Methods for Micro Scale Viscous Flows (ed. Feuillebois, F. & Sellier, A.), pp. 1–18. Transworld Research Network.Google Scholar
Delves, L. M. & Mohamed, J. L. 1985 Computational Methods for Integral Equations. Cambridge University Press.CrossRefGoogle Scholar
Deshpande, M. D. & Vaishnav, R. N. 1982 Submerged laminar jet impingement on a plane. J. Fluid Mech. 114, 213–236.CrossRefGoogle Scholar
Deshpande, M. D. & Vaishnav, R. N. 1983 Wall stress-distribution due to jet impingement. J. Engng Mech. ASCE 109, 479–493.Google Scholar
Dinklo, T., Meulenberg, C. J. W. & van Netten, S. M. 2007 Frequency-dependent properties of a fluid jet stimulus: calibration, modeling, and application to cochlear hair cell bundles. J. Assoc. Res. Otolaryngology 8, 167–182.Google Scholar
Elhay, S. & Kautsky, J. 1987 Algorithm 655: IQPACK, FORTRAN subroutines for the weights of interpolatory quadrature. ACM Trans. Math. Softw. 13, 399–415.CrossRefGoogle Scholar
Farahbakhsh, N., Zelaya, J. & Narins, P. 2010 Osmotic properties of auditory hair cells in the leopard frog: evidence for water-permeable channels. Hear. Res. 272, 69–84.CrossRefGoogle ScholarPubMed
Fujitani, Y. 2009 Flow around a circular pore of a flat and incompressible fluid-membrane. J. Phys. Soc. Japan 78, 084402.Google Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 2007 Gradshteyn and Ryzhik’s Table of Integrals, Series, and Products, 7th edn (ed. Jeffrey, A & Zwillinger, D.). Academic.Google Scholar
Happel, J. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics. Martinus Nijhoff.CrossRefGoogle Scholar
Housley, G. D., Greenwood, D. & Ashmore, J. F. 1992 Localization of cholinergic and purinergic receptors on outer hair cells isolated from the guinea-pig cochlea. Proc. R. Soc. Lond. B 249, 265–273.Google Scholar
Joseph, D. D. & Sturges, L. 1978 The convergence of biorthogonal series for biharmonic and Stokes flow edge problems. Part 2. SIAM J. Appl. Math. 34, 7–26.Google Scholar
Kong, C.-R., Bursac, N. & Tung, L. 2005 Mechanoelectrical excitation by fluid jets in monolayers of cultured cardiac myocytes. J. Appl. Physiol. 98, 2328–2336.CrossRefGoogle ScholarPubMed
Lauga, E., Brenner, M. P. & Stone, H. A. 2007 Microfluidics: the no-slip boundary condition. In Springer Handbook of Experimental Fluid Mechanics. Springer.Google Scholar
Lin, X., Hume, R. I. & Nuttall, A. L. 1993 Voltage-dependent block by neomycin of the ATP-induced whole-cell current of guinea-pig outer hair-cells. J. Neurophysiol. 70, 1593–1605.Google Scholar
Lucas, S. K. 1995 Evaluating infinite integrals involving products of two Bessel functions of arbitrary order. J. Comput. Appl. Math. 64, 269–282.CrossRefGoogle Scholar
Meleshko, V. V. 1996 Steady Stokes flow in a rectangular cavity. Proc. R. Soc. Lond. A 452, 1999–2002.Google Scholar
Morimoto, N., Raphael, R. M., Nygren, A. & Brownell, W. E. 2002 Excess plasma membrane and effects of ionic amphipaths on mechanics of outer hair cell lateral wall. Am. J. Physiol. Cell Physiol. 282, C1076–C1086.Google Scholar
Nakagawa, T., Akaike, N., Kimitsuki, T., Komune, S. & Arima, T. 1990 ATP-induced current in isolated outer hair cells of guinea pig cochlea. J. Neurophysiol. 63, 1068–1074.CrossRefGoogle ScholarPubMed
Phares, D. J., Smedley, G. T. & Flagan, R. C. 2000a The inviscid impingement of a jet with arbitrary velocity profile. Phys. Fluids 12 (8), 2046–2055.Google Scholar
Phares, D. J., Smedley, G. T. & Flagan, R. C. 2000b The wall shear stress produced by the normal impingement of a jet on a flat surface. J. Fluid Mech. 418, 351–375.Google Scholar
Ratnanather, J. T., Kim, J. H., Zhang, S., Davis, A. M. J. & Lucas, S. K. 2012 IIPBF, a MATLAB toolbox for computing infinite integral of products of two Bessel functions (submitted).Google Scholar
Ratnanather, J. T., Zhi, M., Brownell, W. E. & Popel, A. S. 1996 Measurements and a model of the outer hair cell hydraulic conductivity. Hear. Res. 96, 33–40.Google Scholar
Richards, R. G., ap Gwynn, I., Bundy, K. J. & Rahn, B. A. 1995 Microjet impingement followed by scanning electron microscopy as a qualitative technique to compare cellular adhesion to various biomaterials. Cell Biol. Intl 19, 1015–1024.Google Scholar
Saffman, P. G. 1976 Brownian motion in thin sheets of viscous fluid. J. Fluid Mech. 73, 593–602.Google Scholar
Santos-Sacchi, J., Song, L., Bai, J. P. & Navaratnam, D. 2006 Chloride and the OHC lateral membrane motor. In Auditory Mechanisms: Processes and Models (ed. Nuttall, A. L., Ren, T., Gillespie, P., Grosh, K. & de Boer, E.), pp. 162–165. World Scientific.Google Scholar
Saunders, J. C. & Syzmko, Y. M. 1989 The design, calibration, and use of a water microjet for stimulating hair cell sensory hair bundles. J. Acoust. Soc. Am. 86, 1797–1804.CrossRefGoogle ScholarPubMed
Shankar, P. N. 2005 Eigenfunction expansions on arbitrary domains. Proc. R. Soc. Lond. A 461, 2121–2133.Google Scholar
Spector, A. A., Deo, N., Grosh, K., Ratnanather, J. T. & Raphael, R. M. 2006 Electromechanical models of the outer hair cell composite membrane. J. Memb. Biol. 209, 135–152.Google Scholar
Spence, D. A. 1983 A class of biharmonic end-strip problems arising in elasticity and Stokes flow. IMA J. Appl. Math. 30, 107–139.Google Scholar
Trogdon, S. A. & Joseph, D. D. 1982 Matched eigenfunction expansions for slow flow over a slot. J. Non-Newtonian Fluid Mech. 10, 185–213.Google Scholar
Zhi, M., Ratnanather, J. T. & Brownell, W. E. 1995 Triggering water permeability change in outer hair cells. In Abstracts of the 18th Midwinter Meeting of the Association for Research in Otolaryngology, p. 155.  http://www.aro.org/archives/1995/620.html.Google Scholar
Zhi, M., Ratnanather, J. T., Ceyhan, E., Popel, A. S. & Brownell, W. E. 2007 Hypotonic swelling of salicylate-treated cochlear outer hair cells. Hear. Res. 228, 95–104.Google Scholar