Article contents
Stratified inclined duct: direct numerical simulations
Published online by Cambridge University Press: 15 August 2023
Abstract
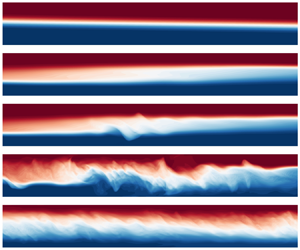
The stratified inclined duct (SID) experiment consists of a zero-net-volume exchange flow in a long tilted rectangular duct, which allows the study of realistic stratified shear flows with sustained internal forcing. We present the first three-dimensional direct numerical simulations (DNS) of SID to explore the transitions between increasingly turbulent flow regimes first described by Meyer & Linden (J. Fluid Mech., vol. 753, 2014, pp. 242–253). We develop a numerical set-up that faithfully reproduces the experiments and sustains the flow for arbitrarily long times at minimal computational cost. We recover the four qualitative flow regimes found experimentally in the same regions of parameter space: laminar flow, waves, intermittent turbulence and fully developed turbulence. We find good qualitative and quantitative agreement between DNS and experiments and highlight the added value of DNS to complement experimental diagnostics and increase our understanding of the transition to turbulence, both temporally (laminar/turbulent cycles) and parametrically (as the tilt angle of the duct and the Reynolds number are increased). These results demonstrate that numerical studies of SID – and deeper integration between simulations and experiments – have the potential to lead to a better understanding of stratified turbulence.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 7
- Cited by


