Hostname: page-component-6bb9c88b65-zjgpb Total loading time: 0 Render date: 2025-07-24T01:04:22.891Z Has data issue: false hasContentIssue false
  • English
  • Français

Streaming and diffusion in the cochlea

Published online by Cambridge University Press:  16 July 2025

Yile Li  and
Chiang C. Mei Open the ORCID record for Chiang C. Mei [Opens in a new window]
Yile Li
Affiliation:
21410 Penshore Place Ln, Katy, TX 77450, USA
Chiang C. Mei*
Affiliation:
Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
Corresponding author: Chiang C. Mei, ccmei@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

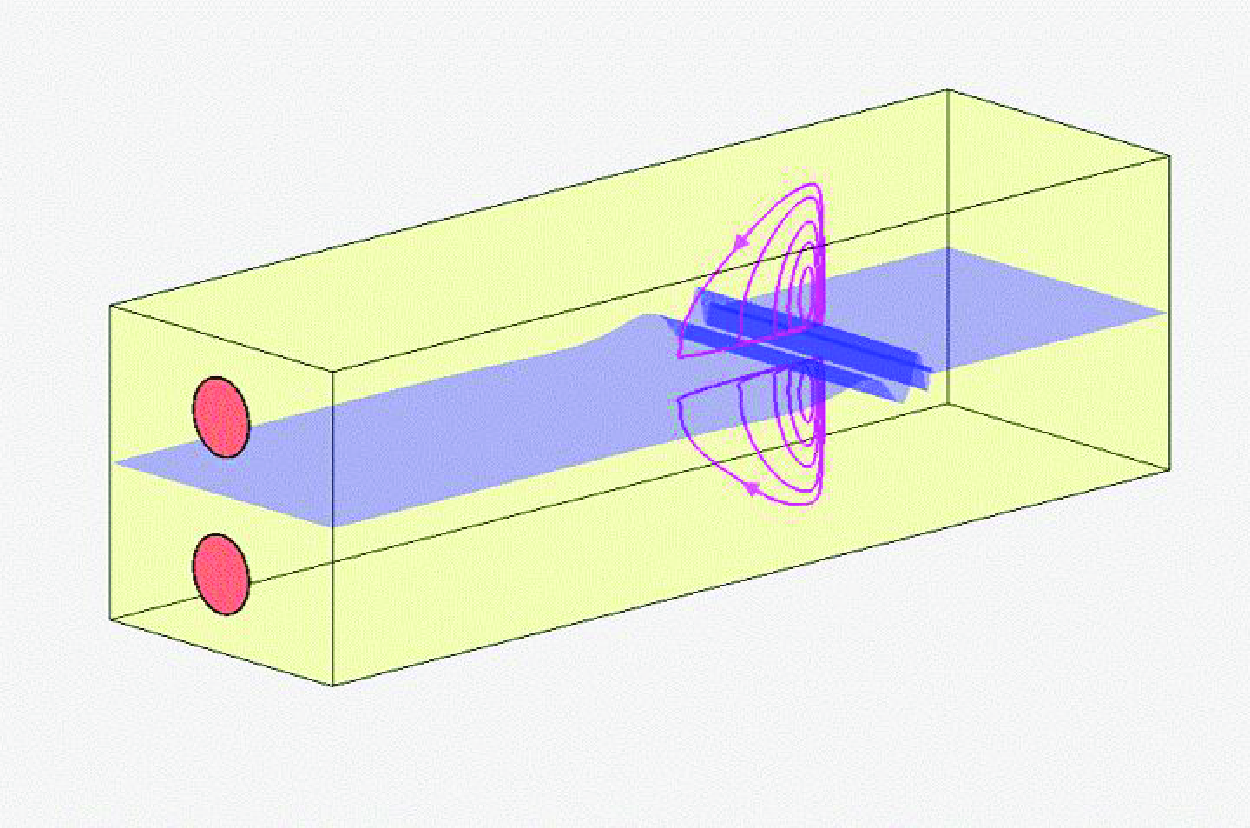
Sound entering the ear is known not only to transmit signals to the nerve system, but also to generate vortex-like steady streaming in the cochlea. This streaming has been suggested as the primary vehicle for drug delivery in the inner ear (Sumner, Mestel & Reichenbach, 2021, Sci. Rep., vol. 11, 57). An alternative vehicle by pure diffusion alone has also been suggested by Sadreev et al. (2019, Front. Cell. Neurosci., vol. 13, 161). This paper purports to examine both mechanisms analytically, and compare their relative importance, based on the two-dimensional model of Allen (1977, Acoust. Soc. Am., vol. 61, 110–119). First, we reconstruct the fluid mechanics of the Békséy vortices by an asymptotic theory of multiple scales as a complement to the two-dimensional numerical theory of Edom, Obrist & Kleiser (2014, J. Fluid Mech., vol. 753, 254–278). For discerning the difference between Sumner, Mestel & Reichenbach (2021) and Sadreev et al. (2019), we combine sound-induced streaming and molecular diffusion by modeling the drug as a solute of known diffusivity. It will be shown that due to the high frequency of sound, advection is augmented by the Lagrangian velocity, but molecular diffusion still dominates drug transport in the cochlear duct, unlike Taylor dispersion of pollutant by tides in a shallow river.

JFM classification

Biological Fluid Dynamics: Biomedical flows Biological Fluid Dynamics: Flow-vessel interactions

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1015 , 25 July 2025 , A15
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Allen, J.B. 1977 Two-dimensional cochlear fluid model: new results. J. Acoust. Soc. Am. 61 (1), 110–119.10.1121/1.381272CrossRefGoogle ScholarPubMed
Aris, A. 1960 On the dispersion of a solute in a pulsating flow through a tube. Proc. R. Soc. Lond. A 259 (1298), 370–376.Google Scholar
Batchelor, G.K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
von Békésy, G. 1960 Experiments in Hearing. McGraw-Hill.Google Scholar
de Boer, E. & MacKay, R. 1980 Reflections on reflections. J. Acoust. Soc. Am. 67 (3), 882–890.10.1121/1.383968CrossRefGoogle ScholarPubMed
Bruus, M. 2008 Theoretical Microfluidics. Oxford University Press.Google Scholar
di Cagno, M.P., Clarelli, F., Våbenø, J., Lesley, C., Rahman, S.D., Cauzzo, J., Franceschinis, E., Realdon, N. & Stein, P.C. 2018 Experimental determination of drug diffusion coefficients in unstirred aqueous environments by temporally resolved concentration measurements. Mol. Pharm. 15 (4), 1488–1494.10.1021/acs.molpharmaceut.7b01053CrossRefGoogle ScholarPubMed
Carter, T.G., Liu, P.L.F. & Mei, C.C. 1973 Mass transport by waves and offshore sand bedforms. J. Waterways, Harbours Coastal Engng Div. 99, 165–184.10.1061/AWHCAR.0000183CrossRefGoogle Scholar
Dallos, P., Popper, A.N. & Fay, R.R. 1996 The Cochlea: Springer Handbook of Auditory Research, 8, Springer-Verlag.10.1007/978-1-4612-0757-3_1CrossRefGoogle Scholar
Edom, E. 2013 Fluid flow in the cochlea, numerical investigation of steady streaming and rocking stapes motions. Doctoral thesis, ETH Zurich.Google Scholar
Edom, E., Obrist, D. & Kleiser, L. 2014 Steady streaming in a two-dimensional box model of a passive cochlea. J. Fluid Mech. 753, 254–278.10.1017/jfm.2014.360CrossRefGoogle Scholar
Eguíluz, V.M., Ospeck, M., Choe, Y., Hudspeth, A.J. & Magnasco, V.M. 2000 Essential nonlinearities in hearing. Phys. Rev. Lett. 84 (22), 5232–5235.10.1103/PhysRevLett.84.5232CrossRefGoogle ScholarPubMed
Hara, T. & Mei, C.C. 1990 Oscillating flows over periodic ripples. J. Fluid Mech. 211, 183–209.10.1017/S0022112090001549CrossRefGoogle Scholar
Hunt, J.N. & Johns, B. 1963 Currents induced by tides and gravity waves. Tellus 15 (4), 343–351.10.3402/tellusa.v15i4.8861CrossRefGoogle Scholar
Lesser, M.B. & Berkley, D.A. 1972 Fluid mechanics of the cochlea. Part 1. J. Fluid Mech. 51 (3), 497–512.10.1017/S0022112072002320CrossRefGoogle Scholar
Lien, M.D. & Cox, J.R. 1973 A mathematical model of the mechanics of the cochlea. Doctoral dissertation, Washington University, St Louis.Google Scholar
Lighthill, J. 1978 Acoustic streaming. J. Sound Vib. 61 (3), 391–418.10.1016/0022-460X(78)90388-7CrossRefGoogle Scholar
Lighthill, J. 1981 Energy flow in the cochlea. J. Fluid Mech. 106, 149–213.10.1017/S0022112081001560CrossRefGoogle Scholar
Lighthill, J. 1992 Acoustic streaming in the ear itself. J. Fluid Mech. 239, 551–606.10.1017/S0022112092004531CrossRefGoogle Scholar
Longuet-Higgins, M.S. 1953 Mass transport in water waves. Phil. Trans. R. Soc. Lond. A 245, 535–581.Google Scholar
Neely, S. 1978 Mathematical models of the mechanics of the cochlea. PhD thesis, California Institute of Technology.Google Scholar
Obrist, D. 2019 Flow phenomena in the inner ear. Ann. Rev. Fluid Mech. 51 (1), 487–510.10.1146/annurev-fluid-010518-040454CrossRefGoogle Scholar
Patel, J., Szczupak, M., Rajguru, S., Balaban, C. & Hoffer, M.E. 2019 Inner ear therapeutics: an overview of middle ear delivery. Front. Cell. Neurosci. 13 (261), 1–8.10.3389/fncel.2019.00261CrossRefGoogle ScholarPubMed
Peterson, L.C. & Bogert, B.P. 1950 A dynamical theory of the cochlea. J. Acoust. Soc. Am. 22 (3), 369–381.10.1121/1.1906615CrossRefGoogle Scholar
Rayleigh, Lord 1884 On the circulations of air observed in Kundt’s tubes and some allied acoustical problems. Phil. Mag. 175, 1–21.Google Scholar
Reichenbach, T. & Hudspeth, A.J. 2014 The physics of hearing: fluid mechanics and the active process of the inner ear. Rep. Prog. Phys. 77 (7), 243–295.10.1088/0034-4885/77/7/076601CrossRefGoogle ScholarPubMed
Riley, N. 1965 Oscillating viscous flows. Mathematika 12, 161–175.10.1112/S0025579300005283CrossRefGoogle Scholar
Sadreev, I.I., Burwood, G.W.S., Flaherty, S.L.M., Kim, J., Russell, I.J., Abdullin, T.I. & Lukashkin, A.N. 2019 Drug diffusion along an intact mammalian cochlea. Front. Cell. Neurosci. 13, 161.10.3389/fncel.2019.00161CrossRefGoogle ScholarPubMed
Schlichting, H. 1960 Boundary Layer Theory. McGraw-Hill.Google Scholar
Siebert, W.A. 1974 Rankine revisited - a simple short-wave cochlea model. J. Acoust. Soc. Am. 56, 148–162.10.1121/1.1903296CrossRefGoogle Scholar
Sim, J.H., Chatzimichalis, M., Lauxmann, M., Röösli, C., Eiber, A. & Huber, A.M. 2010 Complex stapes motions in human ears. J. Assoc. Res. Otolaryngol. 11 (3), 329–341.10.1007/s10162-010-0207-6CrossRefGoogle ScholarPubMed
Steele, C.R. & Miller, C.E. 1980 An improved WKB calculation for a two-dimensional cochlear model. J. Acoust. Soc. Am. 68 (1), 147–148.10.1121/1.384640CrossRefGoogle ScholarPubMed
Steele, C.R. & Taber, L.A. 1979 Comparison of WKB and finite difference calculations for a two-dimensional cochlear model. J. Acoust. Soc. Am. 65 (4), 1001–1006.10.1121/1.382569CrossRefGoogle ScholarPubMed
Stuart, J.T. 1966 Double boundary layers in oscillatory viscous flow. J. Fluid Mech. 24 (4), 673–687.10.1017/S0022112066000910CrossRefGoogle Scholar
Sumner, L., Mestel, J. & Reichenbach, T. 2021 Steady streaming as a method of drug delivery to the inner ear. Sci. Rep. 11 (1), 57.10.1038/s41598-020-79946-zCrossRefGoogle ScholarPubMed
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Tonndorf, J. 1970 Nonlinearities in cochlea hydrodynamics. J. Acoust. Soc. Am. 47 (2B), 579–591.10.1121/1.1911933CrossRefGoogle ScholarPubMed
Trefethen, L.N. 2000 Spectral Methods in MATLAB. SIAM.10.1137/1.9780898719598CrossRefGoogle Scholar
Vanneste, J. & Bühler, O. 2011 Streaming by leaky surface acoustic waves. Proc. R. Soc. A 467 (2130), 1779–1800.10.1098/rspa.2010.0457CrossRefGoogle Scholar
Wang, D.M. & Tarbell, J.M. 1992 Nonlinear analysis of flow in an elastic tube (artery): steady streaming effects. J. Fluid Mech. 239, 341–358.10.1017/S0022112092004439CrossRefGoogle Scholar
Zweig, G., Lipes, R. & Pierce, J.R. 1976 The cochlea compromise. J. Acoust. Soc. Am. 59 (4), 975–982.10.1121/1.380956CrossRefGoogle ScholarPubMed