Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T17:23:34.029Z Has data issue: false hasContentIssue false
  • English
  • Français

Streaming-potential phenomena in the thin-Debye-layer limit. Part 2. Moderate Péclet numbers

Published online by Cambridge University Press:  03 July 2012

Ory Schnitzer ,
Itzchak Frankel  and
Ehud Yariv
Ory Schnitzer
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
Itzchak Frankel
Affiliation:
Department of Aerospace Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: udi@technion.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

Macroscale description of streaming-potential phenomena in the thin-double-layer limit, and in particular the associated electro-viscous forces, has been a matter of long-standing controversy. In part 1 of this work (Yariv, Schnitzer & Frankel, J. Fluid Mech., vol. 685, 2011, pp. 306–334) we identified that the product of the Hartmann (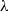) and Péclet (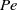) numbers is 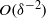, 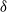being the dimensionless Debye thickness. This scaling relationship defines a one-family class of limit processes appropriate to the consistent analysis of this singular problem. In that earlier contribution we focused on the generic problems associated with moderate 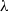and large 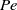, where the streaming-potential magnitude is comparable to the thermal voltage. Here we consider the companion generic limit of moderate Péclet numbers and large Hartmann numbers, deriving the appropriate macroscale model wherein the Debye-layer physics is represented by effective boundary conditions. Since the induced electric field is asymptotically smaller, calculation of these conditions requires higher asymptotic orders in analysing the Debye-scale transport. Nonetheless, the leading-order electro-viscous forces are of the same 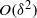relative magnitude as those previously obtained in the large- 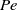limit. The structure of these forces is different, however, first because the small Maxwell stresses do not contribute at leading order, and second because salt polarization results in a dominant diffuso-osmotic slip. Since the salt distribution is governed by an advection–diffusion equation, this slip gives rise to electro-viscous forces which are nonlinear in the driving flow. The resulting scheme is illustrated by the calculation of the electro-viscous excess drag in the prototype problem of a translating sphere.

JFM classification

Complex Fluids: Colloids Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 704 , 10 August 2012 , pp. 109 - 136
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alexander, B. M. & Prieve, D. C. 1987 A hydrodynamic technique for measurement of colloidal forces. Langmuir 3 (5), 788–795.CrossRefGoogle Scholar
2. Bike, S. G. & Prieve, D. C. 1990 Electrohydrodynamic lubrication with thin double layers. J. Colloid Interface Sci. 136 (1), 95–112.CrossRefGoogle Scholar
3. Bike, S. G. & Prieve, D. C. 1992 Electrohydrodynamics of thin double layers: a model for the streaming potential profile. J. Colloid Interface Sci. 154, 87–96.CrossRefGoogle Scholar
4. Booth, F. 1950 The cataphoresis of spherical, solid non-conducting particles in a symmetrical electrolyte. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 203 (1075), 514.Google Scholar
5. Booth, F. 1954 Sedimentation potential and velocity of solid spherical particles. J. Chem. Phys. 22, 1956–1968.CrossRefGoogle Scholar
6. Brenner, H. 1964 The Stokes resistance of an arbitrary particle. Part 4. Arbitrary fields of flow. Chem. Engng Sci. 19, 703–727.CrossRefGoogle Scholar
7. Cox, R. G. 1997 Electroviscous forces on a charged particle suspended in a flowing liquid. J. Fluid Mech. 338, 1–34.CrossRefGoogle Scholar
8. Dukhin, S. S. 1993 Non-equilibrium electric surface phenomena. Adv. Colloid Interface Sci. 44, 1–134.CrossRefGoogle Scholar
9. Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Prentice-Hall.Google Scholar
10. Keh, H. J. & Anderson, J. L. 1985 Boundary effects on electrophoretic motion of colloidal spheres. J. Fluid Mech. 153, 417–439.CrossRefGoogle Scholar
11. Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.CrossRefGoogle Scholar
12. Michelin, S. & Lauga, E. 2011 Optimal feeding is optimal swimming for all Péclet numbers. Phys. Fluids 23, 101901.CrossRefGoogle Scholar
13. Morrison, F. A. 1970 Electrophoresis of a particle of arbitrary shape. J. Colloid Interface Sci. 34, 210–214.CrossRefGoogle Scholar
14. O’Brien, R. W. & White, L. R. 1978 Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc. Faraday Trans. 2 (74), 1607–1626.CrossRefGoogle Scholar
15. Ohshima, H., Healy, T. W., White, L. R. & O’Brien, R. W. 1984 Sedimentation velocity and potential in a dilute suspension of charged spherical colloidal particles. J. Chem. Soc. Faraday Trans. 80 (10), 1299–1317.CrossRefGoogle Scholar
16. Overbeek, J. T. G. 1943 Theorie der Elektrophorese: der Relaxationseffekt. Kolloid-Beihefte 54, 287.CrossRefGoogle Scholar
17. Prieve, D. C., Ebel, J. P., Anderson, J. L. & Lowell, M. E. 1984 Motion of a particle generated by chemical gradients. Part 2. Electrolytes. J. Fluid Mech. 148, 247–269.CrossRefGoogle Scholar
18. Rubinstein, I. & Zaltzman, B. 2001 Electro-osmotic slip of the second kind and instability in concentration polarization at electrodialysis membranes. Math. Models Meth. Appl. Sci. 11, 263–300.CrossRefGoogle Scholar
19. Saville, D. A. 1977 Electrokinetic effects with small particles. Annu. Rev. Fluid Mech. 9, 321–337.CrossRefGoogle Scholar
20. Schnitzer, O., Khair, A. & Yariv, E. 2011 Irreversible electrokinetic repulsion in zero-Reynolds-number sedimentation. Phys. Rev. Lett. 107, 278301.CrossRefGoogle ScholarPubMed
21. Smoluchowski, M. 1921 Elektrische Endosmose und Strömungsströme. In Handbuch der Elektrizität und des Magnetismus, vol. II, Stationäre Ströme (ed. Graetz, L. ). Barth.Google Scholar
22. Tabatabaei, S. M., van de Ven, T. G. M. & Rey, A. D. 2006 Electroviscous sphere-wall interactions. J. Colloid Interface Sci. 301 (1), 291–301.CrossRefGoogle ScholarPubMed
23. Van Dyke, M. 1964 Perturbation Methods in Fluid Mechanics. Academic.Google Scholar
24. van de Ven, T. G. M., Warszynski, P. & Dukhin, S. S. 1993 Electrokinetic lift of small particles. J. Colloid Interface Sci. 157 (2), 328–331.CrossRefGoogle Scholar
25. Warszyski, P., Wu, X. & van de Ven, T. 1998 Electrokinetic lift force for a charged particle moving near a charged wall: a modified theory and experiment. Colloid Surf. A 140 (1-3), 183–198.CrossRefGoogle Scholar
26. Yariv, E. 2006 Force-free electrophoresis? Phys. Fluids 18, 031702.CrossRefGoogle Scholar
27. Yariv, E. 2010 An asymptotic derivation of the thin-Debye-layer limit for electrokinetic phenomena. Chem. Engng Commun. 197, 3–17.CrossRefGoogle Scholar
28. Yariv, E. & Davis, A. 2010 Electro-osmotic flows over highly polarizable dielectric surfaces. Phys. Fluids 22, 052006.CrossRefGoogle Scholar
29. Yariv, E., Schnitzer, O. & Frankel, I. 2011 Streaming-potential phenomena in the thin-Debye-layer limit. Part 1. General theory. J. Fluid Mech. 685, 306–334.CrossRefGoogle Scholar
30. Yossifon, G., Frankel, I. & Miloh, T. 2007 Symmetry breaking in induced-charge electro-osmosis over polarizable spheroids. Phys. Fluids 19, 068105.CrossRefGoogle Scholar