1. Introduction
For certain problems in turbulent flows, there are advantages in representing the flow equations in coordinates that approximate the flow streamlines and various analyses that use such approaches have appeared in the literature. At a practical level, if one coordinate direction can be chosen almost parallel to the mean flow direction, then extra terms arising from deviations of the mean flow from the coordinates may be small enough to be approximated or ignored in calculation schemes. A second advantage is that, in thin shear layers and boundary layers, the maximum strain applied to the flow is shear at right angles to the mean flow direction so that the response of turbulent stresses to this straining can be calculated most simply in an approximately streamline coordinate frame. In non-separating flows close to solid surfaces, surface-following coordinates form a reasonable approximation to the streamlines and Howarth (Reference Howarth1951) developed the surface-normal or s-n coordinate system for use in analysing three-dimensional (3-D) boundary layer flows. Howarth's s-n system consists of a family of Lame surfaces, parallel to the solid surface, together with two families of orthogonal surfaces forming a normal congruence with the Lame surfaces. The intersections of these three families of surfaces furnish the coordinate lines. An equivalent 2-D s-n system was developed independently by Janour (Reference Janour1975). Bradshaw (Reference Bradshaw1973) showed that the s-n system was also appropriate for use in thin shear layers and he applied it in his analysis of curved shear flows. However, although surface-following coordinates approximate streamlines very close to a solid surface, as we move away from the surface the streamlines will tend to become parallel, as we see for example in flow around an aerofoil outside the boundary layer or in atmospheric flow above hilly topography, so that s-n coordinates are then as inappropriate as Cartesian coordinates are close to the surface.
As a result, true streamline coordinates have remained an attractive goal for computation and analysis of complex shear flows. When the situation being modelled is straining of turbulence by a distorted irrotational mean flow, the mean streamlines can be computed to first order by potential flow theory, as in Hunt (Reference Hunt1973) or Durbin & Hunt (Reference Durbin and Hunt1980). When the flow is being modelled by methods of computational fluid dynamics such as higher-order turbulence closures or large eddy simulations, orthogonal coordinates appropriate for 2-D flows have been generated by using von Mises transform (Barron Reference Barron1989). The study of Zeman & Jensen (Reference Zeman and Jensen1987) is particularly relevant here as they used that approach to transform a second-order closure model of atmospheric boundary layer flow into streamline coordinates, obtaining first and second moment equations identical to those derived using more general tensor methods by Finnigan (Reference Finnigan1983) (henceforth F83). By comparing their numerical solutions with field measurements over a 2-D ridge, they were able to show the important role played by streamline curvature in modulating turbulent stresses over the hill. In more complex 3-D flows, non-orthogonal streamline coordinates have also been used to optimise calculations, for example by Sullivan, McWilliams & Patton (Reference Sullivan, McWilliams and Patton2014), who used a non-orthogonal streamline system to compute flow over water waves.
The immediate motivation for the present work has been the computation of atmospheric flows over hilly topography or the interpretation of measurements made in such flows. For roughly two decades, beginning around 1970, studies of flow over hills was one of the main fields of interest in boundary layer meteorology and its development has recently been reviewed in detail by Finnigan et al. (Reference Finnigan, Ayotte, Harman, Katul, Oldroyd, Patton, Poggi, Ross and Taylor2020). Our conceptual understanding of such flows was greatly influenced by the analytic theory of Jackson & Hunt (Reference Jackson and Hunt1975) (henceforth JH75) and the series of studies that followed it. JH75 developed a model for neutrally stratified flow over a low rough hill by linearising the equations of motion for the hill-induced flow perturbations about a background wind profile. Their key insight was that the flow can be divided into two layers: a thin inner layer near the surface, where perturbations to the turbulent Reynolds stress terms are important, and an outer layer, where the flow perturbations are essentially an inviscid response to the pressure field that develops around the hill. Scaling analysis yields different leading-order terms and to a separate analytical solution in each layer. These were then matched asymptotically to give an overall solution. Further refinements to this approach (discussed in Finnigan et al. Reference Finnigan, Ayotte, Harman, Katul, Oldroyd, Patton, Poggi, Ross and Taylor2020), particularly a rigorous analysis of the matching process by Sykes (Reference Sykes1980), led eventually to a major paper by Hunt, Leibovich & Richards (Reference Hunt, Leibovich and Richards1988), where the two layers were each divided into sublayers so that surface and outer boundary conditions could be formally satisfied. An in-depth review by Finnigan (Reference Finnigan, Steffen and Denmead1988) summarised the state of theory and experimental results on boundary layer flow over hills up to that date and described in detail the advances in understanding to be gained when experimental data over 2-D hills are analysed in streamline coordinates.
As discussed in some detail by Van Dyke (Reference Van Dyke1975), choice of coordinate systems can be critical when applying the method of matched asymptotic expansions to small-perturbation solutions of problems in fluid dynamics. In JH75 and Hunt et al. (Reference Hunt, Leibovich and Richards1988), the outer layer solutions were obtained in Cartesian coordinates while the inner layer equations were developed in surface-following coordinates. While not affecting the conceptual basis of their results, the mismatch of coordinates did influence the numerical accuracy of the model and is particularly important when the perturbation solutions are expanded to second order, as is necessary to compute changes to the pressure field that follow the first-order changes to the velocity field. Hence, in later developments of the theory, Belcher (Reference Belcher1990) and Belcher, Newley & Hunt (Reference Belcher, Newley and Hunt1993) adopted a coordinate system consisting of the streamfunction and potential function of inviscid irrotational flow over a 2-D hill. This approach was equivalent to the von Mises transform of Zeman & Jensen (Reference Zeman and Jensen1987), noted above. However, while this furnished them with a coordinate system that followed the surface exactly but relaxed to parallel flow aloft, they did not transform the dependent variables in their equations, the velocity components remaining in Cartesian coordinates.
Developing this asymptotic expansion approach further, Finnigan & Belcher (Reference Finnigan and Belcher2004) produced an analytic model of flow over a 2-D ridge covered with a tall plant canopy. Their model followed the overall structure of Hunt et al. (Reference Hunt, Leibovich and Richards1988) but replaced Hunt et al.'s inner surface layer with a two-layer canopy representation, comprising a linearised upper canopy and a nonlinear lower canopy formulation. Their model was able to show why flow separation and increased form drag on topography occurred at much lower angles on hills covered with canopies than on rough hills of the same geometry. They also adopted a coordinate system composed of the streamfunction and potential function of inviscid flow but took the further step of using the streamline coordinate theory of F83 to transform both the coordinates and the dependent variables in the flow equations, leading to more intuitive perturbation expansions and matching of inner and outer layer solutions.
While the basic theory of JH75 and later Hunt et al. (Reference Hunt, Leibovich and Richards1988) was equally applicable to 2-D or 3-D hills and the studies of Mason & Sykes (Reference Mason P and Sykes1979) and Sykes (Reference Sykes1980) specifically dealt with 3-D isolated hills, they all suffered from the problem of a mismatch between a Cartesian representation of the outer flow and the use of surface-following coordinates for the inner layer. Although inviscid flow solutions over 3-D topography can be obtained by numerical or approximate methods and so can generate a driving pressure field, there exists no accompanying 3-D streamline theory able to generate coordinates that smoothly change from surface following to Cartesian with distance from the surface. Similarly, the further step of deriving the perturbation equations from a rational scale analysis, of the transformed flow equations, as Finnigan & Belcher (Reference Finnigan and Belcher2004) were able to do using the 2-D theory of F83, is unavailable for general topography. As a result, there has been continuing interest in finding equivalent coordinate systems for general 3-D flow fields.
The second main application of streamline coordinate representations is in the interpretation of measurements in complex boundary layer flows. When the mean streamlines of a curved flow make a significant angle with a Cartesian reference frame, interpretation of the evolution of the turbulent stresses and their relationship to the mean strain field is at best non-intuitive and at worst almost impossible. The review by Finnigan (Reference Finnigan, Steffen and Denmead1988) mentioned above showed how transformation of the equations for the first and second moments of the turbulent flow into the 2-D streamline coordinate system of F83 allowed the flow dynamics of both wind tunnel simulations and field experiments to be interpreted by straightforward extensions of methods familiar from plane boundary layer flows. It was for the same reason that Zeman & Jensen (Reference Zeman and Jensen1987) transformed a second-order closure model, originally designed for horizontally homogeneous planetary boundary layers, into streamline coordinates to interpret field measurements made over a 2-D ridge.
In many cases, however, field measurements of turbulent fluxes, for example, those made on the several hundreds of ‘flux towers’ deployed in the global FLUXNET experiment (fluxnet.org), or when arrays of flux towers are deployed to measure atmospheric flow over complex topography, for example as in the international Perdigao field campaign, discussed with many other examples in Finnigan et al. (Reference Finnigan, Ayotte, Harman, Katul, Oldroyd, Patton, Poggi, Ross and Taylor2020), it is impossible to relate the measurements to any notional objective Cartesian frame. Instead, velocity components obtained in the reference frame of the sonic anemometer are rotated post facto into a local Cartesian frame whose ‘x axis’ is parallel to the mean velocity vector. Since only the direction of the x axis can be defined unambiguously from mean velocity components measured by the anemometer, extra information has to be supplied to fix the directions of the y and z axes. Two methods are in most common use. The first employs the components of the mean wind vector and the Reynolds stress tensor to define those directions, while the ‘planar-fit’ method (Wilczak, Oncley & Stage Reference Wilczak, Oncley and Stage2001) uses instead an ensemble of mean wind vectors obtained at different times. The two methods are compared and their relationship to 3-D streamline coordinates described in Finnigan (Reference Finnigan2004). Whichever method is used, the experimentalist is left with the task of relating measurements of mean velocities and turbulent stresses made in spatially varying coordinate systems. If the objective is (as it usually is) to construct scalar or momentum budgets in some relevant control volume, then the budget must be constructed in a streamline coordinate frame as the separated measurements are automatically aligned with that frame. When the flow is close to two-dimensional, then this can be done in the F83 2-D coordinate system, but in more complex situations, a 3-D streamline system is needed.
With these motivations, the goal of this paper is to investigate how we can extend the 2-D streamline coordinate theory of F83 to 3-D turbulent flows so, in the following § 2, as a starting point for the full 3-D development that follows, we briefly review the essential characteristics of the 2-D theory.
2. Flow equations in two-dimensional Streamline coordinates
2.1. Notation
Many of the formulae in this paper can be derived most directly using the modern description of curves on manifolds, which exploits the correspondence between a vector basis and the dual basis of one-forms, see for example, Misner, Thorne & Wheeler (Reference Misner, Thorne and Wheeler1970) or Schutz (Reference Schutz1980). However, this approach is probably unfamiliar to many readers and so results are presented in more familiar tensor notation except in Appendix B, where the use of the dual basis avoids tedious index gymnastics. Elsewhere, vectors and tensors are denoted by bold letters and their components by lower case letters. Base vectors are distinguished by lower indices, e.g. ![]() ${\boldsymbol{e}_i}$, where the index i denotes the base vector not the component. Components of vectors and tensors are distinguished by upper indices so that a vector
${\boldsymbol{e}_i}$, where the index i denotes the base vector not the component. Components of vectors and tensors are distinguished by upper indices so that a vector ![]() $\boldsymbol{a}$ can be written,
$\boldsymbol{a}$ can be written, ![]() $\boldsymbol{a} = {a^1}{\boldsymbol{e}_1} + {a^2}{\boldsymbol{e}_2} + {a^3}{\boldsymbol{e}_3}$. We have adopted the mathematical convention of treating directional derivatives as vectors, hence the base vector
$\boldsymbol{a} = {a^1}{\boldsymbol{e}_1} + {a^2}{\boldsymbol{e}_2} + {a^3}{\boldsymbol{e}_3}$. We have adopted the mathematical convention of treating directional derivatives as vectors, hence the base vector ![]() ${\boldsymbol{e}_i}$ can also be written as the directional derivative along a space curve
${\boldsymbol{e}_i}$ can also be written as the directional derivative along a space curve ![]() ${x^i}$ so that
${x^i}$ so that ![]() ${\boldsymbol{e}_i} = \textrm{d}/\textrm{d}\kern0.07em{x^i} = {\partial _i}$ and the components of
${\boldsymbol{e}_i} = \textrm{d}/\textrm{d}\kern0.07em{x^i} = {\partial _i}$ and the components of ![]() ${\boldsymbol{e}_i}$ at a point P, whose coordinates in the background Cartesian reference coordinate frame are
${\boldsymbol{e}_i}$ at a point P, whose coordinates in the background Cartesian reference coordinate frame are ![]() $P({\kern0.9pt}\boldsymbol{y}) = \{ {y^1},{y^2},{y^3}\} $ become
$P({\kern0.9pt}\boldsymbol{y}) = \{ {y^1},{y^2},{y^3}\} $ become ![]() $\textrm{d}\boldsymbol{y}/\textrm{d}\kern0.07em{x^i} = {\partial _i}\boldsymbol{y}$. Other variables are defined as encountered in the text.
$\textrm{d}\boldsymbol{y}/\textrm{d}\kern0.07em{x^i} = {\partial _i}\boldsymbol{y}$. Other variables are defined as encountered in the text.
2.2. Two-dimensional momentum equations
The streamline coordinate system for 2-D shear flows developed in F83 employs the Lagrange streamfunction ![]() $\psi ({\kern0.9pt}\boldsymbol{y})$ and a modified potential function
$\psi ({\kern0.9pt}\boldsymbol{y})$ and a modified potential function ![]() $\phi ({\kern0.9pt}\boldsymbol{y})$ as the
$\phi ({\kern0.9pt}\boldsymbol{y})$ as the ![]() ${x^2}$ and
${x^2}$ and ![]() ${x^1}$ coordinates, respectively, where
${x^1}$ coordinates, respectively, where ![]() $\boldsymbol{y} = \{ {y^1},{y^2},{y^3}\} $ is the background reference rectangular Cartesian coordinate frame. For axisymmetric shear flows, the Lagrange streamfunction is replaced by the Stokes streamfunction (Finnigan Reference Finnigan1990). Vector and tensor flow variables are referred to an orthogonal basis consisting of the tangent vectors to the coordinate lines. The coordinate lines in turn are given by the intersections of constant surfaces of the streamfunction, the modified potential function and the planes of symmetry. Written in this true coordinate system, the flow equations contain familiar partial derivatives but distance along the
$\boldsymbol{y} = \{ {y^1},{y^2},{y^3}\} $ is the background reference rectangular Cartesian coordinate frame. For axisymmetric shear flows, the Lagrange streamfunction is replaced by the Stokes streamfunction (Finnigan Reference Finnigan1990). Vector and tensor flow variables are referred to an orthogonal basis consisting of the tangent vectors to the coordinate lines. The coordinate lines in turn are given by the intersections of constant surfaces of the streamfunction, the modified potential function and the planes of symmetry. Written in this true coordinate system, the flow equations contain familiar partial derivatives but distance along the ![]() ${x^1}$ and
${x^1}$ and ![]() ${x^2}$ coordinate lines is measured in units of
${x^2}$ coordinate lines is measured in units of ![]() $\phi $ and
$\phi $ and ![]() $\psi $, respectively. As a result, physical quantities acquire unfamiliar dimensions. For example, the transformed velocity vector
$\psi $, respectively. As a result, physical quantities acquire unfamiliar dimensions. For example, the transformed velocity vector ![]() $\boldsymbol{u}$ has dimensions
$\boldsymbol{u}$ has dimensions ![]() ${L^2}/{T^2}$ rather than
${L^2}/{T^2}$ rather than ![]() $L/T$. F83, therefore, took the further step of normalising this vector basis to an orthonormal basis and parameterising the coordinate lines by physical distance so that flow variables appearing in the equations take their familiar dimensions. The trade-off for this transform to physical coordinates (Truesdell Reference Truesdell1953; Aris Reference Aris1962) is that partial derivatives are replaced by directional derivatives. These ‘physical streamline coordinate equations’ are suitable for interpreting measurements or forming a basis for small-perturbation theories of flow over hills, as discussed earlier. In this sense physical equations differ from transforms from Cartesian to true curvilinear coordinates, which are intended to simplify calculations, for example by making the governing equations separable, and where partial derivatives are retained. The most fundamental difference between streamline coordinates and conventional coordinate systems, however, is that the coordinate frame is determined by the flow field itself rather than being externally prescribed.
$L/T$. F83, therefore, took the further step of normalising this vector basis to an orthonormal basis and parameterising the coordinate lines by physical distance so that flow variables appearing in the equations take their familiar dimensions. The trade-off for this transform to physical coordinates (Truesdell Reference Truesdell1953; Aris Reference Aris1962) is that partial derivatives are replaced by directional derivatives. These ‘physical streamline coordinate equations’ are suitable for interpreting measurements or forming a basis for small-perturbation theories of flow over hills, as discussed earlier. In this sense physical equations differ from transforms from Cartesian to true curvilinear coordinates, which are intended to simplify calculations, for example by making the governing equations separable, and where partial derivatives are retained. The most fundamental difference between streamline coordinates and conventional coordinate systems, however, is that the coordinate frame is determined by the flow field itself rather than being externally prescribed.
The streamwise and cross-stream momentum equations for steady, incompressible, neutrally stratified, 2-D turbulent flow in this system become, respectively,
 \begin{align}U{\partial _1}U =
\dfrac{{{U^2}}}{{{L_a}}} &={-} {\partial _1}P - {\partial
_1}\overline {{u^1}{u^1}} - {\partial _2}\overline
{{u^1}{u^2}} + \dfrac{1}{{{L_a}}}(\overline {{u^1}{u^1}} -
\overline {{u^2}{u^2}} ) + \dfrac{{2\overline {{u^1}{u^2}}
}}{R}\nonumber\\ & \quad + \nu \left[
{{\partial_1}({\partial_1}U) + {\partial_2}({\partial_2}U)
- \dfrac{2}{{{L_a}}}{\partial_1}U -
\dfrac{1}{R}{\partial_2}U - \dfrac{U}{{{R^2}}}}
\right],
\end{align}
\begin{align}U{\partial _1}U =
\dfrac{{{U^2}}}{{{L_a}}} &={-} {\partial _1}P - {\partial
_1}\overline {{u^1}{u^1}} - {\partial _2}\overline
{{u^1}{u^2}} + \dfrac{1}{{{L_a}}}(\overline {{u^1}{u^1}} -
\overline {{u^2}{u^2}} ) + \dfrac{{2\overline {{u^1}{u^2}}
}}{R}\nonumber\\ & \quad + \nu \left[
{{\partial_1}({\partial_1}U) + {\partial_2}({\partial_2}U)
- \dfrac{2}{{{L_a}}}{\partial_1}U -
\dfrac{1}{R}{\partial_2}U - \dfrac{U}{{{R^2}}}}
\right],
\end{align} \begin{align}\dfrac{{{U^2}}}{R} &={-} {\partial _2}P - {\partial _1}\overline {{u^1}{u^2}} - {\partial _2}\overline {{u^2}{u^2}} + (\overline {{u^1}{u^1}} - \overline {{u^2}{u^2}} )\dfrac{1}{R} + 2\dfrac{{\overline {{u^1}{u^2}} }}{{{L_a}}}\nonumber\\ & \quad - \nu \left[ {{\partial_1}({\partial_2}U) - \dfrac{1}{{{L_a}}}{\partial_2}U - {\partial_1}\left( {\dfrac{U}{R}} \right) - \dfrac{U}{{R{L_a}}}} \right]. \end{align}
\begin{align}\dfrac{{{U^2}}}{R} &={-} {\partial _2}P - {\partial _1}\overline {{u^1}{u^2}} - {\partial _2}\overline {{u^2}{u^2}} + (\overline {{u^1}{u^1}} - \overline {{u^2}{u^2}} )\dfrac{1}{R} + 2\dfrac{{\overline {{u^1}{u^2}} }}{{{L_a}}}\nonumber\\ & \quad - \nu \left[ {{\partial_1}({\partial_2}U) - \dfrac{1}{{{L_a}}}{\partial_2}U - {\partial_1}\left( {\dfrac{U}{R}} \right) - \dfrac{U}{{R{L_a}}}} \right]. \end{align} In (2.1) and (2.2), ![]() ${\partial _i}$ denotes a directional derivative in the
${\partial _i}$ denotes a directional derivative in the ![]() ${x^i}$ coordinate direction. The
${x^i}$ coordinate direction. The ![]() ${x^1}$ coordinate lines are the streamlines while the
${x^1}$ coordinate lines are the streamlines while the ![]() ${x^2}$ coordinates are the orthogonal trajectories to the streamlines. The
${x^2}$ coordinates are the orthogonal trajectories to the streamlines. The ![]() ${x^3}$ coordinates are the straight lines normal to the planes of symmetry
${x^3}$ coordinates are the straight lines normal to the planes of symmetry ![]() ${y^3} = \textrm{constant}$ (figure 1). Here U is the mean velocity,
${y^3} = \textrm{constant}$ (figure 1). Here U is the mean velocity, ![]() ${u^i}$ is the turbulent velocity fluctuation in the
${u^i}$ is the turbulent velocity fluctuation in the ![]() ${x^i}$ direction, P is the mean kinematic pressure and
${x^i}$ direction, P is the mean kinematic pressure and ![]() $\nu $ is the kinematic viscosity. The overbar denotes an ensemble or time average. Since the flow is two-dimensional, there are no terms involving
$\nu $ is the kinematic viscosity. The overbar denotes an ensemble or time average. Since the flow is two-dimensional, there are no terms involving ![]() ${\partial _3}$ or
${\partial _3}$ or ![]() ${u^3}$. Two parameters representing flow geometry appear in the equations. Here R is the local radius of curvature of the streamlines and is related to
${u^3}$. Two parameters representing flow geometry appear in the equations. Here R is the local radius of curvature of the streamlines and is related to ![]() ${\varOmega ^3}$, the
${\varOmega ^3}$, the ![]() ${x^3}$ component of the mean vorticity, which in this coordinate system takes the form,
${x^3}$ component of the mean vorticity, which in this coordinate system takes the form, ![]() ${\varOmega ^3} = (U/R - {\partial _2}U)$;
${\varOmega ^3} = (U/R - {\partial _2}U)$; ![]() ${L_a}$ is the e-folding distance of streamwise acceleration and is also the local radius of curvature of the
${L_a}$ is the e-folding distance of streamwise acceleration and is also the local radius of curvature of the ![]() ${x^2}$ coordinate lines;
${x^2}$ coordinate lines; ![]() ${L_a}$ is related to the continuity equation for this solenoidal flow as the expression
${L_a}$ is related to the continuity equation for this solenoidal flow as the expression ![]() $\boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{u} = 0$ transforms to
$\boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{u} = 0$ transforms to ![]() ${\partial _1}U - U/{L_a} = 0$ so that
${\partial _1}U - U/{L_a} = 0$ so that ![]() $1/{L_a} = ({\partial _1}U)/U$. Through these parameters, the response of the turbulent stresses to flow acceleration and curvature becomes transparent. A further interesting property of these equations is that (2.1) contains all the information about changes in the linear momentum of the flow
$1/{L_a} = ({\partial _1}U)/U$. Through these parameters, the response of the turbulent stresses to flow acceleration and curvature becomes transparent. A further interesting property of these equations is that (2.1) contains all the information about changes in the linear momentum of the flow ![]() $U{\partial _1}U$, which are always directed along the tangent to the streamline, and (2.2) contains all the information about the angular momentum of the flow
$U{\partial _1}U$, which are always directed along the tangent to the streamline, and (2.2) contains all the information about the angular momentum of the flow ![]() ${U^2}/R$, which is always directed along the principal normal to the streamline, the direction in which the streamline has its maximum curvature.
${U^2}/R$, which is always directed along the principal normal to the streamline, the direction in which the streamline has its maximum curvature.

Figure 1. Coordinate surfaces and base vectors in the 2-D streamline coordinate system.
In addition to the turbulence terms, which require closure assumptions to represent them as functions of the mean flow, (2.1) and (2.2) have three unknowns, U, ![]() $1/R$ and P instead of the conventional
$1/R$ and P instead of the conventional ![]() ${U^1},\;{U^2},\;P$, which would appear in Cartesian coordinates. However, the continuity equation
${U^1},\;{U^2},\;P$, which would appear in Cartesian coordinates. However, the continuity equation ![]() $\boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{u} = 0$, which would close the equation set in Cartesian coordinates, is now incorporated into (2.1) and (2.2) through the geometric coefficient
$\boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{u} = 0$, which would close the equation set in Cartesian coordinates, is now incorporated into (2.1) and (2.2) through the geometric coefficient ![]() $(1/{L_a})$ so the equation set is closed through the structure equation (2.3), which describes the constraint on the mutual orientation of the base vectors in E3
$(1/{L_a})$ so the equation set is closed through the structure equation (2.3), which describes the constraint on the mutual orientation of the base vectors in E3
The vector basis of the physical F83 system is a right-handed orthonormal triad, ![]() $\{ {\boldsymbol{e}_1},{\boldsymbol{e}_2},{\boldsymbol{e}_3}\} $. This is a special case of the Serret–Frenet basis of a space curve. If we identify the tangent to the streamline with
$\{ {\boldsymbol{e}_1},{\boldsymbol{e}_2},{\boldsymbol{e}_3}\} $. This is a special case of the Serret–Frenet basis of a space curve. If we identify the tangent to the streamline with ![]() ${\boldsymbol{e}_1}$, its principal normal with
${\boldsymbol{e}_1}$, its principal normal with ![]() ${\boldsymbol{e}_2}$ and its binormal with
${\boldsymbol{e}_2}$ and its binormal with ![]() ${\boldsymbol{e}_3}$, the three vectors are linked by the Serret–Frenet equations (Aris Reference Aris1962)
${\boldsymbol{e}_3}$, the three vectors are linked by the Serret–Frenet equations (Aris Reference Aris1962)
where ![]() $1/R$ is the curvature and
$1/R$ is the curvature and ![]() $1/\sigma $ the torsion or twist of the streamlines. The plane spanned by
$1/\sigma $ the torsion or twist of the streamlines. The plane spanned by ![]() ${\boldsymbol{e}_1}$ and the principal normal
${\boldsymbol{e}_1}$ and the principal normal ![]() ${\boldsymbol{e}_2}$ is called the osculating plane and the maximum curvature of the streamline is given by its projection onto this plane. The plane spanned by
${\boldsymbol{e}_2}$ is called the osculating plane and the maximum curvature of the streamline is given by its projection onto this plane. The plane spanned by ![]() ${\boldsymbol{e}_1}$ and the binormal
${\boldsymbol{e}_1}$ and the binormal ![]() ${\boldsymbol{e}_3}$ is called the tangent plane and the third plane, spanned by
${\boldsymbol{e}_3}$ is called the tangent plane and the third plane, spanned by ![]() ${\boldsymbol{e}_2}$ and
${\boldsymbol{e}_2}$ and ![]() ${\boldsymbol{e}_3}$, is known as the normal plane. In the 2-D case treated in F83, the streamlines are confined to the planes of symmetry and so are plane curves with
${\boldsymbol{e}_3}$, is known as the normal plane. In the 2-D case treated in F83, the streamlines are confined to the planes of symmetry and so are plane curves with ![]() $1/\sigma = 0$. A vector basis such as
$1/\sigma = 0$. A vector basis such as ![]() ${\boldsymbol{e}_i}$, which is defined by the properties of the space curve which generates it, is known as a moving frame. We shall find it useful to distinguish a vector basis generated by rescaling a true coordinate basis, as in the physical F83 system described above, by calling it a non-coordinate basis although it is also a special case of a moving frame.
${\boldsymbol{e}_i}$, which is defined by the properties of the space curve which generates it, is known as a moving frame. We shall find it useful to distinguish a vector basis generated by rescaling a true coordinate basis, as in the physical F83 system described above, by calling it a non-coordinate basis although it is also a special case of a moving frame.
The rest of this paper addresses the question of, under what circumstances can we extend the physical coordinate representation of (2.1) and (2.2), with its desirable separation of angular and streamwise momentum and transparent influence of curvature and acceleration, to general 3-D flows, where the streamlines may be twisted curves?
The analysis is set out as follows: in § 3 we derive the general form of 3-D flow equations in the streamline Serret–Frenet basis ![]() ${\boldsymbol{e}_i}$. This focusses the question above to that of defining the way that the components of
${\boldsymbol{e}_i}$. This focusses the question above to that of defining the way that the components of ![]() ${\boldsymbol{e}_i}$ vary as we move along the streamline
${\boldsymbol{e}_i}$ vary as we move along the streamline ![]() ${x^1}$ and its orthogonal trajectories,
${x^1}$ and its orthogonal trajectories, ![]() ${x^2}$ and
${x^2}$ and ![]() ${x^3}$, which we wish to use as coordinate lines. We then show in § 4 that, in 3-D flows with a component of the vorticity aligned along the streamlines, the variation of
${x^3}$, which we wish to use as coordinate lines. We then show in § 4 that, in 3-D flows with a component of the vorticity aligned along the streamlines, the variation of ![]() ${\boldsymbol{e}_i}$ along the
${\boldsymbol{e}_i}$ along the ![]() ${x^i}$ lines cannot be completely specified, which limits the utility of a streamline coordinate description in such a case. However, we also show that complex-lamellar flows, that is flows where the mean velocity and mean vorticity are everywhere orthogonal, do admit such a specification. The 2-D flow described by (2.1) and (2.2), together with axially symmetric flows, are the best known cases of complex-lamellar flows but there also exist general 3-D complex-lamellar flows, which form a good approximation to flow in boundary layers and thin shear layers. In such flow fields, we can use the approach described for the 2-D case in F83, where a true coordinate system was first derived and then rescaled to produce physical coordinates. In § 5 we develop the transformation from Cartesian coordinates into a system defined by the intersection of two orthogonal stream surfaces and a modified potential surface, which together form a true coordinate system for general complex-lamellar flow fields. This is a generalisation of the approach described in F83, and from this we derive the corresponding physical equations. In § 6 we derive the physical conservation equation for a general scalar, C. Finally in § 7 we discuss some fundamental differences between these streamline equations and familiar Cartesian equations, particularly inasmuch as deriving small-perturbation approximations as a basis for modelling, leads to different results, according to which equations were used as starting points.
${x^i}$ lines cannot be completely specified, which limits the utility of a streamline coordinate description in such a case. However, we also show that complex-lamellar flows, that is flows where the mean velocity and mean vorticity are everywhere orthogonal, do admit such a specification. The 2-D flow described by (2.1) and (2.2), together with axially symmetric flows, are the best known cases of complex-lamellar flows but there also exist general 3-D complex-lamellar flows, which form a good approximation to flow in boundary layers and thin shear layers. In such flow fields, we can use the approach described for the 2-D case in F83, where a true coordinate system was first derived and then rescaled to produce physical coordinates. In § 5 we develop the transformation from Cartesian coordinates into a system defined by the intersection of two orthogonal stream surfaces and a modified potential surface, which together form a true coordinate system for general complex-lamellar flow fields. This is a generalisation of the approach described in F83, and from this we derive the corresponding physical equations. In § 6 we derive the physical conservation equation for a general scalar, C. Finally in § 7 we discuss some fundamental differences between these streamline equations and familiar Cartesian equations, particularly inasmuch as deriving small-perturbation approximations as a basis for modelling, leads to different results, according to which equations were used as starting points.
3. Flow equations in the Serret–Frenet basis
The momentum equations for the flow of an incompressible fluid can be written as
where ![]() $F_D^k$ represents a body force and the velocity vector u and the fluid stress tensor T are expanded in the orthonormal basis
$F_D^k$ represents a body force and the velocity vector u and the fluid stress tensor T are expanded in the orthonormal basis ![]() ${\boldsymbol{e}_i}$ as
${\boldsymbol{e}_i}$ as
The components of the rates of change of the base vectors ![]() ${\boldsymbol{e}_i}$ along the coordinate lines
${\boldsymbol{e}_i}$ along the coordinate lines ![]() ${x^i}$ are called the connection coefficients
${x^i}$ are called the connection coefficients
where ![]() $\langle ,\rangle $ denotes the inner product. Equation (3.1) expresses the balance between the spatial and temporal acceleration of the flow and the divergence of the stress tensor. The connection coefficients appear because the vector basis
$\langle ,\rangle $ denotes the inner product. Equation (3.1) expresses the balance between the spatial and temporal acceleration of the flow and the divergence of the stress tensor. The connection coefficients appear because the vector basis ![]() ${\boldsymbol{e}_i}$ can change its spatial orientation but not its magnitude as we differentiate vectors and tensors along the coordinate lines. General expressions for gradient, divergence and curl of vectors and tensors in an orthonormal moving frame are given in Appendix A.
${\boldsymbol{e}_i}$ can change its spatial orientation but not its magnitude as we differentiate vectors and tensors along the coordinate lines. General expressions for gradient, divergence and curl of vectors and tensors in an orthonormal moving frame are given in Appendix A.
From hereon we will be concerned with steady flows only. The components of the rate of change of the base vectors in time, ![]() $\varGamma _{jt}^i$, are included in (3.1) for completeness but it is only when such variations can be simply specified that unacceptable complications can be avoided. The only common situation where this is true is in a steadily rotating reference frame such as generates the Coriolis terms on a beta plane. This situation is dealt with in F83 and the results there transfer directly to the 3-D cases considered here. In steady conditions (3.1) becomes
$\varGamma _{jt}^i$, are included in (3.1) for completeness but it is only when such variations can be simply specified that unacceptable complications can be avoided. The only common situation where this is true is in a steadily rotating reference frame such as generates the Coriolis terms on a beta plane. This situation is dealt with in F83 and the results there transfer directly to the 3-D cases considered here. In steady conditions (3.1) becomes
The mean velocity vector ![]() $\boldsymbol{U}$ is aligned with the
$\boldsymbol{U}$ is aligned with the ![]() ${x^1}$ coordinate direction and so its components are
${x^1}$ coordinate direction and so its components are
and the turbulent velocity vector ![]() $\boldsymbol{u}$ has components
$\boldsymbol{u}$ has components
so that the kinematic fluid stress tensor has components
Here, P is the mean kinematic pressure and ![]() ${\delta ^{ij}}$ is the Kronecker delta.
${\delta ^{ij}}$ is the Kronecker delta.
To expand (3.4) we need explicit expressions for the connection coefficients, ![]() $\varGamma _{jk}^i$. Since
$\varGamma _{jk}^i$. Since ![]() ${\boldsymbol{e}_i}$ is orthonormal,
${\boldsymbol{e}_i}$ is orthonormal, ![]() $\langle {\boldsymbol{e}_i},{\boldsymbol{e}_j}\rangle = {\delta _{ij}}$, whence
$\langle {\boldsymbol{e}_i},{\boldsymbol{e}_j}\rangle = {\delta _{ij}}$, whence ![]() $\varGamma _{jk}^i ={-} \varGamma _{ik}^j$ so that,
$\varGamma _{jk}^i ={-} \varGamma _{ik}^j$ so that, ![]() $\varGamma _{\alpha j}^\alpha = 0$ with no sum on Greek indices. From the Serret–Frenet relationships (2.4) we have
$\varGamma _{\alpha j}^\alpha = 0$ with no sum on Greek indices. From the Serret–Frenet relationships (2.4) we have
which leaves six of the nine non-zero connection coefficients undetermined. These are
 \begin{equation}\left. {\begin{array}{@{}l@{}} {\varGamma_{22}^1 ={-} \varGamma_{12}^2,\quad \varGamma_{23}^1 ={-} \varGamma_{13}^2,\quad \varGamma_{32}^1 ={-} \varGamma_{12}^3,}\\ {\varGamma_{33}^1 ={-} \varGamma_{13}^3,\quad \varGamma_{32}^2 ={-} \varGamma_{22}^3,\quad \varGamma_{33}^2 ={-} \varGamma_{23}^3.} \end{array}} \right\}\end{equation}
\begin{equation}\left. {\begin{array}{@{}l@{}} {\varGamma_{22}^1 ={-} \varGamma_{12}^2,\quad \varGamma_{23}^1 ={-} \varGamma_{13}^2,\quad \varGamma_{32}^1 ={-} \varGamma_{12}^3,}\\ {\varGamma_{33}^1 ={-} \varGamma_{13}^3,\quad \varGamma_{32}^2 ={-} \varGamma_{22}^3,\quad \varGamma_{33}^2 ={-} \varGamma_{23}^3.} \end{array}} \right\}\end{equation} To deduce values for these coefficients directly, six independent equations are needed. These are the structure equations of the ![]() ${\boldsymbol{e}_i}$ basis in E3. Finnigan (Reference Finnigan1990) derived and analysed these equations for general 3-D flows and showed that such flows do not admit a simple streamline coordinate description. Before discussing those results, however, it is necessary to distinguish the properties of different flow fields according to whether congruences of their streamlines form integrable manifolds as this is the property which determines the viability of a streamline coordinate description.
${\boldsymbol{e}_i}$ basis in E3. Finnigan (Reference Finnigan1990) derived and analysed these equations for general 3-D flows and showed that such flows do not admit a simple streamline coordinate description. Before discussing those results, however, it is necessary to distinguish the properties of different flow fields according to whether congruences of their streamlines form integrable manifolds as this is the property which determines the viability of a streamline coordinate description.
4. Classification of flows
4.1. Classifying flows topologically using the Frobenius integral theorem
As a first step, we derive expressions for the divergence and curl of the flow in the ![]() ${\boldsymbol{e}_i}$ basis. In the Cartesian reference frame
${\boldsymbol{e}_i}$ basis. In the Cartesian reference frame ![]() ${y^i}$, the spatial variation of the mean velocity field is described by the flow deformation tensor
${y^i}$, the spatial variation of the mean velocity field is described by the flow deformation tensor ![]() $\partial {U^i}/\partial {y^j}$. This may be split into symmetric and skew symmetric parts
$\partial {U^i}/\partial {y^j}$. This may be split into symmetric and skew symmetric parts
where ![]() ${s^{ij}}$ is the rate of strain tensor while the elements of
${s^{ij}}$ is the rate of strain tensor while the elements of ![]() ${a^{ij}}$, the rotation tensor, are
${a^{ij}}$, the rotation tensor, are ![]() ${\varOmega ^i}$, the components of the vorticity vector
${\varOmega ^i}$, the components of the vorticity vector ![]() $\boldsymbol{\varOmega } = \boldsymbol{\nabla } \wedge \boldsymbol{U}$;
$\boldsymbol{\varOmega } = \boldsymbol{\nabla } \wedge \boldsymbol{U}$; ![]() ${s^{ij}}$ is a real symmetric second-order tensor, and so has three scalar invariants. These ‘Cayley–Hamilton’ invariants are the coefficients of the characteristic equation of
${s^{ij}}$ is a real symmetric second-order tensor, and so has three scalar invariants. These ‘Cayley–Hamilton’ invariants are the coefficients of the characteristic equation of ![]() ${s^{ij}}$. Two of these invariants have no simple physical meaning (Dishington Reference Dishington1960) but the third is the trace of
${s^{ij}}$. Two of these invariants have no simple physical meaning (Dishington Reference Dishington1960) but the third is the trace of ![]() ${s^{ij}}$, where
${s^{ij}}$, where ![]() $\textrm{Tr}({s^{ij}}) = {s^{ii}} = \boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{U}$. Using the general expression for the divergence in an orthonormal moving frame (Appendix A), we obtain
$\textrm{Tr}({s^{ij}}) = {s^{ii}} = \boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{U}$. Using the general expression for the divergence in an orthonormal moving frame (Appendix A), we obtain
In the ![]() ${\boldsymbol{e}_i}$ basis, the mean flow vorticity
${\boldsymbol{e}_i}$ basis, the mean flow vorticity ![]() $\boldsymbol{\varOmega} $ becomes
$\boldsymbol{\varOmega} $ becomes
where A is the abnormality of the field of ![]() ${\boldsymbol{e}_1}$ vectors
${\boldsymbol{e}_1}$ vectors
and
so
Similarly, we can write the curls and abnormalities of the fields of principal normal ![]() ${\boldsymbol{e}^2}$ and binormal
${\boldsymbol{e}^2}$ and binormal ![]() ${\boldsymbol{e}^3}$ vectors as
${\boldsymbol{e}^3}$ vectors as
so
so
Hence
We see from (4.5)–(4.8) that the link between the abnormality of the ![]() ${\boldsymbol{e}_1}$ field and the torsion of the mean streamlines
${\boldsymbol{e}_1}$ field and the torsion of the mean streamlines ![]() ${x^1}$ is mediated by the abnormalities of the principal normal and binormal fields. We also note that when a field of base vectors
${x^1}$ is mediated by the abnormalities of the principal normal and binormal fields. We also note that when a field of base vectors ![]() ${\boldsymbol{e}_\alpha }$ has non-zero abnormality, the curl of
${\boldsymbol{e}_\alpha }$ has non-zero abnormality, the curl of ![]() ${\boldsymbol{e}_\alpha }$ will have a component
${\boldsymbol{e}_\alpha }$ will have a component ![]() $\varGamma _{\beta \gamma }^\alpha {\boldsymbol{e}_\alpha }$ with
$\varGamma _{\beta \gamma }^\alpha {\boldsymbol{e}_\alpha }$ with ![]() $\alpha ,\;\beta ,\;\gamma $ all different.
$\alpha ,\;\beta ,\;\gamma $ all different.
We are now able to use the vector form of the Frobenius integral theorem (Schutz Reference Schutz1980) to classify different flow fields. This theorem states that, if we have space curves, ![]() ${x^i}$, defined by the intersections of constant surfaces in space, which are differentiable manifolds, the partial derivatives
${x^i}$, defined by the intersections of constant surfaces in space, which are differentiable manifolds, the partial derivatives ![]() $\partial /\partial {x^i}$ form a vector basis because these vectors automatically commute, i.e.
$\partial /\partial {x^i}$ form a vector basis because these vectors automatically commute, i.e.
However, if we choose an arbitrary vector basis, for example the non-coordinate physical basis ![]() ${\boldsymbol{e}_i}$ formed from the directional derivatives of the reparametrised coordinate lines as in the physical 2-D equations (2.1) and (2.2), these vectors do not, in general, commute
${\boldsymbol{e}_i}$ formed from the directional derivatives of the reparametrised coordinate lines as in the physical 2-D equations (2.1) and (2.2), these vectors do not, in general, commute
The commutator or Lie bracket (4.10) defines a vector field and so can itself be expanded in the coordinate basis ![]() $\partial /\partial {x^i}$
$\partial /\partial {x^i}$
The tangent planes of the coordinate base vectors, ![]() $\partial /\partial {x^i}$, taken in pairs, foliate the integrable manifolds whose intersections define the coordinate lines
$\partial /\partial {x^i}$, taken in pairs, foliate the integrable manifolds whose intersections define the coordinate lines ![]() ${x^i}$ (Schutz Reference Schutz1980). If
${x^i}$ (Schutz Reference Schutz1980). If ![]() ${\boldsymbol{e}_i}$ were obtained by rescaling the coordinate basis
${\boldsymbol{e}_i}$ were obtained by rescaling the coordinate basis ![]() $\partial /\partial {x^i}$, then the tangent planes of the
$\partial /\partial {x^i}$, then the tangent planes of the ![]() ${\boldsymbol{e}_i}$ base vectors, taken in pairs, must be parallel to the coordinate basis tangent planes. For this to be true, the commutator of
${\boldsymbol{e}_i}$ base vectors, taken in pairs, must be parallel to the coordinate basis tangent planes. For this to be true, the commutator of ![]() ${\partial _1}$ and
${\partial _1}$ and ![]() ${\partial _2}$ must have no component in the
${\partial _2}$ must have no component in the ![]() $\partial /\partial {x^3}$ or
$\partial /\partial {x^3}$ or ![]() ${\partial _3}$ direction, i.e. it must lie in the plane spanned by
${\partial _3}$ direction, i.e. it must lie in the plane spanned by ![]() $\partial /\partial {x^1}$ and
$\partial /\partial {x^1}$ and ![]() $\partial /\partial {x^2}$, or equivalently, by
$\partial /\partial {x^2}$, or equivalently, by ![]() ${\partial _1}$ and
${\partial _1}$ and ![]() ${\partial _2}$, and the same goes for the other commutators:
${\partial _2}$, and the same goes for the other commutators: ![]() $[{\partial _1},{\partial _3}]$ can have no component in the
$[{\partial _1},{\partial _3}]$ can have no component in the ![]() $\partial /\partial {x^2}$ or
$\partial /\partial {x^2}$ or ![]() ${\partial _2}$ direction and
${\partial _2}$ direction and ![]() $[{\partial _2},{\partial _3}]$can have no component in the
$[{\partial _2},{\partial _3}]$can have no component in the ![]() $\partial /\partial {x^1}$ or
$\partial /\partial {x^1}$ or ![]() ${\partial _1}$ direction. The converse is also true. If the commutators of the
${\partial _1}$ direction. The converse is also true. If the commutators of the ![]() ${\boldsymbol{e}_i}$ base vectors, taken in pairs, have components that do not lie in the plane spanned by the pairs of partial derivatives, they cannot be derived by scaling a true coordinate system.
${\boldsymbol{e}_i}$ base vectors, taken in pairs, have components that do not lie in the plane spanned by the pairs of partial derivatives, they cannot be derived by scaling a true coordinate system.
We now apply the Frobenius theorem to the Serret–Frenet basis, ![]() ${\boldsymbol{e}_i}$. Following (4.10), the components of the commutator
${\boldsymbol{e}_i}$. Following (4.10), the components of the commutator ![]() $[{\boldsymbol{e}_i},{\boldsymbol{e}_j}]$ are
$[{\boldsymbol{e}_i},{\boldsymbol{e}_j}]$ are
Evidently, from (4.5)–(4.8), when the flow has a component of mean vorticity in the ![]() ${x^1}$, direction, the streamlines are twisted curves with
${x^1}$, direction, the streamlines are twisted curves with ![]() $1/\sigma \ne 0$ and the integral curves of the principal and binormal fields
$1/\sigma \ne 0$ and the integral curves of the principal and binormal fields ![]() ${x^2},\;{x^3}$ are also twisted curves so that the coefficients of
${x^2},\;{x^3}$ are also twisted curves so that the coefficients of ![]() ${\boldsymbol{e}^i}$ in (4.12a–c), which involve
${\boldsymbol{e}^i}$ in (4.12a–c), which involve ![]() $\varGamma _{jk}^i$ terms with
$\varGamma _{jk}^i$ terms with ![]() $i,\;j,\;k$ all different, are non-zero. As a result, the commutator of any pair of bases,
$i,\;j,\;k$ all different, are non-zero. As a result, the commutator of any pair of bases, ![]() $[{\boldsymbol{e}_\alpha },{\boldsymbol{e}_\beta }]$ has a component in the
$[{\boldsymbol{e}_\alpha },{\boldsymbol{e}_\beta }]$ has a component in the ![]() ${\boldsymbol{e}_\gamma }$ direction, signalled by the appearance of the coefficient of
${\boldsymbol{e}_\gamma }$ direction, signalled by the appearance of the coefficient of ![]() ${\boldsymbol{e}_\gamma }$ being
${\boldsymbol{e}_\gamma }$ being ![]() $\varGamma _{\alpha \beta }^\gamma \ne 0$. Hence, the commutators of the Serret–Frenet basis in a general 3-D flow field do not lie in the tangent planes spanned by the base vectors and the basis cannot be derived by rescaling an underlying coordinate basis.
$\varGamma _{\alpha \beta }^\gamma \ne 0$. Hence, the commutators of the Serret–Frenet basis in a general 3-D flow field do not lie in the tangent planes spanned by the base vectors and the basis cannot be derived by rescaling an underlying coordinate basis.
In the 2-D case treated in F83, the streamlines are confined to the planes of symmetry and so are plane curves with ![]() $1/\sigma = 0$. In such flows, the only component of the mean vorticity vector,
$1/\sigma = 0$. In such flows, the only component of the mean vorticity vector, ![]() $\boldsymbol{\varOmega } = \{ {\varOmega ^1},{\varOmega ^2},{\varOmega ^3}\} $ is
$\boldsymbol{\varOmega } = \{ {\varOmega ^1},{\varOmega ^2},{\varOmega ^3}\} $ is ![]() ${\varOmega ^3} = (U/R - {\partial _2}U)$ and is aligned with the
${\varOmega ^3} = (U/R - {\partial _2}U)$ and is aligned with the ![]() ${\boldsymbol{e}_3}$ base vector or the rectilinear
${\boldsymbol{e}_3}$ base vector or the rectilinear ![]() ${x^3}$ coordinate line. Flows with
${x^3}$ coordinate line. Flows with ![]() $\langle \boldsymbol{U},\boldsymbol{\varOmega }\rangle = 0$, are known as complex-lamellar flows, that is, the vorticity is everywhere normal to the velocity (Aris Reference Aris1962). As discussed in F83 and references therein, complex-lamellar flows admit a normal congruence of surfaces, the desirable property that allowed the use of
$\langle \boldsymbol{U},\boldsymbol{\varOmega }\rangle = 0$, are known as complex-lamellar flows, that is, the vorticity is everywhere normal to the velocity (Aris Reference Aris1962). As discussed in F83 and references therein, complex-lamellar flows admit a normal congruence of surfaces, the desirable property that allowed the use of ![]() $\phi ({\kern0.9pt}\boldsymbol{y})$,
$\phi ({\kern0.9pt}\boldsymbol{y})$, ![]() $\psi ({\kern0.9pt}\boldsymbol{y})$ and the planes of symmetry as orthogonal coordinate surfaces and the generation of an orthogonal physical coordinate system, with the advantages of interpretation that confers. While the most familiar examples of complex-lamellar flows are two-dimensional and axisymmetric, these do not exhaust the class of such flows and in the next § 5, we develop first true then physical coordinate systems for general 3-D complex-lamellar flows. First, however, we make some observations on general 3-D flows where
$\psi ({\kern0.9pt}\boldsymbol{y})$ and the planes of symmetry as orthogonal coordinate surfaces and the generation of an orthogonal physical coordinate system, with the advantages of interpretation that confers. While the most familiar examples of complex-lamellar flows are two-dimensional and axisymmetric, these do not exhaust the class of such flows and in the next § 5, we develop first true then physical coordinate systems for general 3-D complex-lamellar flows. First, however, we make some observations on general 3-D flows where ![]() $\langle \boldsymbol{U},\boldsymbol{\varOmega }\rangle \ne 0$.
$\langle \boldsymbol{U},\boldsymbol{\varOmega }\rangle \ne 0$.
4.2. Flow equations in the general three-dimensional case
Finnigan (Reference Finnigan1990) notes that there are two related properties that prevent the moving frame ![]() ${\boldsymbol{e}_i}$, attached to the twisted streamlines of flows where
${\boldsymbol{e}_i}$, attached to the twisted streamlines of flows where ![]() $\langle \boldsymbol{U},\boldsymbol{\varOmega }\rangle \ne 0$, from forming a useful coordinate system. The first is that the congruence of streamlines that pass through a trace formed by an arbitrary space curve
$\langle \boldsymbol{U},\boldsymbol{\varOmega }\rangle \ne 0$, from forming a useful coordinate system. The first is that the congruence of streamlines that pass through a trace formed by an arbitrary space curve ![]() $\varphi ({\kern0.9pt}\boldsymbol{y})$ do not form an integrable manifold, as we saw above. In practical terms, this means that we cannot find general solutions of the structure equations that determine all the
$\varphi ({\kern0.9pt}\boldsymbol{y})$ do not form an integrable manifold, as we saw above. In practical terms, this means that we cannot find general solutions of the structure equations that determine all the ![]() $\varGamma _{jk}^i$. This conclusion is reviewed briefly in Appendix B. The second is that the basis
$\varGamma _{jk}^i$. This conclusion is reviewed briefly in Appendix B. The second is that the basis ![]() ${\boldsymbol{e}_i}$ is not orientable (Spivak Reference Spivak1979, Vol. 2) so that the defination of the positive direction along the coordinate lines, which are the integral curves of
${\boldsymbol{e}_i}$ is not orientable (Spivak Reference Spivak1979, Vol. 2) so that the defination of the positive direction along the coordinate lines, which are the integral curves of ![]() ${\boldsymbol{e}_i}$, is indeterminate. In the 2-D case of F83, where the streamlines are plane curves, the basis is orientable so that the curvature
${\boldsymbol{e}_i}$, is indeterminate. In the 2-D case of F83, where the streamlines are plane curves, the basis is orientable so that the curvature ![]() $1/R$ is a signed quantity defined as +ve (−ve) if the centre of curvature of the streamline lies in the +ve (−ve)
$1/R$ is a signed quantity defined as +ve (−ve) if the centre of curvature of the streamline lies in the +ve (−ve) ![]() ${x^2}$ direction. Taking
${x^2}$ direction. Taking ![]() ${\boldsymbol{e}_i}$ as a right-handed system then defines the other coordinate directions. When the streamlines are twisted curves, the torsion
${\boldsymbol{e}_i}$ as a right-handed system then defines the other coordinate directions. When the streamlines are twisted curves, the torsion ![]() $1/\sigma $ can be interpreted as the rate at which the
$1/\sigma $ can be interpreted as the rate at which the ![]() ${\boldsymbol{e}_2}$ and
${\boldsymbol{e}_2}$ and ![]() ${\boldsymbol{e}_3}$ base vectors, which are confined to the normal plane, rotate around the
${\boldsymbol{e}_3}$ base vectors, which are confined to the normal plane, rotate around the ![]() ${\boldsymbol{e}_1}$ vector as
${\boldsymbol{e}_1}$ vector as ![]() ${x^1}$ changes (Aris Reference Aris1962). As a consequence, whenever
${x^1}$ changes (Aris Reference Aris1962). As a consequence, whenever ![]() $1/\sigma $ changes sign, the coordinate directions will reverse.
$1/\sigma $ changes sign, the coordinate directions will reverse.
Surprisingly, despite these limitations, the full ![]() ${\boldsymbol{e}_i}$ moving frame equations do reveal an interesting property of general flows, as we can see in the momentum equations written in the
${\boldsymbol{e}_i}$ moving frame equations do reveal an interesting property of general flows, as we can see in the momentum equations written in the ![]() ${\boldsymbol{e}_i}$ basis. Accepting that we cannot specify four of the connection coefficients,
${\boldsymbol{e}_i}$ basis. Accepting that we cannot specify four of the connection coefficients, ![]() $\varGamma _{22}^1,\;\varGamma _{33}^1,\;\varGamma _{33}^2,\;\varGamma _{22}^3$ the streamwise
$\varGamma _{22}^1,\;\varGamma _{33}^1,\;\varGamma _{33}^2,\;\varGamma _{22}^3$ the streamwise ![]() ${x^1}$ direction equation becomes
${x^1}$ direction equation becomes
 \begin{align} U{\partial _1}U &= \dfrac{{{U^2}}}{{{L_a}}} ={-} {\partial _1}P - {\partial _1}\overline {{u^1}{u^1}} - {\partial _2}\overline {{u^1}{u^2}} - {\partial _3}\overline {{u^1}{u^3}}+ \overline {{u^1}{u^1}} \dfrac{1}{{{L_a}}}- \overline {{u^2}{u^2}} \varGamma _{22}^1 \nonumber\\ & \quad - \overline {{u^3}{u^3}} \varGamma _{33}^1 + \overline {{u^1}{u^2}} \left( {\dfrac{2}{R} + \varGamma_{33}^2} \right) + \overline {{u^1}{u^3}} \varGamma _{22}^3 + F_D^1 + \textrm{viscous}\;\textrm{terms,} \end{align}
\begin{align} U{\partial _1}U &= \dfrac{{{U^2}}}{{{L_a}}} ={-} {\partial _1}P - {\partial _1}\overline {{u^1}{u^1}} - {\partial _2}\overline {{u^1}{u^2}} - {\partial _3}\overline {{u^1}{u^3}}+ \overline {{u^1}{u^1}} \dfrac{1}{{{L_a}}}- \overline {{u^2}{u^2}} \varGamma _{22}^1 \nonumber\\ & \quad - \overline {{u^3}{u^3}} \varGamma _{33}^1 + \overline {{u^1}{u^2}} \left( {\dfrac{2}{R} + \varGamma_{33}^2} \right) + \overline {{u^1}{u^3}} \varGamma _{22}^3 + F_D^1 + \textrm{viscous}\;\textrm{terms,} \end{align}
where ![]() ${L_a}$, as defined in (4.2), is the e-folding distance of streamwise acceleration as in the 2-D equations but is no longer the radius of curvature of the
${L_a}$, as defined in (4.2), is the e-folding distance of streamwise acceleration as in the 2-D equations but is no longer the radius of curvature of the ![]() ${x^2}$ coordinate lines. The momentum equation in the principal normal
${x^2}$ coordinate lines. The momentum equation in the principal normal ![]() ${x^2}$ direction is
${x^2}$ direction is
 \begin{align}
\dfrac{{{U^2}}}{R} & ={-} {\partial _2}P - {\partial
_1}\overline {{u^1}{u^2}} - {\partial _2}\overline
{{u^2}{u^2}} - {\partial _3}\overline {{u^2}{u^3}}\nonumber \\
& \quad - (\overline {{u^1}{u^1}} - \overline {{u^2}{u^2}}
)\dfrac{1}{R} - (\overline {{u^3}{u^3}} - \overline
{{u^2}{u^2}} )\varGamma _{33}^2 + \overline {{u^1}{u^2}}
\varGamma _{22}^1\nonumber\\
& \quad + \overline {{u^1}{u^2}}
\dfrac{1}{{{L_a}}} + \overline {{u^2}{u^3}} 2\varGamma
_{22}^3 + F_D^2 + \textrm{viscous}\;\textrm{terms,}
\end{align}
\begin{align}
\dfrac{{{U^2}}}{R} & ={-} {\partial _2}P - {\partial
_1}\overline {{u^1}{u^2}} - {\partial _2}\overline
{{u^2}{u^2}} - {\partial _3}\overline {{u^2}{u^3}}\nonumber \\
& \quad - (\overline {{u^1}{u^1}} - \overline {{u^2}{u^2}}
)\dfrac{1}{R} - (\overline {{u^3}{u^3}} - \overline
{{u^2}{u^2}} )\varGamma _{33}^2 + \overline {{u^1}{u^2}}
\varGamma _{22}^1\nonumber\\
& \quad + \overline {{u^1}{u^2}}
\dfrac{1}{{{L_a}}} + \overline {{u^2}{u^3}} 2\varGamma
_{22}^3 + F_D^2 + \textrm{viscous}\;\textrm{terms,}
\end{align}
where in this case R is still the local radius of curvature of the streamline when measured in the osculating plane spanned by the ![]() ${\boldsymbol{e}_1}$ and
${\boldsymbol{e}_1}$ and ![]() ${\boldsymbol{e}_2}$ base vectors. The
${\boldsymbol{e}_2}$ base vectors. The ![]() ${x^3}$ binormal direction equation is
${x^3}$ binormal direction equation is
 \begin{align} 0 &
={-} {\partial _3}P - {\partial _1}\overline {{u^1}{u^3}} -
{\partial _2}\overline {{u^2}{u^3}} - {\partial
_3}\overline {{u^3}{u^3}} - (\overline {{u^2}{u^2}} -
\overline {{u^3}{u^3}} )\varGamma _{22}^3\nonumber\\
& \quad + \overline {{u^1}{u^3}} \dfrac{1}{{{L_a}}} + \overline
{{u^1}{u^3}} \varGamma _{33}^1 - \overline {{u^2}{u^3}}
\left( {2\varGamma_{23}^3 - \dfrac{1}{R}} \right) +
F_D^3 + \textrm{viscous}\;\textrm{terms}.
\end{align}
\begin{align} 0 &
={-} {\partial _3}P - {\partial _1}\overline {{u^1}{u^3}} -
{\partial _2}\overline {{u^2}{u^3}} - {\partial
_3}\overline {{u^3}{u^3}} - (\overline {{u^2}{u^2}} -
\overline {{u^3}{u^3}} )\varGamma _{22}^3\nonumber\\
& \quad + \overline {{u^1}{u^3}} \dfrac{1}{{{L_a}}} + \overline
{{u^1}{u^3}} \varGamma _{33}^1 - \overline {{u^2}{u^3}}
\left( {2\varGamma_{23}^3 - \dfrac{1}{R}} \right) +
F_D^3 + \textrm{viscous}\;\textrm{terms}.
\end{align}(Note that in (4.13), (4.14) and (4.15), for brevity we have not written out the viscous stress divergence in full as its inclusion does not affect the following argument.)
These equations reveal an important result. As in the 2-D case, the ![]() ${x^1}$ equation captures all the information about the linear momentum of the flow. The inertial acceleration
${x^1}$ equation captures all the information about the linear momentum of the flow. The inertial acceleration ![]() $U{\partial _1}U = {U^2}/{L_a}$ is balanced by the streamwise pressure gradient
$U{\partial _1}U = {U^2}/{L_a}$ is balanced by the streamwise pressure gradient ![]() ${\partial _1}P$ and the
${\partial _1}P$ and the ![]() ${x^1}$ component of the stress divergence plus any body force in the
${x^1}$ component of the stress divergence plus any body force in the ![]() ${x^1}$ direction. The
${x^1}$ direction. The ![]() ${x^2}$ equation captures all the information about the angular momentum of the flow. The centrifugal acceleration
${x^2}$ equation captures all the information about the angular momentum of the flow. The centrifugal acceleration ![]() ${U^2}/R$ is balanced by the pressure gradient in the direction of the principal normal to the streamline, the direction in which the streamline has its maximum curvature, and the
${U^2}/R$ is balanced by the pressure gradient in the direction of the principal normal to the streamline, the direction in which the streamline has its maximum curvature, and the ![]() ${x^2}$ component of the stress divergence plus any body force in the
${x^2}$ component of the stress divergence plus any body force in the ![]() ${x^2}$ direction. There is no other form of momentum so that the
${x^2}$ direction. There is no other form of momentum so that the ![]() ${x^3}$ equation tells us that any pressure gradient in the binormal direction must be balanced by the stress divergence and body force as there is no inertial acceleration in the
${x^3}$ equation tells us that any pressure gradient in the binormal direction must be balanced by the stress divergence and body force as there is no inertial acceleration in the ![]() ${x^3}$ direction. If we were considering an inviscid non-turbulent fluid obeying Euler's equations, the three equations would take the form
${x^3}$ direction. If we were considering an inviscid non-turbulent fluid obeying Euler's equations, the three equations would take the form
So there can be no mean pressure gradient in the binormal direction in a steady inviscid flow without a body force. At first sight this result seems counter-intuitive as we might expect that streamline divergence as the flow approaches a solid obstacle would be caused by a pressure gradient acting along the ![]() ${x^3}$ direction to move streamlines apart but a simple counter-example shows this is not necessary. Consider irrotational flow approaching a body of revolution like a sphere. The streamlines diverge from the stagnation streamline as they pass around the sphere but in axially symmetric streamline coordinates (Finnigan Reference Finnigan1990), the
${x^3}$ direction to move streamlines apart but a simple counter-example shows this is not necessary. Consider irrotational flow approaching a body of revolution like a sphere. The streamlines diverge from the stagnation streamline as they pass around the sphere but in axially symmetric streamline coordinates (Finnigan Reference Finnigan1990), the ![]() ${x^3}$ lines are circles around the stagnation streamline and symmetry demands that there can be no mean gradients in the
${x^3}$ lines are circles around the stagnation streamline and symmetry demands that there can be no mean gradients in the ![]() ${x^3}$ direction. Pressure gradients do play a role because adjacent streamlines are decelerated to differing degrees depending on their distance from the obstacle. This causes shear in the cross-streamline
${x^3}$ direction. Pressure gradients do play a role because adjacent streamlines are decelerated to differing degrees depending on their distance from the obstacle. This causes shear in the cross-streamline ![]() ${x^2}$ direction but, in an inviscid flow,
${x^2}$ direction but, in an inviscid flow, ![]() ${\varOmega ^3} = U/R - {\partial _2}U = 0$ and the shear is compensated by streamline curvature, which takes the flow around the sphere. In viscous and turbulent flows, there may well be a non-zero
${\varOmega ^3} = U/R - {\partial _2}U = 0$ and the shear is compensated by streamline curvature, which takes the flow around the sphere. In viscous and turbulent flows, there may well be a non-zero ![]() ${\partial _3}P$ as the flow negotiates obstacles but this is not essential and must be the result of stress divergence and body forces.
${\partial _3}P$ as the flow negotiates obstacles but this is not essential and must be the result of stress divergence and body forces.
5. A description of general three-dimensional complex-lamellar flows
5.1. Complex-lamellar boundary layer flows
For flow over a solid surface, the expression for mean vorticity (4.3) in the Serret–Frenet basis ![]() ${\boldsymbol{e}_i}$, orientated so that the
${\boldsymbol{e}_i}$, orientated so that the ![]() ${\boldsymbol{e}_2}$ base vectors intersect the surface normally and the
${\boldsymbol{e}_2}$ base vectors intersect the surface normally and the ![]() ${\boldsymbol{e}_1}$ and
${\boldsymbol{e}_1}$ and ![]() ${\boldsymbol{e}_3}$ base vectors are in the tangent planes parallel to the surface, takes the form
${\boldsymbol{e}_3}$ base vectors are in the tangent planes parallel to the surface, takes the form
The no-slip condition then ensures that as ![]() ${x^2} \to 0$,
${x^2} \to 0$, ![]() $(UA) \to 0$,
$(UA) \to 0$, ![]() $({\partial _3}U) \to 0$. In boundary layer flows, by definition,
$({\partial _3}U) \to 0$. In boundary layer flows, by definition, ![]() ${\partial _2}U \gg {\partial _1}U,\;{\partial _3}U$ so that in this region, the vorticity becomes,
${\partial _2}U \gg {\partial _1}U,\;{\partial _3}U$ so that in this region, the vorticity becomes, ![]() $\boldsymbol{\nabla } \wedge \boldsymbol{U} \simeq 0{\boldsymbol{e}_1} + 0{\boldsymbol{e}_2} + (U/R - {\partial _2}U){\boldsymbol{e}_3}$ and the flow becomes approximately complex lamellar. Similar scaling arguments apply equally to thin shear layers as long as the
$\boldsymbol{\nabla } \wedge \boldsymbol{U} \simeq 0{\boldsymbol{e}_1} + 0{\boldsymbol{e}_2} + (U/R - {\partial _2}U){\boldsymbol{e}_3}$ and the flow becomes approximately complex lamellar. Similar scaling arguments apply equally to thin shear layers as long as the ![]() ${\boldsymbol{e}_i}$ basis is orientated appropriately. Complex-lamellar flows are, therefore, a useful approximation to many practical situations such as atmospheric boundary layer flow over gentle topography or non-separating boundary layers in engineering applications. In the next section, therefore, we develop true and physical coordinate descriptions of general 3-D complex-lamellar flows
${\boldsymbol{e}_i}$ basis is orientated appropriately. Complex-lamellar flows are, therefore, a useful approximation to many practical situations such as atmospheric boundary layer flow over gentle topography or non-separating boundary layers in engineering applications. In the next section, therefore, we develop true and physical coordinate descriptions of general 3-D complex-lamellar flows
5.2. Coordinates for three-dimensional complex-lamellar flow
5.2.1. Stream surfaces and normal surfaces
Along a streamline, the velocity components ![]() ${U^i}$ in the Cartesian reference frame
${U^i}$ in the Cartesian reference frame ![]() $\boldsymbol{y}$ obey the equation
$\boldsymbol{y}$ obey the equation
The solution of this type of first-order differential equation was of great interest to mathematicians of the 18th and 19th centuries and is usually referred to as Pfaff's problem (Ince Reference Ince1956; Piaggio Reference Piaggio1958). A solution to (5.2) consists of the intersection of two stream surfaces, ![]() $f({\kern0.9pt}\boldsymbol{y}) = \textrm{constant}$,
$f({\kern0.9pt}\boldsymbol{y}) = \textrm{constant}$, ![]() $g({\kern0.9pt}\boldsymbol{y}) = \textrm{constant}$ and Yih (Reference Yih1977) shows that, without loss of generality, the values of f and g can be chosen so that
$g({\kern0.9pt}\boldsymbol{y}) = \textrm{constant}$ and Yih (Reference Yih1977) shows that, without loss of generality, the values of f and g can be chosen so that
For complex-lamellar flows there exists a normal congruence of surfaces and we can define f and g as two of these so that ![]() $\langle \boldsymbol{\nabla }f,\boldsymbol{\nabla }g\rangle = 0$. We obtain the third normal surface as the solution of
$\langle \boldsymbol{\nabla }f,\boldsymbol{\nabla }g\rangle = 0$. We obtain the third normal surface as the solution of ![]() $\langle \boldsymbol{u},\textrm{d}\kern0.07em\boldsymbol{x}\rangle = 0$, which is simply a restatement of (5.2) and, since the flow is complex lamellar, we can find an integrating factor
$\langle \boldsymbol{u},\textrm{d}\kern0.07em\boldsymbol{x}\rangle = 0$, which is simply a restatement of (5.2) and, since the flow is complex lamellar, we can find an integrating factor ![]() $\zeta ({\kern0.9pt}\boldsymbol{y})$ such that
$\zeta ({\kern0.9pt}\boldsymbol{y})$ such that
is exact so
The surface ![]() $\phi ({\kern0.9pt}\boldsymbol{y}) = \textrm{constant}$ is normal to f and g. We are free to choose the orientation of f and g around the streamline and we have shown in (4.12) that in a complex-lamellar flow we can choose surfaces that are integrable manifolds and whose tangent planes are parallel to those spanned by the Serret–Frenet base vectors so we identify the
$\phi ({\kern0.9pt}\boldsymbol{y}) = \textrm{constant}$ is normal to f and g. We are free to choose the orientation of f and g around the streamline and we have shown in (4.12) that in a complex-lamellar flow we can choose surfaces that are integrable manifolds and whose tangent planes are parallel to those spanned by the Serret–Frenet base vectors so we identify the ![]() $\phi ({\kern0.9pt}\boldsymbol{y})$,
$\phi ({\kern0.9pt}\boldsymbol{y})$, ![]() $g({\kern0.9pt}\boldsymbol{y})$ and
$g({\kern0.9pt}\boldsymbol{y})$ and ![]() $f({\kern0.9pt}\boldsymbol{y})$ surfaces as a true orthogonal coordinate system for general complex-lamellar flow. The coordinate lines
$f({\kern0.9pt}\boldsymbol{y})$ surfaces as a true orthogonal coordinate system for general complex-lamellar flow. The coordinate lines ![]() ${x^i}$ are now the intersections of constant
${x^i}$ are now the intersections of constant ![]() $\phi ,\;g,\;\textrm{and}\;f$ surfaces. We choose the
$\phi ,\;g,\;\textrm{and}\;f$ surfaces. We choose the ![]() $f = \textrm{constant}$ surface as that whose tangent planes are parallel to the Serret–Frenet osculating planes so that the value of f increases along the
$f = \textrm{constant}$ surface as that whose tangent planes are parallel to the Serret–Frenet osculating planes so that the value of f increases along the ![]() ${x^3}$ coordinate lines. Similarly, the
${x^3}$ coordinate lines. Similarly, the ![]() $g = \textrm{constant}$ surface has its tangent planes parallel to the Serret–Frenet tangent planes so that the value of g increases along the
$g = \textrm{constant}$ surface has its tangent planes parallel to the Serret–Frenet tangent planes so that the value of g increases along the ![]() ${x^2}$ coordinate lines and the
${x^2}$ coordinate lines and the ![]() $\phi = \textrm{constant}$ surface has its tangent planes parallel to the Serret–Frenet normal planes so that the value of
$\phi = \textrm{constant}$ surface has its tangent planes parallel to the Serret–Frenet normal planes so that the value of ![]() $\phi $ increases along the
$\phi $ increases along the ![]() ${x^1}$ coordinate lines. The base vectors
${x^1}$ coordinate lines. The base vectors ![]() $\partial /\partial \phi$,
$\partial /\partial \phi$, ![]() $\partial /\partial g$,
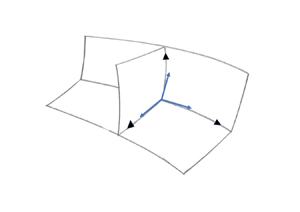
$\partial /\partial g$, ![]() $\partial /\partial f$ are tangent to the coordinate lines and parallel to the tangent, principal normal and binormal to the streamline. The system is shown graphically in figure 2.
$\partial /\partial f$ are tangent to the coordinate lines and parallel to the tangent, principal normal and binormal to the streamline. The system is shown graphically in figure 2.

Figure 2. Coordinate surfaces and base vectors in the 3-D streamline coordinate system.
To complete the specification of this system we need to define ![]() $\zeta ({\kern0.9pt}\boldsymbol{y})$. From (5.3) and (5.4), we can write
$\zeta ({\kern0.9pt}\boldsymbol{y})$. From (5.3) and (5.4), we can write
 \begin{equation}\left.
{\begin{array}{@{}c@{}} {\boldsymbol{U} =
\boldsymbol{\nabla }f \wedge \boldsymbol{\nabla }g \to
\boldsymbol{U} = \boldsymbol{\nabla } \wedge
(f\boldsymbol{\nabla }g) = \boldsymbol{\nabla } \wedge
\varPsi ,}\\ {\boldsymbol{\nabla }\phi = \zeta
\boldsymbol{U} = \zeta (\boldsymbol{\nabla } \wedge \varPsi
),}\\ {\boldsymbol{\nabla } \wedge \boldsymbol{\nabla }\phi
= 0 \to \boldsymbol{\nabla } \wedge (\zeta
\,\boldsymbol{\nabla } \wedge \varPsi ) =
\boldsymbol{\nabla } \wedge \zeta \boldsymbol{U} = 0,}\\
{\boldsymbol{\nabla } \wedge \zeta \boldsymbol{U} = \zeta
\,\boldsymbol{\nabla } \wedge \boldsymbol{U} +
\boldsymbol{\nabla }\zeta \wedge \boldsymbol{U} = 0,}\\
{\boldsymbol{\nabla } \wedge \boldsymbol{U} = \boldsymbol{\varOmega}
,\;\textrm{and}\;\textrm{so,}\;\zeta \,\boldsymbol{\varOmega} +
\boldsymbol{\nabla }\zeta \wedge \boldsymbol{U} = 0,}
\end{array}}
\right\}\end{equation}
\begin{equation}\left.
{\begin{array}{@{}c@{}} {\boldsymbol{U} =
\boldsymbol{\nabla }f \wedge \boldsymbol{\nabla }g \to
\boldsymbol{U} = \boldsymbol{\nabla } \wedge
(f\boldsymbol{\nabla }g) = \boldsymbol{\nabla } \wedge
\varPsi ,}\\ {\boldsymbol{\nabla }\phi = \zeta
\boldsymbol{U} = \zeta (\boldsymbol{\nabla } \wedge \varPsi
),}\\ {\boldsymbol{\nabla } \wedge \boldsymbol{\nabla }\phi
= 0 \to \boldsymbol{\nabla } \wedge (\zeta
\,\boldsymbol{\nabla } \wedge \varPsi ) =
\boldsymbol{\nabla } \wedge \zeta \boldsymbol{U} = 0,}\\
{\boldsymbol{\nabla } \wedge \zeta \boldsymbol{U} = \zeta
\,\boldsymbol{\nabla } \wedge \boldsymbol{U} +
\boldsymbol{\nabla }\zeta \wedge \boldsymbol{U} = 0,}\\
{\boldsymbol{\nabla } \wedge \boldsymbol{U} = \boldsymbol{\varOmega}
,\;\textrm{and}\;\textrm{so,}\;\zeta \,\boldsymbol{\varOmega} +
\boldsymbol{\nabla }\zeta \wedge \boldsymbol{U} = 0,}
\end{array}}
\right\}\end{equation}hence
![]() $\langle \boldsymbol{U},\boldsymbol{\varOmega} \rangle = 0$ and in the Serret–Frenet basis,
$\langle \boldsymbol{U},\boldsymbol{\varOmega} \rangle = 0$ and in the Serret–Frenet basis, ![]() $\boldsymbol{U} = \{ U,0,0\} $ and
$\boldsymbol{U} = \{ U,0,0\} $ and ![]() $\boldsymbol{\varOmega} = \{ 0,0,{\varOmega ^3}\} $, therefore
$\boldsymbol{\varOmega} = \{ 0,0,{\varOmega ^3}\} $, therefore ![]() $\boldsymbol{\nabla }\,\textrm{ln}\,\zeta $ is aligned with the principal normal
$\boldsymbol{\nabla }\,\textrm{ln}\,\zeta $ is aligned with the principal normal ![]() ${\boldsymbol{e}^2}$ direction (see figure 2) so that
${\boldsymbol{e}^2}$ direction (see figure 2) so that ![]() $\boldsymbol{\nabla }\,\textrm{ln}\,\zeta$ has components
$\boldsymbol{\nabla }\,\textrm{ln}\,\zeta$ has components
In the Serret–Frenet basis, ![]() $\boldsymbol{\varOmega} = \{ 0,0,{\varOmega ^3}\} = \{ 0,0,(U/R - {\partial _2}U)\} $ and
$\boldsymbol{\varOmega} = \{ 0,0,{\varOmega ^3}\} = \{ 0,0,(U/R - {\partial _2}U)\} $ and ![]() $\boldsymbol{\nabla }\,\textrm{ln}\,\zeta \wedge \boldsymbol{U} = \{ 0,0, - (U{\partial _2}\,\textrm{ln}\,\zeta )\}$.
$\boldsymbol{\nabla }\,\textrm{ln}\,\zeta \wedge \boldsymbol{U} = \{ 0,0, - (U{\partial _2}\,\textrm{ln}\,\zeta )\}$.
So we can write
An equivalent expression for ![]() $\zeta $ was obtained in the 2-D case described in F83 and we shall find that we will not have to solve (5.8) explicitly.
$\zeta $ was obtained in the 2-D case described in F83 and we shall find that we will not have to solve (5.8) explicitly.
5.2.2. Metric tensor and Christoffel symbols
We are now in a position to define the metric tensor for the transformation from Cartesian ![]() ${y^i}$ coordinates to the true streamline
${y^i}$ coordinates to the true streamline ![]() ${x^i} = \{ \phi ,g,f\} $ system. The contravariant metric tensor can be constructed directly from the products of the base vectors (Aris Reference Aris1962)
${x^i} = \{ \phi ,g,f\} $ system. The contravariant metric tensor can be constructed directly from the products of the base vectors (Aris Reference Aris1962)
 \begin{equation}{g^{pq}} = \sum\limits_i {\frac{{\partial {x^p}}}{{\partial {y^i}}}\frac{{\partial {x^q}}}{{\partial {y^i}}}} = \left( {\begin{array}{@{}ccc@{}} {{\zeta^2}{Q^2}}&0&0\\ 0&Q&0\\ 0&0&Q \end{array}} \right).\end{equation}
\begin{equation}{g^{pq}} = \sum\limits_i {\frac{{\partial {x^p}}}{{\partial {y^i}}}\frac{{\partial {x^q}}}{{\partial {y^i}}}} = \left( {\begin{array}{@{}ccc@{}} {{\zeta^2}{Q^2}}&0&0\\ 0&Q&0\\ 0&0&Q \end{array}} \right).\end{equation}
And, since the ![]() ${x^i}$ system is orthogonal, the covariant metric is
${x^i}$ system is orthogonal, the covariant metric is
 \begin{equation}{g_{pq}} = {({g^{pq}})^{ - 1}} = \sum\limits_i {\frac{{\partial {x^p}}}{{\partial {y^i}}}\frac{{\partial {x^q}}}{{\partial {y^i}}}} = \left( {\begin{array}{@{}ccc@{}} {\dfrac{1}{{{\zeta^2}{Q^2}}}}&0&0\\ 0&{\dfrac{1}{Q}}&0\\ 0&0&{\dfrac{1}{Q}} \end{array}} \right).\end{equation}
\begin{equation}{g_{pq}} = {({g^{pq}})^{ - 1}} = \sum\limits_i {\frac{{\partial {x^p}}}{{\partial {y^i}}}\frac{{\partial {x^q}}}{{\partial {y^i}}}} = \left( {\begin{array}{@{}ccc@{}} {\dfrac{1}{{{\zeta^2}{Q^2}}}}&0&0\\ 0&{\dfrac{1}{Q}}&0\\ 0&0&{\dfrac{1}{Q}} \end{array}} \right).\end{equation}
And we have written ![]() $Q = |U |$ to avoid confusion when using terms derived from the metric to perform steps in the coordinate transformation. It is worth noting that the metric takes a somewhat different form from that used in the 2-D streamline coordinates in F83. In that case the contravariant metric took the form
$Q = |U |$ to avoid confusion when using terms derived from the metric to perform steps in the coordinate transformation. It is worth noting that the metric takes a somewhat different form from that used in the 2-D streamline coordinates in F83. In that case the contravariant metric took the form
 \begin{equation}{g^{pq}} = \left( {\begin{array}{@{}ccc@{}} {{\zeta^2}{Q^2}}&0&0\\ 0&{{Q^2}}&0\\ 0&0&1 \end{array}} \right),\end{equation}
\begin{equation}{g^{pq}} = \left( {\begin{array}{@{}ccc@{}} {{\zeta^2}{Q^2}}&0&0\\ 0&{{Q^2}}&0\\ 0&0&1 \end{array}} \right),\end{equation}
the difference arising from the fact that in the 2-D case, the Lagrange streamfunction has dimensions ![]() ${L^2}/T$, whereas in the present 3-D case, the f and g streamfunctions each have dimensions
${L^2}/T$, whereas in the present 3-D case, the f and g streamfunctions each have dimensions ![]() ${({L^2}/T)^{1/2}}$. The modified potential function
${({L^2}/T)^{1/2}}$. The modified potential function ![]() $\phi $, however, has the same dimensions in both two and three dimensions.
$\phi $, however, has the same dimensions in both two and three dimensions.
The Jacobian of the transform is denoted by J and given by
So that the transformation is not invertable at stagnation points and solid surfaces, where the no-slip condition ensures ![]() $Q \to 0$. Finally, to effect the transformation we need to define the Christoffel symbols for the metric. These are the counterparts of the connection coefficients defined in (3.3) but since in the true
$Q \to 0$. Finally, to effect the transformation we need to define the Christoffel symbols for the metric. These are the counterparts of the connection coefficients defined in (3.3) but since in the true ![]() ${x^i} = \{ \phi ,g,f\} $ coordinate system, the base vectors can change their magnitude as well as their orientation as we move along coordinate lines, the simplifications we were able to use in the case of the orthonormal Serret–Frenet
${x^i} = \{ \phi ,g,f\} $ coordinate system, the base vectors can change their magnitude as well as their orientation as we move along coordinate lines, the simplifications we were able to use in the case of the orthonormal Serret–Frenet ![]() ${\boldsymbol{e}_i}$ basis are not available. The Christoffel symbols (of the second kind) are defined as (Aris Reference Aris1962)
${\boldsymbol{e}_i}$ basis are not available. The Christoffel symbols (of the second kind) are defined as (Aris Reference Aris1962)
The ![]() $\hat{\varGamma }_{jk}^i$ values for the
$\hat{\varGamma }_{jk}^i$ values for the ![]() ${x^i} = \{ \phi ,g,f\} $ metric (5.9), (5.10) are listed in Appendix C. If we now define
${x^i} = \{ \phi ,g,f\} $ metric (5.9), (5.10) are listed in Appendix C. If we now define ![]() $a,_{j}^i$, the covariant derivative in the
$a,_{j}^i$, the covariant derivative in the ![]() ${x^j}$ direction of a vector
${x^j}$ direction of a vector ![]() $\boldsymbol{a}$ with components
$\boldsymbol{a}$ with components ![]() ${a^i}$ in the
${a^i}$ in the ![]() ${x^i}$ system, as
${x^i}$ system, as
we are now in a position to transform flow equations from Cartesian ![]() ${y^i}$ coordinates to
${y^i}$ coordinates to ![]() ${x^i} = \{ \phi ,g,f\} $ coordinates. The procedure is as follows.
${x^i} = \{ \phi ,g,f\} $ coordinates. The procedure is as follows.
(i) Write down the original equation in Cartesian form.
(ii) Rewrite the equation in general tensor form, replacing partial derivatives by covariant derivatives and ensuring all terms have the same variance.
(iii) Substitute for the covariant derivatives using (5.14) and (5.13).
(iv) Recover physical components.
These steps were set out in Bradshaw (Reference Bradshaw1973, Appendix I) and can be followed in detail in the 2-D case in F83.
5.2.3. Connection coefficients for the Serret–Frenet basis
We are ultimately interested in step (iv), so in the present case, rather than go through steps (i)–(iii), we will simply normalise the Christoffel symbols ![]() $\hat{\varGamma }_{jk}^i$ to recover the equivalent connection coefficients
$\hat{\varGamma }_{jk}^i$ to recover the equivalent connection coefficients ![]() $\varGamma _{jk}^i$ of the orthonormal Serret–Frenet
$\varGamma _{jk}^i$ of the orthonormal Serret–Frenet ![]() ${\boldsymbol{e}_i}$ basis corresponding to the
${\boldsymbol{e}_i}$ basis corresponding to the ![]() ${x^i} = \{ \phi ,g,f\} $ system and substitute these in (3.4) with the form of the fluid stress tensor given in (3.7).
${x^i} = \{ \phi ,g,f\} $ system and substitute these in (3.4) with the form of the fluid stress tensor given in (3.7).
These nine connection coefficients are
 \begin{align}\left. {\begin{array}{@{}c@{}} {\varGamma_{22}^1 ={-} \varGamma_{12}^2 = 1/2{L_a},\quad \varGamma_{33}^1 ={-} \varGamma_{13}^3 = 1/2{L_a},\quad \varGamma_{11}^2 ={-} \varGamma_{21}^1 = 1/R,}\\ {\varGamma_{33}^2 ={-} \varGamma_{23}^3 = 1/2{L_{a2}},\quad \varGamma_{22}^3 ={-} \varGamma_{32}^2 = 1/2{L_{a3}},}\\ {\varGamma_{11}^3 ={-} \varGamma_{31}^1 = 0,\quad \varGamma_{23}^1 ={-} \varGamma_{13}^2 = 0,\quad \varGamma_{32}^1 ={-} \varGamma_{12}^3 = 0,\quad \varGamma_{21}^3 ={-} \varGamma_{31}^2 = 0,} \end{array}} \right\}\end{align}
\begin{align}\left. {\begin{array}{@{}c@{}} {\varGamma_{22}^1 ={-} \varGamma_{12}^2 = 1/2{L_a},\quad \varGamma_{33}^1 ={-} \varGamma_{13}^3 = 1/2{L_a},\quad \varGamma_{11}^2 ={-} \varGamma_{21}^1 = 1/R,}\\ {\varGamma_{33}^2 ={-} \varGamma_{23}^3 = 1/2{L_{a2}},\quad \varGamma_{22}^3 ={-} \varGamma_{32}^2 = 1/2{L_{a3}},}\\ {\varGamma_{11}^3 ={-} \varGamma_{31}^1 = 0,\quad \varGamma_{23}^1 ={-} \varGamma_{13}^2 = 0,\quad \varGamma_{32}^1 ={-} \varGamma_{12}^3 = 0,\quad \varGamma_{21}^3 ={-} \varGamma_{31}^2 = 0,} \end{array}} \right\}\end{align}where
and the streamline curvature ![]() $1/R$ is a signed quantity which is +ve (−ve) if the centre of curvature lies in the +ve (−ve)
$1/R$ is a signed quantity which is +ve (−ve) if the centre of curvature lies in the +ve (−ve) ![]() ${x^2}$ direction. Note that connection coefficients
${x^2}$ direction. Note that connection coefficients ![]() $\varGamma _{\beta \gamma }^\alpha $ with
$\varGamma _{\beta \gamma }^\alpha $ with ![]() $\alpha ,\;\beta ,\;\gamma $ all different are zero as non-zero values would indicate that the coordinate lines were twisted curves. In general 3-D complex-lamellar flows, the streamlines and their orthogonal trajectories are plane curves.
$\alpha ,\;\beta ,\;\gamma $ all different are zero as non-zero values would indicate that the coordinate lines were twisted curves. In general 3-D complex-lamellar flows, the streamlines and their orthogonal trajectories are plane curves.
5.3. Spatial geometry of the coordinates and base vectors
It is illuminating to make explicit the links between the geometry of the coordinate lines, the ![]() ${\boldsymbol{e}_i}$ basis and the variation of the mean velocity in space. In the 2-D case treated in F83, the streamline and the
${\boldsymbol{e}_i}$ basis and the variation of the mean velocity in space. In the 2-D case treated in F83, the streamline and the ![]() ${x^2}$coordinate line were both confined to the osculating plane and
${x^2}$coordinate line were both confined to the osculating plane and ![]() $(1/\hat{R})$, the curvature of the
$(1/\hat{R})$, the curvature of the ![]() ${x^2}$ line equalled
${x^2}$ line equalled ![]() $1/{L_a}$. In the present 3-D case, we can only assume that the principal normal and binormal to the
$1/{L_a}$. In the present 3-D case, we can only assume that the principal normal and binormal to the ![]() ${x^2}$ line lie in the tangent plane of the
${x^2}$ line lie in the tangent plane of the ![]() ${x^1}$ streamline, as we show in figure 3(a). If we denote the tangent, principal normal, binormal and curvature of the
${x^1}$ streamline, as we show in figure 3(a). If we denote the tangent, principal normal, binormal and curvature of the ![]() ${x^2}$ line as
${x^2}$ line as ![]() ${\hat{\boldsymbol{e}}_1}$,
${\hat{\boldsymbol{e}}_1}$, ![]() ${\hat{\boldsymbol{e}}_2}$,
${\hat{\boldsymbol{e}}_2}$, ![]() ${\hat{\boldsymbol{e}}_3}$ and
${\hat{\boldsymbol{e}}_3}$ and ![]() $(1/\hat{R})$, respectively, and the angle between
$(1/\hat{R})$, respectively, and the angle between ![]() ${\hat{\boldsymbol{e}}_2}$ and
${\hat{\boldsymbol{e}}_2}$ and ![]() ${\boldsymbol{e}_1}$ as
${\boldsymbol{e}_1}$ as ![]() $\theta $, it follows from the Serret–Frenet relationships (2.4) and from the definitions of the connection coefficients (5.15) that
$\theta $, it follows from the Serret–Frenet relationships (2.4) and from the definitions of the connection coefficients (5.15) that

Figure 3. (a) Curvature of ![]() ${x^2}$ coordinate line relative to the base vectors
${x^2}$ coordinate line relative to the base vectors ![]() ${\boldsymbol{e}_i}$. (b) Curvature of
${\boldsymbol{e}_i}$. (b) Curvature of ![]() ${x^3}$ coordinate line relative to the base vectors
${x^3}$ coordinate line relative to the base vectors ![]() ${\boldsymbol{e}_i}$.
${\boldsymbol{e}_i}$.
Similarly, we can only assume that the principal normal and binormal to the ![]() ${x^3}$ line lie in the osculating plane of the
${x^3}$ line lie in the osculating plane of the ![]() ${x^1}$ streamline (figure 3b). If we denote the tangent, principal normal, binormal and curvature of the
${x^1}$ streamline (figure 3b). If we denote the tangent, principal normal, binormal and curvature of the ![]() ${x^3}$ line as
${x^3}$ line as ![]() ${{\boldsymbol{\hat{e}}}_1}$,
${{\boldsymbol{\hat{e}}}_1}$, ![]() ${{\boldsymbol{\hat{e}}}_2}$,
${{\boldsymbol{\hat{e}}}_2}$, ![]() ${{\boldsymbol{\hat{e}}}_3}$ and
${{\boldsymbol{\hat{e}}}_3}$ and ![]() $(1/\hat{\hat{R}})$, respectively, and the angle between
$(1/\hat{\hat{R}})$, respectively, and the angle between ![]() ${{\boldsymbol{\hat{e}}}_2}$ and
${{\boldsymbol{\hat{e}}}_2}$ and ![]() ${\boldsymbol{e}_1}$ as
${\boldsymbol{e}_1}$ as ![]() $\phi $, it follows from the Serret–Frenet relationships and from the definitions of the connection coefficients that
$\phi $, it follows from the Serret–Frenet relationships and from the definitions of the connection coefficients that
Hence, the spatial geometry of the ![]() ${x^2}$ and
${x^2}$ and ![]() ${x^3}$ coordinate lines is completely determined by the e-folding distances of the mean velocity in the streamwise and cross-stream directions.
${x^3}$ coordinate lines is completely determined by the e-folding distances of the mean velocity in the streamwise and cross-stream directions.
Finally, we point out that, since we have orientated the basis by identifying the ![]() ${\boldsymbol{e}_i}$ tangent planes with the tangent planes to the surface, the surface streamlines are curves whose principal normals are always normal to the surface and so are geodesics.
${\boldsymbol{e}_i}$ tangent planes with the tangent planes to the surface, the surface streamlines are curves whose principal normals are always normal to the surface and so are geodesics.
5.4. Physical momentum equations in three-dimensional complex-lamellar flow
Substituting (5.15), (5.16) and (3.7) into (3.4) we obtain the momentum equations
 \begin{align}
U{\partial _1}U & = \dfrac{{{U^2}}}{{{L_a}}} ={-} {\partial
_1}P - {\partial _1}\overline {{u^1}{u^1}} - {\partial
_2}\overline {{u^1}{u^2}} - {\partial _3}\overline
{{u^1}{u^3}} \nonumber\\
& \quad + \overline {{u^1}{u^1}}
\dfrac{1}{{{L_a}}} - \overline {{u^2}{u^2}}
\dfrac{1}{{2{L_a}}} - \overline {{u^3}{u^3}}
\dfrac{1}{{2{L_a}}} + \overline {{u^1}{u^2}} \left(
{\dfrac{2}{R} + \dfrac{1}{{2{L_{a2}}}}} \right) + \overline
{{u^1}{u^3}} \dfrac{1}{{2{L_{a3}}}}\nonumber\\
& \quad + \nu \left[
{\partial_1}({\partial_1}U) + {\partial_2}({\partial_2}U)
+ {\partial_3}({\partial_3}U) -
\dfrac{3}{{2{L_a}}}({\partial_1}U)\right.\nonumber\\
&\quad -\left. \left( {\dfrac{2}{R} +
\dfrac{1}{{2{L_{a2}}}}} \right)({\partial_2}U) -
\dfrac{1}{{2{L_{a3}}}}({\partial_3}U) \right] + F_D^1,
\end{align}
\begin{align}
U{\partial _1}U & = \dfrac{{{U^2}}}{{{L_a}}} ={-} {\partial
_1}P - {\partial _1}\overline {{u^1}{u^1}} - {\partial
_2}\overline {{u^1}{u^2}} - {\partial _3}\overline
{{u^1}{u^3}} \nonumber\\
& \quad + \overline {{u^1}{u^1}}
\dfrac{1}{{{L_a}}} - \overline {{u^2}{u^2}}
\dfrac{1}{{2{L_a}}} - \overline {{u^3}{u^3}}
\dfrac{1}{{2{L_a}}} + \overline {{u^1}{u^2}} \left(
{\dfrac{2}{R} + \dfrac{1}{{2{L_{a2}}}}} \right) + \overline
{{u^1}{u^3}} \dfrac{1}{{2{L_{a3}}}}\nonumber\\
& \quad + \nu \left[
{\partial_1}({\partial_1}U) + {\partial_2}({\partial_2}U)
+ {\partial_3}({\partial_3}U) -
\dfrac{3}{{2{L_a}}}({\partial_1}U)\right.\nonumber\\
&\quad -\left. \left( {\dfrac{2}{R} +
\dfrac{1}{{2{L_{a2}}}}} \right)({\partial_2}U) -
\dfrac{1}{{2{L_{a3}}}}({\partial_3}U) \right] + F_D^1,
\end{align} \begin{align}\dfrac{{{U^2}}}{R} & ={-} {\partial _2}P - {\partial_1}\overline {{u^1}{u^2}} - {\partial _2}\overline{{u^2}{u^2}} - {\partial _3}\overline {{u^2}{u^3}} \nonumber\\ & \quad - (\overline {{u^1}{u^1}} - \overline {{u^2}{u^2}})\dfrac{1}{R} - (\overline {{u^3}{u^3}} - \overline{{u^2}{u^2}} )\dfrac{1}{{2{L_a}_2}} + \overline{{u^1}{u^2}} \dfrac{3}{{2{L_a}}} + \overline {{u^2}{u^3}} \dfrac{1}{{2{L_a}_3}}\nonumber\\ & \quad + \nu \left[ {{\partial_1}({\partial_2}U) - \dfrac{1}{2}{\partial_2}({\partial_1}U) + {\partial_3}({\partial_3}U) + {\partial_1}U\dfrac{3}{{2R}} - {\partial_2}U\dfrac{3}{{2{L_a}}} - {\partial_3}U\dfrac{1}{{{L_{a3}}}}} \right] + F_D^2, \end{align}
\begin{align}\dfrac{{{U^2}}}{R} & ={-} {\partial _2}P - {\partial_1}\overline {{u^1}{u^2}} - {\partial _2}\overline{{u^2}{u^2}} - {\partial _3}\overline {{u^2}{u^3}} \nonumber\\ & \quad - (\overline {{u^1}{u^1}} - \overline {{u^2}{u^2}})\dfrac{1}{R} - (\overline {{u^3}{u^3}} - \overline{{u^2}{u^2}} )\dfrac{1}{{2{L_a}_2}} + \overline{{u^1}{u^2}} \dfrac{3}{{2{L_a}}} + \overline {{u^2}{u^3}} \dfrac{1}{{2{L_a}_3}}\nonumber\\ & \quad + \nu \left[ {{\partial_1}({\partial_2}U) - \dfrac{1}{2}{\partial_2}({\partial_1}U) + {\partial_3}({\partial_3}U) + {\partial_1}U\dfrac{3}{{2R}} - {\partial_2}U\dfrac{3}{{2{L_a}}} - {\partial_3}U\dfrac{1}{{{L_{a3}}}}} \right] + F_D^2, \end{align} \begin{align}0 & ={-} {\partial _3}P - {\partial _1}\overline {{u^1}{u^3}} - {\partial _2}\overline {{u^2}{u^3}} - {\partial_3}\overline {{u^3}{u^3}} \nonumber\\ & \quad - (\overline {{u^2}{u^2}} - \overline {{u^3}{u^3}})\dfrac{1}{{2{L_{a3}}}} + \overline {{u^1}{u^3}} \dfrac{3}{{2{L_a}}} - \overline {{u^2}{u^3}} \left({2\varGamma_{23}^3 - \dfrac{1}{R}} \right)\nonumber\\ & \quad + \nu \left[ {{\partial_1}({\partial_3}U) + {\partial_2}({\partial_3}U) - \dfrac{1}{2}{\partial_3}({\partial_1}U) - ({\partial_3}U)\left( {\dfrac{3}{{2{L_a}}} + \dfrac{1}{R} + \dfrac{1}{{{L_{a2}}}}} \right)} \right] + F_D^3. \end{align}
\begin{align}0 & ={-} {\partial _3}P - {\partial _1}\overline {{u^1}{u^3}} - {\partial _2}\overline {{u^2}{u^3}} - {\partial_3}\overline {{u^3}{u^3}} \nonumber\\ & \quad - (\overline {{u^2}{u^2}} - \overline {{u^3}{u^3}})\dfrac{1}{{2{L_{a3}}}} + \overline {{u^1}{u^3}} \dfrac{3}{{2{L_a}}} - \overline {{u^2}{u^3}} \left({2\varGamma_{23}^3 - \dfrac{1}{R}} \right)\nonumber\\ & \quad + \nu \left[ {{\partial_1}({\partial_3}U) + {\partial_2}({\partial_3}U) - \dfrac{1}{2}{\partial_3}({\partial_1}U) - ({\partial_3}U)\left( {\dfrac{3}{{2{L_a}}} + \dfrac{1}{R} + \dfrac{1}{{{L_{a2}}}}} \right)} \right] + F_D^3. \end{align}
Before discussing these equations in more detail in § 6, we can make the following comments: the asymmetry of the connection coefficients, which results from the asymmetry in the variation of the base vectors along their integral curves as set out in the Serret–Frenet equations (2.4), together with the fact that we have orientated the ![]() ${\boldsymbol{e}_i}$ basis by identifying its tangent planes with those of the surface, means that the coordinate indices
${\boldsymbol{e}_i}$ basis by identifying its tangent planes with those of the surface, means that the coordinate indices ![]() ${x^1},\;{x^2},\;{x^3}$ cannot be simply interchanged.
${x^1},\;{x^2},\;{x^3}$ cannot be simply interchanged. ![]() ${\boldsymbol{e}_2}$ and
${\boldsymbol{e}_2}$ and ![]() ${x^2}$ must intersect the surface normally and
${x^2}$ must intersect the surface normally and ![]() ${\boldsymbol{e}_i}$ is taken as a right-handed triad. If the meteorological convention with
${\boldsymbol{e}_i}$ is taken as a right-handed triad. If the meteorological convention with ![]() ${\boldsymbol{e}_3},\;{x^3}$ normal to the surface is preferred, then
${\boldsymbol{e}_3},\;{x^3}$ normal to the surface is preferred, then ![]() ${\boldsymbol{e}_i}$ should be treated as left handed and appropriate changes made to the sign conventions. This lack of symmetry in the vector basis leads to a corresponding lack of symmetry in the elements of the stress tensor divergence, which is particularly noticeable in the viscous terms.
${\boldsymbol{e}_i}$ should be treated as left handed and appropriate changes made to the sign conventions. This lack of symmetry in the vector basis leads to a corresponding lack of symmetry in the elements of the stress tensor divergence, which is particularly noticeable in the viscous terms.
As noted in (4.10) et seq, the directional derivatives ![]() ${\partial _i}({\partial _j})$ do not commute so that the order of second derivatives in the flow equations cannot be altered arbitrarily. Expressions for the non-commutivity of directional derivatives of an arbitrary vector are given in Appendix A.
${\partial _i}({\partial _j})$ do not commute so that the order of second derivatives in the flow equations cannot be altered arbitrarily. Expressions for the non-commutivity of directional derivatives of an arbitrary vector are given in Appendix A.
Finally, the 3-D momentum equations have, in principle, four unknowns, U, P, ![]() $(1/R)$,
$(1/R)$, ![]() $(1/\sigma )$. The pair of 2-D equations presented in § 1 had three unknowns, U, P,
$(1/\sigma )$. The pair of 2-D equations presented in § 1 had three unknowns, U, P, ![]() $(1/R)$ and the equation set had to be closed by use of a structure equation (2.3). In the 3-D complex-lamellar case we have stipulated that
$(1/R)$ and the equation set had to be closed by use of a structure equation (2.3). In the 3-D complex-lamellar case we have stipulated that ![]() $(1/\sigma ) = 0$, which plays the role of a structure equation, hence one variable has disappeared and the three momentum equations are closed.
$(1/\sigma ) = 0$, which plays the role of a structure equation, hence one variable has disappeared and the three momentum equations are closed.
6. Scalar conservation equations
Since one of the original motivations for this work was understanding the transport of scalars in atmospheric flow over complex terrain, it is appropriate to add the equation for conservation of an arbitrary scalar ![]() $C({\kern0.9pt}\boldsymbol{y})$ in the physical complex-lamellar system,
$C({\kern0.9pt}\boldsymbol{y})$ in the physical complex-lamellar system, ![]() ${x^i},\;{\boldsymbol{e}_i}$. The flux of C is given by
${x^i},\;{\boldsymbol{e}_i}$. The flux of C is given by
where c is the turbulent fluctuation of the scalar around its mean value C and ![]() ${\kappa _c}$ is the coefficient of molecular diffusion of C. Then, from the expression for the divergence of a vector in Appendix A and using the values for the connection coefficients
${\kappa _c}$ is the coefficient of molecular diffusion of C. Then, from the expression for the divergence of a vector in Appendix A and using the values for the connection coefficients ![]() $\varGamma _{jk}^i$ given in (5.15), we obtain
$\varGamma _{jk}^i$ given in (5.15), we obtain
 \begin{align} U{\partial _1}C &={-} {\partial _1}\overline {{u^1}c} -{\partial _2}\overline {{u^2}c} - {\partial _3}\overline{{u^3}c} + \dfrac{{\overline {{u^1}c} }}{{{L_a}}} + \overline {{u^2}c} \left( {\dfrac{1}{{2{L_{a2}}}} + \dfrac{1}{R}} \right) + \dfrac{{\overline {{u^3}c}}}{{2{L_{a3}}}}\nonumber\\ & \quad + {\kappa _c}\left[{{\partial_1}({\partial_1}C) + {\partial_2}{{({\partial_2}C)}} + {\partial_3}({\partial_3}C) - \dfrac{{{\partial_1}C}}{{{L_a}}} - \dfrac{{{\partial_2}C}}{{2{L_{a2}}}} - \dfrac{{{\partial_2}C}}{R} - \dfrac{{{\partial_3}C}}{{2{L_{a3}}}}} \right] + {\chi _C}, \end{align}
\begin{align} U{\partial _1}C &={-} {\partial _1}\overline {{u^1}c} -{\partial _2}\overline {{u^2}c} - {\partial _3}\overline{{u^3}c} + \dfrac{{\overline {{u^1}c} }}{{{L_a}}} + \overline {{u^2}c} \left( {\dfrac{1}{{2{L_{a2}}}} + \dfrac{1}{R}} \right) + \dfrac{{\overline {{u^3}c}}}{{2{L_{a3}}}}\nonumber\\ & \quad + {\kappa _c}\left[{{\partial_1}({\partial_1}C) + {\partial_2}{{({\partial_2}C)}} + {\partial_3}({\partial_3}C) - \dfrac{{{\partial_1}C}}{{{L_a}}} - \dfrac{{{\partial_2}C}}{{2{L_{a2}}}} - \dfrac{{{\partial_2}C}}{R} - \dfrac{{{\partial_3}C}}{{2{L_{a3}}}}} \right] + {\chi _C}, \end{align}
where ![]() ${\chi _C}$ is the source strength of C. As in the case of the momentum equations, the advection term is simplified to advection along the streamline at the expense of extra terms related to the distortion of an infinitesimal control volume as streamlines curve, converge and diverge.
${\chi _C}$ is the source strength of C. As in the case of the momentum equations, the advection term is simplified to advection along the streamline at the expense of extra terms related to the distortion of an infinitesimal control volume as streamlines curve, converge and diverge.
7. Summary and discussion
7.1. General three-dimensional flow fields
We have attempted to extend the 2-D physical streamline coordinate equations derived in F83 to three dimensions. This exercise devolves to defining the nine non-zero connection coefficients of an orthonormal moving frame, consisting of the Serret–Frenet basis, ![]() ${\boldsymbol{e}_i}$, in terms of the mean flow field
${\boldsymbol{e}_i}$, in terms of the mean flow field ![]() $\boldsymbol{U}(\boldsymbol{x})$ so that the coordinate system itself is supplied by the solution of the equations. The connection coefficients
$\boldsymbol{U}(\boldsymbol{x})$ so that the coordinate system itself is supplied by the solution of the equations. The connection coefficients ![]() $\varGamma _{jk}^i$ are the components of the derivatives of
$\varGamma _{jk}^i$ are the components of the derivatives of ![]() ${\boldsymbol{e}_i}$ along their integral curves
${\boldsymbol{e}_i}$ along their integral curves ![]() ${x^i}$. We found that, if the mean flow has a component of its vorticity aligned in the streamwise direction, i.e. if
${x^i}$. We found that, if the mean flow has a component of its vorticity aligned in the streamwise direction, i.e. if ![]() $\langle \boldsymbol{U},\boldsymbol{\varOmega} \rangle \ne 0$, its streamlines are twisted curves the so that
$\langle \boldsymbol{U},\boldsymbol{\varOmega} \rangle \ne 0$, its streamlines are twisted curves the so that ![]() ${\boldsymbol{e}_i}$ basis is not orientable. Furthermore, by applying the vector form of the Frobenius integral theorem to the field of
${\boldsymbol{e}_i}$ basis is not orientable. Furthermore, by applying the vector form of the Frobenius integral theorem to the field of ![]() ${\boldsymbol{e}_i}$ vectors, we deduced that the congruence of streamlines passing through any space curve does not constitute an integrable manifold. As a result, it is not possible to solve the ‘structure equations’, which define the connection coefficients, by analytic means. These two properties mean that it is not possible to write physical streamline coordinate equations for completely general flow fields but, conversely, in complex-lamellar flows, where
${\boldsymbol{e}_i}$ vectors, we deduced that the congruence of streamlines passing through any space curve does not constitute an integrable manifold. As a result, it is not possible to solve the ‘structure equations’, which define the connection coefficients, by analytic means. These two properties mean that it is not possible to write physical streamline coordinate equations for completely general flow fields but, conversely, in complex-lamellar flows, where ![]() ${\langle \boldsymbol{U},\boldsymbol{\varOmega} \rangle = 0}$, these obstacles disappear and the extension of the 2-D case to three dimensions is possible.
${\langle \boldsymbol{U},\boldsymbol{\varOmega} \rangle = 0}$, these obstacles disappear and the extension of the 2-D case to three dimensions is possible.
Remaining with general flows for the moment, it is possible to write the flow equations in the Serret–Frenet moving frame although not all the connection coefficients can be defined. The form of the resulting momentum equations shows that all the information about the linear momentum of the flow is contained in the streamwise, ![]() ${x^1},\;{\boldsymbol{e}_1}$ equation, where the streamwise mean pressure gradient is balanced by the inertial acceleration along the streamline plus the streamwise components of the fluid stress divergence and body force. Similarly, all the information about the angular momentum of the flow is contained in the principal normal,
${x^1},\;{\boldsymbol{e}_1}$ equation, where the streamwise mean pressure gradient is balanced by the inertial acceleration along the streamline plus the streamwise components of the fluid stress divergence and body force. Similarly, all the information about the angular momentum of the flow is contained in the principal normal, ![]() ${x^2},\;{\boldsymbol{e}_2}$ equation, where the mean pressure gradient in the cross-stream
${x^2},\;{\boldsymbol{e}_2}$ equation, where the mean pressure gradient in the cross-stream ![]() ${\boldsymbol{e}_2}$ direction is balanced by the centrifugal acceleration plus the
${\boldsymbol{e}_2}$ direction is balanced by the centrifugal acceleration plus the ![]() ${\boldsymbol{e}_2}$ components of the fluid stress divergence and body force. There is no other kind of momentum so any mean pressure gradient in the
${\boldsymbol{e}_2}$ components of the fluid stress divergence and body force. There is no other kind of momentum so any mean pressure gradient in the ![]() ${x^3},\;{\boldsymbol{e}_3}$ or binormal direction can only be produced by fluid stress divergence or a body force. In inviscid non-turbulent fluids in the absence of body forces, there can be no mean pressure gradient in the binormal direction. This seems a slightly surprising result but consideration of simple flows such as those around a body of revolution shows that this condition is generally observed.
${x^3},\;{\boldsymbol{e}_3}$ or binormal direction can only be produced by fluid stress divergence or a body force. In inviscid non-turbulent fluids in the absence of body forces, there can be no mean pressure gradient in the binormal direction. This seems a slightly surprising result but consideration of simple flows such as those around a body of revolution shows that this condition is generally observed.
Finnigan (Reference Finnigan1990) investigated the consequences of the non-integrability of stream surfaces in general 3-D flow fields in more detail and showed that there were regions where combinations of values of ![]() $1/{L_a},A,{A_n}$ and
$1/{L_a},A,{A_n}$ and ![]() ${A_b}$ would lead the streamlines to exhibit chaotic trajectories with possible enhancement of mixing through Lagrangian turbulence.
${A_b}$ would lead the streamlines to exhibit chaotic trajectories with possible enhancement of mixing through Lagrangian turbulence.
7.2. Complex-lamellar flows in three dimensions
Turning our attention to general complex-lamellar flows, it can be shown that they are a good approximation to boundary layers and free shear layers, which vary much more slowly in the streamwise than in the cross-stream directions. We first constructed a true coordinate system for these flows by deriving the functional form of two stream surfaces, ![]() $f,\;g$ and a modified potential surface,
$f,\;g$ and a modified potential surface, ![]() $\phi $, which together formed a normal congruence of surfaces, a condition that is a general property of complex-lamellar flows. The intersections of the surfaces define the streamline and two orthogonal trajectories, which can be taken as the coordinate axes. Distance along the axes is measured by the change in the value of the particular
$\phi $, which together formed a normal congruence of surfaces, a condition that is a general property of complex-lamellar flows. The intersections of the surfaces define the streamline and two orthogonal trajectories, which can be taken as the coordinate axes. Distance along the axes is measured by the change in the value of the particular ![]() $\phi ,\;f$ or g that the axes intersect normally and differentiation along any coordinate is automatically partial differentiation as only one of
$\phi ,\;f$ or g that the axes intersect normally and differentiation along any coordinate is automatically partial differentiation as only one of ![]() $\phi ,\;f,\;g$ varies along their intersections. In principal, flow equations in this true system could be solved by standard methods so we have supplied the metric of the transform from Cartesian coordinates and the relevant Christoffel symbols but have not followed all the necessary steps in the derivation. These can be followed in detail in F83 or Bradshaw (Reference Bradshaw1973).
$\phi ,\;f,\;g$ varies along their intersections. In principal, flow equations in this true system could be solved by standard methods so we have supplied the metric of the transform from Cartesian coordinates and the relevant Christoffel symbols but have not followed all the necessary steps in the derivation. These can be followed in detail in F83 or Bradshaw (Reference Bradshaw1973).
Instead, we deduced the form of the physical equations directly by normalising the Christoffel symbols and using general expressions for the gradient, divergence and curl of vectors and the divergence of second-order tensors in an orthonormal moving frame as explained above. This was equivalent to normalising the vector basis of the true coordinates to yield the Serret–Frenet basis and to measuring distance along the coordinate axes by physical distance. Variables in the resulting physical momentum and scalar conservation equations took the form they would have in Cartesian coordinates. The advection terms and dominant stress divergence terms are simplified but at the expense of the replacement of partial derivatives by directional derivatives and of extra terms that reflect the fact that the base vectors change orientation as they are convected along the streamline. As explained in § 5.1, we orientate the Serret–Frenet ![]() ${\boldsymbol{e}_i}$ basis by making its tangent planes tangent to the solid surface so that the principal normal
${\boldsymbol{e}_i}$ basis by making its tangent planes tangent to the solid surface so that the principal normal ![]() ${\boldsymbol{e}_2}$ vectors are normal to the surface and consequently, the surface streamlines are geodesics. The only component of mean vorticity is
${\boldsymbol{e}_2}$ vectors are normal to the surface and consequently, the surface streamlines are geodesics. The only component of mean vorticity is ![]() ${\varOmega ^3} = (U/R - {\partial _2}U)$ and the no-slip condition ensures that as
${\varOmega ^3} = (U/R - {\partial _2}U)$ and the no-slip condition ensures that as ![]() ${x^2} \to 0,\;{\varOmega ^3} \to - {\partial _2}U$.
${x^2} \to 0,\;{\varOmega ^3} \to - {\partial _2}U$.
7.3. Scaling the flow equations
When we make a set of rational approximations to the streamline momentum equations, discarding smaller terms and retaining larger, as is done in small-perturbation approaches to calculations (e.g. Van Dyke Reference Van Dyke1975; Hunt et al. Reference Hunt, Leibovich and Richards1988; Harman & Finnigan Reference Harman and Finnigan2010, Reference Harman and Finnigan2013), it is interesting to see that we arrive at a different place than if took the Cartesian or surface-following s-n equations as our starting point. As a practical example we will address the application of the streamline equations to an atmospheric boundary layer over gentle topography but the arguments apply equally to attached boundary layers over a non-planar surfaces or to thin free shear layers. We assume the ground surface is covered with bumps, undulations or hills with dimensions ![]() ${L_1},\;H,\;{L_3}$ in the streamwise
${L_1},\;H,\;{L_3}$ in the streamwise ![]() ${x^1}$, vertical
${x^1}$, vertical ![]() ${x^2}$ and lateral
${x^2}$ and lateral ![]() ${x^3}$ directions respectively with
${x^3}$ directions respectively with ![]() $H/{L_1},\;H/{L_3} \ll 1$. We also assume that the shear stress layer thickness
$H/{L_1},\;H/{L_3} \ll 1$. We also assume that the shear stress layer thickness ![]() $\delta $, defined as the region in which perturbations to the turbulent stresses affect perturbations to the mean flow at first order (Hunt et al. Reference Hunt, Leibovich and Richards1988) satisfies
$\delta $, defined as the region in which perturbations to the turbulent stresses affect perturbations to the mean flow at first order (Hunt et al. Reference Hunt, Leibovich and Richards1988) satisfies ![]() $\delta \ll {L_1}$ or, equivalently, that the mixing length
$\delta \ll {L_1}$ or, equivalently, that the mixing length ![]() $l = u^{\ast}/{\varOmega ^3} \ll {L_1}$, where
$l = u^{\ast}/{\varOmega ^3} \ll {L_1}$, where ![]() $u^{\ast}= \sqrt { - \overline {{u^1}{u^2}} } $ is the friction velocity. In the high Reynolds number turbulence of the atmospheric surface layer we can ignore the viscous in comparison with the turbulent stresses. We note also that these scaling assumptions are precisely those needed to approximate the flow as complex lamellar (see § 5.1).
$u^{\ast}= \sqrt { - \overline {{u^1}{u^2}} } $ is the friction velocity. In the high Reynolds number turbulence of the atmospheric surface layer we can ignore the viscous in comparison with the turbulent stresses. We note also that these scaling assumptions are precisely those needed to approximate the flow as complex lamellar (see § 5.1).
Focussing on the streamwise momentum equation (5.19) we observe four groups of terms. First, we have the mean inertia terms, ![]() $U{\partial _1}U = {U^2}/{L_a}$ and
$U{\partial _1}U = {U^2}/{L_a}$ and ![]() $- {\partial _1}P$ and we expect these to vary on the streamwise length scale
$- {\partial _1}P$ and we expect these to vary on the streamwise length scale ![]() ${L_1}$ because it is perturbations on this scale that generate perturbations in streamwise velocity and pressure gradient and so their magnitudes should scale as
${L_1}$ because it is perturbations on this scale that generate perturbations in streamwise velocity and pressure gradient and so their magnitudes should scale as ![]() $H/{L_1}$. Next, we have gradients of the shear and normal stresses
$H/{L_1}$. Next, we have gradients of the shear and normal stresses ![]() $- {\partial _1}\overline {{u^1}{u^1}} - {\partial _2}\overline {{u^1}{u^2}} - {\partial _3}\overline {{u^1}{u^3}}$. The second moments themselves are of order
$- {\partial _1}\overline {{u^1}{u^1}} - {\partial _2}\overline {{u^1}{u^2}} - {\partial _3}\overline {{u^1}{u^3}}$. The second moments themselves are of order ![]() $u^{\ast 2}$ and so smaller than
$u^{\ast 2}$ and so smaller than ![]() ${U^2}$ but in turbulent boundary layers over very rough surfaces, such as vegetation canopies,
${U^2}$ but in turbulent boundary layers over very rough surfaces, such as vegetation canopies, ![]() ${(u^{\ast 2}/{U^2})^{1/2}}$ can be as large as 0.3 (Raupach, Antonia & Rajagopalan Reference Raupach, Antonia and Rajagopalan1991). Since
${(u^{\ast 2}/{U^2})^{1/2}}$ can be as large as 0.3 (Raupach, Antonia & Rajagopalan Reference Raupach, Antonia and Rajagopalan1991). Since ![]() ${\partial _1} \sim 1/{L_1}$,
${\partial _1} \sim 1/{L_1}$, ![]() ${\partial _2} \sim 1/\delta$,
${\partial _2} \sim 1/\delta$, ![]() ${\partial _3} \sim 1/{L_3}$ in the shear stress layer
${\partial _3} \sim 1/{L_3}$ in the shear stress layer ![]() ${x^2} \le \delta $, the leading turbulent stress divergence term
${x^2} \le \delta $, the leading turbulent stress divergence term ![]() $- {\partial _2}\overline {{u^1}{u^2}}$ is comparable to the inertial terms. Next, we have a set of terms that are associated with the variation of the base vectors in space and which appear because the infinitesimal control volume
$- {\partial _2}\overline {{u^1}{u^2}}$ is comparable to the inertial terms. Next, we have a set of terms that are associated with the variation of the base vectors in space and which appear because the infinitesimal control volume ![]() $\textrm{d}\kern0.07em{x^1} \wedge \textrm{d}\kern0.07em{x^2} \wedge \textrm{d}\kern0.07em{x^3}$ changes its shape and orientation as it is advected along the streamline. These are the terms
$\textrm{d}\kern0.07em{x^1} \wedge \textrm{d}\kern0.07em{x^2} \wedge \textrm{d}\kern0.07em{x^3}$ changes its shape and orientation as it is advected along the streamline. These are the terms
and they all take the form of turbulent stresses multiplied by coefficients that describe the variation of the mean velocity in space. They involve ![]() $1/U{\partial _i}U$ the spatial variation of the logarithm of U and so are intrinsically smaller than the scale over which U itself varies, but in a free shear layer or boundary layer
$1/U{\partial _i}U$ the spatial variation of the logarithm of U and so are intrinsically smaller than the scale over which U itself varies, but in a free shear layer or boundary layer ![]() $1/{L_{a2}} \gg 1/{L_a}$,
$1/{L_{a2}} \gg 1/{L_a}$, ![]() $1/{L_{a3}}$ and so
$1/{L_{a3}}$ and so ![]() $\overline {{u^1}{u^2}} (1/2{L_{a2}})$ cannot be discarded a priori. Applying these arguments to (5.18), we can deduce that to
$\overline {{u^1}{u^2}} (1/2{L_{a2}})$ cannot be discarded a priori. Applying these arguments to (5.18), we can deduce that to ![]() $O[H/{L_1}]$ the dominant terms in a high Reynolds number turbulent boundary layer will be
$O[H/{L_1}]$ the dominant terms in a high Reynolds number turbulent boundary layer will be
and applying similar arguments to (5.19) and (5.20), the dominant terms will be
and
Finally, applying the same arguments to the scalar conservation equation (6.2), we obtain
In these small-perturbation equations we have retained the terms involving the eddy fluxes multiplied by ![]() $1/{L_{a2}}$ and
$1/{L_{a2}}$ and ![]() $1/R$. The first of these is because
$1/R$. The first of these is because ![]() $1/{L_{a2}}$ is intrinsically larger than
$1/{L_{a2}}$ is intrinsically larger than ![]() $1/{L_{a1}}$ and
$1/{L_{a1}}$ and ![]() $1/{L_{a3}}$. The second is because turbulent shear flows are particularly responsive to streamline curvature as we discuss next.
$1/{L_{a3}}$. The second is because turbulent shear flows are particularly responsive to streamline curvature as we discuss next.
We can estimate the size of ![]() $1/R$ by assuming the surface streamline over a bump or hill is an arc of a circle of radius R and chord
$1/R$ by assuming the surface streamline over a bump or hill is an arc of a circle of radius R and chord ![]() $2{L_1}$. Then by the chord theorem
$2{L_1}$. Then by the chord theorem ![]() $1/R \sim H/L_1^2$ so
$1/R \sim H/L_1^2$ so ![]() $1/R$ is much smaller than
$1/R$ is much smaller than ![]() $1/{L_1}$ so that on pure scaling grounds, curvature effects can only be significant if
$1/{L_1}$ so that on pure scaling grounds, curvature effects can only be significant if ![]() $(u^{\ast 2}/{U^2})(2U/R{\varOmega ^3}) \approx 1$, where
$(u^{\ast 2}/{U^2})(2U/R{\varOmega ^3}) \approx 1$, where ![]() $2U/R{\varOmega ^3}$ is the curvature Richardson number,
$2U/R{\varOmega ^3}$ is the curvature Richardson number, ![]() ${R_c}$. However,
${R_c}$. However, ![]() ${R_c}$ is a measure of the stability of a curved flow to small perturbations (Bradshaw Reference Bradshaw1969, Reference Bradshaw1973). It is the analogue of the buoyancy Richardson number in diabatically influenced flows. Positive
${R_c}$ is a measure of the stability of a curved flow to small perturbations (Bradshaw Reference Bradshaw1969, Reference Bradshaw1973). It is the analogue of the buoyancy Richardson number in diabatically influenced flows. Positive ![]() ${R_c}$ denotes a stable flow, which can supress turbulence over a hill crest and so helps promote separation behind a hill (Zeman & Jensen Reference Zeman and Jensen1987; Finnigan Reference Finnigan, Steffen and Denmead1988; Finnigan et al. Reference Finnigan, Raupach, Bradley and Aldis1990), while negative
${R_c}$ denotes a stable flow, which can supress turbulence over a hill crest and so helps promote separation behind a hill (Zeman & Jensen Reference Zeman and Jensen1987; Finnigan Reference Finnigan, Steffen and Denmead1988; Finnigan et al. Reference Finnigan, Raupach, Bradley and Aldis1990), while negative ![]() ${R_c}$ promotes the appearance of coherent streamwise vortices which augment turbulent transport of momentum to the surface. In the present 3-D case it is important to appreciate that this ‘stability’ effect is applied parallel to the
${R_c}$ promotes the appearance of coherent streamwise vortices which augment turbulent transport of momentum to the surface. In the present 3-D case it is important to appreciate that this ‘stability’ effect is applied parallel to the ![]() ${\boldsymbol{e}_2},\;{x^2}$ direction, not vertically, and so operates around the sides of any hills, with complicating effects on the turbulent stress divergence. Wind tunnel experiments by Harman and Finnigan (Reference Harman and Finnigan2021) on axisymmetric hills covered by a tall canopy and parallel large eddy simulations of those experiments by Patton, Sullivan & Weil (Reference Patton, Sullivan and Weil2022) illustrate these features and will be analysed in the framework presented here in forthcoming publications. Importantly, we deduce that, if the starting point for deriving small-perturbation approximations had been the momentum equations in surface-following coordinates (see Janour Reference Janour1975) or displaced Cartesian coordinates (see Hunt et al. Reference Hunt, Leibovich and Richards1988), then all the terms involving
${\boldsymbol{e}_2},\;{x^2}$ direction, not vertically, and so operates around the sides of any hills, with complicating effects on the turbulent stress divergence. Wind tunnel experiments by Harman and Finnigan (Reference Harman and Finnigan2021) on axisymmetric hills covered by a tall canopy and parallel large eddy simulations of those experiments by Patton, Sullivan & Weil (Reference Patton, Sullivan and Weil2022) illustrate these features and will be analysed in the framework presented here in forthcoming publications. Importantly, we deduce that, if the starting point for deriving small-perturbation approximations had been the momentum equations in surface-following coordinates (see Janour Reference Janour1975) or displaced Cartesian coordinates (see Hunt et al. Reference Hunt, Leibovich and Richards1988), then all the terms involving ![]() $1/{L_{a2}}$ and
$1/{L_{a2}}$ and ![]() $1/R$ would be absent. Furthemore, even if we did discard those terms so that the Cartesian and streamline equations took identical forms, ‘solutions’ to the the streamline equations would be located at different places over the topography than the Cartesian ‘solutions’. Hence, the solutions to small-perturbation models of flow over gentle topography derived from these several starting points can be significantly different.
$1/R$ would be absent. Furthemore, even if we did discard those terms so that the Cartesian and streamline equations took identical forms, ‘solutions’ to the the streamline equations would be located at different places over the topography than the Cartesian ‘solutions’. Hence, the solutions to small-perturbation models of flow over gentle topography derived from these several starting points can be significantly different.
7.4. Practical applications
We conclude with some comments on applying the 3-D theory to two practical cases. First, since one of the motivations for this work is the extension of small-perturbation analysis to flow over 3-D topography, we can ask how we parameterise and apply (7.2), (7.3) and (7.4) in such a case. Given topography defined by ![]() $Zs(\kern0.09em {y^1},{y^3}) = H\,f(\kern0.09em {y^1},{y^3})$ with H the hill height and
$Zs(\kern0.09em {y^1},{y^3}) = H\,f(\kern0.09em {y^1},{y^3})$ with H the hill height and ![]() $\boldsymbol{y} = \{ {y^1},{y^2},{y^3}\} $ the Cartesian reference frame, the first step is to compute an appropriate 3-D streamline coordinate frame. Following Belcher (Reference Belcher1990), Belcher et al. (Reference Belcher, Newley and Hunt1993) and Finnigan & Belcher (Reference Finnigan and Belcher2004) in the 2-D case, we can use as a vector basis the Frenet frame referred to the inviscid irrotational flow over
$\boldsymbol{y} = \{ {y^1},{y^2},{y^3}\} $ the Cartesian reference frame, the first step is to compute an appropriate 3-D streamline coordinate frame. Following Belcher (Reference Belcher1990), Belcher et al. (Reference Belcher, Newley and Hunt1993) and Finnigan & Belcher (Reference Finnigan and Belcher2004) in the 2-D case, we can use as a vector basis the Frenet frame referred to the inviscid irrotational flow over ![]() $Zs(\kern0.09em {y^1},{y^3})$. We obtain this by solving for the velociy field
$Zs(\kern0.09em {y^1},{y^3})$. We obtain this by solving for the velociy field ![]() $\boldsymbol{v}({\kern0.9pt}\boldsymbol{y})$ that satisfies
$\boldsymbol{v}({\kern0.9pt}\boldsymbol{y})$ that satisfies ![]() $\boldsymbol{v} = \boldsymbol{\nabla }\phi $ with
$\boldsymbol{v} = \boldsymbol{\nabla }\phi $ with ![]() ${\nabla ^2}\phi = 0$ and
${\nabla ^2}\phi = 0$ and ![]() $\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{n} = 0$ on the solid surface, with n the normal to the surface. For gentle topography, the boundary condition
$\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{n} = 0$ on the solid surface, with n the normal to the surface. For gentle topography, the boundary condition ![]() $\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{n} = 0$ can be applied on the plane
$\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{n} = 0$ can be applied on the plane ![]() $Zs = 0$ and analytic solutions easily obtained. For steeper topography, the
$Zs = 0$ and analytic solutions easily obtained. For steeper topography, the ![]() $\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{n} = 0$ condition must be applied on
$\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{n} = 0$ condition must be applied on ![]() $Zs(\kern0.09em {y^1},{y^3})$ and numerical methods are then required.
$Zs(\kern0.09em {y^1},{y^3})$ and numerical methods are then required.
We can assume that deviations of the actual flow from these potential flow coordinate lines are small except if separation occurs in the lee of the hill, see for example Kaimal & Finnigan (Reference Kaimal and Finnigan1994). In fact, the nonlinear parameterisation of the lower canopy layer in Finnigan & Belcher (Reference Finnigan, Ayotte, Harman, Katul, Oldroyd, Patton, Poggi, Ross and Taylor2004) does allow separation and reversed flow to occur in canopy in the lee of the hill but even in that region the potential flow coordinates still provide a useful reference frame. If we wish to obtain an analytical solution in the ‘small-perturbation, gentle topography’ case, then the only closure we can use to represent the turbulent stresses in terms of the mean flow is the first-order or ‘eddy diffusivity’ approach. Finnigan et al. (2015) have presented a detailed analysis of the use of first-order closure in complex canopy flows but their analysis is generally applicable, whether a canopy is present or not. In Cartesian coordinates, first-order closure takes the form
where ![]() $K({\kern0.9pt}\boldsymbol{y})$ is a position dependent scalar eddy diffusivity for momentum and the deviatoric part of the turbulent stress tensor
$K({\kern0.9pt}\boldsymbol{y})$ is a position dependent scalar eddy diffusivity for momentum and the deviatoric part of the turbulent stress tensor ![]() $\begin{array}{l} \overline {{u^i}{u^j}} \\ \end{array}$ is taken as proportional to the mean rate of strain tensor. To use (7.6) in the 3-D streamline system we rewrite it as
$\begin{array}{l} \overline {{u^i}{u^j}} \\ \end{array}$ is taken as proportional to the mean rate of strain tensor. To use (7.6) in the 3-D streamline system we rewrite it as
An equivalent slightly simpler formula relates the scalar eddy flux and the mean scalar gradient
The assumptions implicit in first-order closure are reasonably well satisfied in flow over topography up to the point of separation, at which point there is an abrupt change in the character of the flow and of the turbulence. In small-perturbation theories, upstream of the separation point, the eddy diffusivity is typically constructed using ![]() ${x^2}$, the distance from the surface, as a mixing length multiplied by some measure of the strength of the turbulent mixing such as the friction velocity of the undisturbed upwind flow, e.g. Hunt et al. (Reference Hunt, Leibovich and Richards1988), Finnigan & Belcher (Reference Finnigan and Belcher2004). Once the flow has separated, the scale of the turbulence is set by the size of the separation bubble rather than by
${x^2}$, the distance from the surface, as a mixing length multiplied by some measure of the strength of the turbulent mixing such as the friction velocity of the undisturbed upwind flow, e.g. Hunt et al. (Reference Hunt, Leibovich and Richards1988), Finnigan & Belcher (Reference Finnigan and Belcher2004). Once the flow has separated, the scale of the turbulence is set by the size of the separation bubble rather than by ![]() ${x^2}$ and first-order closure fails. In the absence of a general theory of turbulent flow separation, we turn to the empirical data on separation behind hills reviewed by Finnigan (Reference Finnigan, Steffen and Denmead1988) to anticipate when it should be expected. He found that steady separation bubbles usually appeared behind rough 2-D ridges with downwind slopes greater than 10°, while for 3-D axisymmetric hills the critical downstream angle was around 20°. In both cases the presence of a tall plant canopy caused separation to occur at lower angles. Behind hills steep enough or other objects bluff enough to have permanent separation regions, steady streamline coordinate theory can yield little insight into the flow. Nevertheless, the 3-D streamline system provided by the inviscid flow solution discussed above does give a useful reference frame linked to the geometry of the object.
${x^2}$ and first-order closure fails. In the absence of a general theory of turbulent flow separation, we turn to the empirical data on separation behind hills reviewed by Finnigan (Reference Finnigan, Steffen and Denmead1988) to anticipate when it should be expected. He found that steady separation bubbles usually appeared behind rough 2-D ridges with downwind slopes greater than 10°, while for 3-D axisymmetric hills the critical downstream angle was around 20°. In both cases the presence of a tall plant canopy caused separation to occur at lower angles. Behind hills steep enough or other objects bluff enough to have permanent separation regions, steady streamline coordinate theory can yield little insight into the flow. Nevertheless, the 3-D streamline system provided by the inviscid flow solution discussed above does give a useful reference frame linked to the geometry of the object.
The second main application we suggested for this theory was interpretation of data from field, wind tunnel or numerical experiments such as large eddy simulations of hill flows (e.g. Patton & Katul 2009). Experiments with sufficient data resolution to enable 3-D streamlines and consequently the ![]() ${x^i}$ coordinate lines to be accurately defined are now becoming available, mainly from wind tunnel simulations (Harman & Finnigan Reference Harman and Finnigan2021) and LES (Patton et al. Reference Patton, Sullivan and Weil2022). Analysis of these data in the streamline frame is ongoing. We believe it will provide new information on the sensitivity of the turbulent stresses to the flow distortion captured in the geometric parameters,
${x^i}$ coordinate lines to be accurately defined are now becoming available, mainly from wind tunnel simulations (Harman & Finnigan Reference Harman and Finnigan2021) and LES (Patton et al. Reference Patton, Sullivan and Weil2022). Analysis of these data in the streamline frame is ongoing. We believe it will provide new information on the sensitivity of the turbulent stresses to the flow distortion captured in the geometric parameters, ![]() $1/R$,
$1/R$, ![]() $1/{L_a}$,
$1/{L_a}$, ![]() $1/{L_{a2}}$,
$1/{L_{a2}}$, ![]() $1/{L_{a3}}$, and improve our empirical understanding of the relationship of these parameters and the topography. On the one hand, in the case of sparse field measurements of eddy fluxes on separate towers in the landscape, this should improve our ability to construct conservation budgets. On the other, it should lead to newer and more accurate parameterisations of complex natural flows and their practical consequences such as the estimation of landscape scale energy and carbon budgets or seed and pathogen dispersal.
$1/{L_{a3}}$, and improve our empirical understanding of the relationship of these parameters and the topography. On the one hand, in the case of sparse field measurements of eddy fluxes on separate towers in the landscape, this should improve our ability to construct conservation budgets. On the other, it should lead to newer and more accurate parameterisations of complex natural flows and their practical consequences such as the estimation of landscape scale energy and carbon budgets or seed and pathogen dispersal.
Funding
J.J.F. gratefuly acknowledges the support of The New Zealand Forest Research Institute Limited (SCION) under grant (C04×2102) during the latter stages of this work.
Declaration of interests
The author reports no conflict of interest.
Appendix A
General expressions for gradient, divergence and curl of vectors and second-order tensors in an orthonormal moving frame ![]() ${\boldsymbol{e}_i}$
${\boldsymbol{e}_i}$
 \begin{gather}
\boldsymbol{\nabla } \wedge \boldsymbol{a} =
{\boldsymbol{e}_1}[{\partial _2}{a^3} - {\partial _3}{a^2}
+ (\varGamma _{i2}^3 - \varGamma _{i3}^2){a^i}] +
{\boldsymbol{e}_2}[{\partial _3}{a^1} - {\partial _1}{a^3}
+ (\varGamma _{i3}^1 - \varGamma _{i1}^3){a^i}]\nonumber\\
\quad +\, {\boldsymbol{e}_3}[{\partial _1}{a^2} - {\partial _2}{a^1}
+ (\varGamma _{i1}^2 - \varGamma _{i2}^1){a^i}],
\end{gather}
\begin{gather}
\boldsymbol{\nabla } \wedge \boldsymbol{a} =
{\boldsymbol{e}_1}[{\partial _2}{a^3} - {\partial _3}{a^2}
+ (\varGamma _{i2}^3 - \varGamma _{i3}^2){a^i}] +
{\boldsymbol{e}_2}[{\partial _3}{a^1} - {\partial _1}{a^3}
+ (\varGamma _{i3}^1 - \varGamma _{i1}^3){a^i}]\nonumber\\
\quad +\, {\boldsymbol{e}_3}[{\partial _1}{a^2} - {\partial _2}{a^1}
+ (\varGamma _{i1}^2 - \varGamma _{i2}^1){a^i}],
\end{gather} \begin{gather}
\boldsymbol{\nabla }\boldsymbol{a} =
{\boldsymbol{e}_1}[{\partial _1}({a^i}{e_i})] +
{\boldsymbol{e}_2}[{\partial _2}({a^i}{\boldsymbol{e}_i})]
+ {\boldsymbol{e}_2}[{\partial
_2}({a^i}{\boldsymbol{e}_i})]\nonumber\\
\quad = {\boldsymbol{e}_1}[{a^i}{\partial _1}{\boldsymbol{e}_i} +
{\boldsymbol{e}_i}{\partial _1}{a^i}] +
{\boldsymbol{e}_2}[{a^i}{\partial _2}{\boldsymbol{e}_i} +
{\boldsymbol{e}_i}{\partial _2}{a^i}] +
{\boldsymbol{e}_3}[{a^i}{\partial _3}{\boldsymbol{e}_i} +
{\boldsymbol{e}_i}{\partial _3}{a^i}],
\end{gather}
\begin{gather}
\boldsymbol{\nabla }\boldsymbol{a} =
{\boldsymbol{e}_1}[{\partial _1}({a^i}{e_i})] +
{\boldsymbol{e}_2}[{\partial _2}({a^i}{\boldsymbol{e}_i})]
+ {\boldsymbol{e}_2}[{\partial
_2}({a^i}{\boldsymbol{e}_i})]\nonumber\\
\quad = {\boldsymbol{e}_1}[{a^i}{\partial _1}{\boldsymbol{e}_i} +
{\boldsymbol{e}_i}{\partial _1}{a^i}] +
{\boldsymbol{e}_2}[{a^i}{\partial _2}{\boldsymbol{e}_i} +
{\boldsymbol{e}_i}{\partial _2}{a^i}] +
{\boldsymbol{e}_3}[{a^i}{\partial _3}{\boldsymbol{e}_i} +
{\boldsymbol{e}_i}{\partial _3}{a^i}],
\end{gather}where we note that the gradient of a vector is a second-order tensor
Expression (A4) is the contraction of (A3)
In the transformed flow equations we encounter expressions involving successive directional differentiation. Because directional differentiation in the ![]() ${x^i},\;{\boldsymbol{e}_i}$ system does not commute, the order of directional differentiation must be respected. For example
${x^i},\;{\boldsymbol{e}_i}$ system does not commute, the order of directional differentiation must be respected. For example
where ![]() $\boldsymbol{a} = {a^i}{\boldsymbol{e}_i}$ is an arbitrary vector and we see from (5.14) that, in general,
$\boldsymbol{a} = {a^i}{\boldsymbol{e}_i}$ is an arbitrary vector and we see from (5.14) that, in general, ![]() $(\varGamma _{ki}^j - \varGamma _{kj}^i) \ne 0$.
$(\varGamma _{ki}^j - \varGamma _{kj}^i) \ne 0$.
Appendix B
The structure equations determine the mutual orientation of the base vectors of a moving frame. For the ![]() ${\boldsymbol{e}_i}$ Serret–Frenet basis in a general 3-D flow they can be derived most succinctly by involving the dual basis of one-forms that complements the vector basis
${\boldsymbol{e}_i}$ Serret–Frenet basis in a general 3-D flow they can be derived most succinctly by involving the dual basis of one-forms that complements the vector basis ![]() ${\boldsymbol{e}_i}$.
${\boldsymbol{e}_i}$.
Let d denote the exterior derivative (Schutz Reference Schutz1980), then
where the vector valued one-form ![]() $\boldsymbol{d}{\boldsymbol{e}_j}$, which is the exterior derivative of the base vector, is expanded in the basis with one-form coefficients,
$\boldsymbol{d}{\boldsymbol{e}_j}$, which is the exterior derivative of the base vector, is expanded in the basis with one-form coefficients, ![]() $\omega _j^i$ (Misner et al. Reference Misner, Thorne and Wheeler1970). Evidently
$\omega _j^i$ (Misner et al. Reference Misner, Thorne and Wheeler1970). Evidently
By Poincare's lemma
where ![]() ${\wedge} $ denotes exterior multiplication.
${\wedge} $ denotes exterior multiplication.
Then, since the ![]() ${\boldsymbol{e}_i}$ are linearly independent
${\boldsymbol{e}_i}$ are linearly independent
Equations (B4) are the structure equations (Finnigan Reference Finnigan1990). By combining (B3) and (B4) we obtain nine independent equations for the connection coefficients. Finnigan (Reference Finnigan1990) discusses the properties of these equations in some detail and shows that they are not integrable analytically in the general case of non-complex-lamellar flow.
Appendix C
The ![]() $\hat{\varGamma }_{jk}^i$ values for the
$\hat{\varGamma }_{jk}^i$ values for the ![]() ${x^i} = \{ \phi ,g,f\}$ metric, are as follows:
${x^i} = \{ \phi ,g,f\}$ metric, are as follows:
 \begin{equation}\left.
{\begin{array}{@{}l@{}} \varGamma_{11}^1 = \varsigma
Q\dfrac{\partial }{{\partial {x^1}}}\left(
{\dfrac{1}{{\varsigma Q}}} \right),\quad \varGamma_{22}^2 =
\dfrac{Q}{2}\dfrac{\partial }{{\partial {x^2}}}\left(
{\dfrac{1}{Q}} \right),\\
\varGamma_{33}^3 = \dfrac{Q}{2}\dfrac{\partial }{{\partial {x^3}}}\left(
{\dfrac{1}{Q}} \right),\quad \varGamma_{12}^1 = \varGamma_{21}^1
= \varsigma Q\dfrac{\partial }{{\partial {x^2}}}\left(
{\dfrac{1}{{\varsigma Q}}} \right),\\
\varGamma_{22}^1 =
\dfrac{{{\varsigma^2}}}{2}\dfrac{{\partial Q}}{{\partial
{x^1}}},\quad \varGamma_{12}^2 = \varGamma_{21}^2 =
Q\dfrac{\partial }{{\partial {x^1}}}\left( {\dfrac{1}{Q}} \right),\\
\varGamma_{11}^2 ={-} \dfrac{Q}{2}\dfrac{\partial }{{\partial {x^2}}}\left(
{\dfrac{1}{{{\varsigma^2}{Q^2}}}} \right),\quad
\varGamma_{13}^2 = \varGamma_{31}^2 = \varGamma_{12}^3 =
\varGamma_{21}^3 = 0,\\
\varGamma_{33}^1 =
\dfrac{{{\varsigma^2}}}{2}\dfrac{{\partial Q}}{{\partial
{x^1}}},\quad \varGamma_{31}^1 = \varGamma_{13}^1 = \varsigma
Q\dfrac{\partial }{{\partial {x^3}}}\left(
{\dfrac{1}{{\varsigma Q}}} \right),\\
\varGamma_{33}^2 ={-} \dfrac{Q}{2}\dfrac{\partial }{{\partial {x^2}}}\left(
{\dfrac{1}{Q}} \right),\quad \varGamma_{11}^3 ={-}
\dfrac{Q}{2}\dfrac{\partial }{{\partial {x^3}}}\left(
{\dfrac{1}{{{\varsigma^2}{Q^2}}}} \right),\\
\varGamma_{22}^3 ={-} \dfrac{Q}{2}\dfrac{\partial }{{\partial
{x^3}}}\left( {\dfrac{1}{Q}} \right),\quad \varGamma_{23}^2 =
\varGamma_{32}^2 = \dfrac{Q}{2}\dfrac{\partial }{{\partial
{x^3}}}\left( {\dfrac{1}{Q}} \right),\\
\varGamma_{13}^3 = \varGamma_{31}^3 = \dfrac{Q}{2}\dfrac{\partial }{{\partial
{x^1}}}\left( {\dfrac{1}{Q}} \right),\quad \varGamma_{23}^3 =
\varGamma_{32}^3 = \dfrac{Q}{2}\dfrac{\partial }{{\partial
{x^2}}}\left( {\dfrac{1}{Q}} \right). \end{array}}
\right\}\end{equation}
\begin{equation}\left.
{\begin{array}{@{}l@{}} \varGamma_{11}^1 = \varsigma
Q\dfrac{\partial }{{\partial {x^1}}}\left(
{\dfrac{1}{{\varsigma Q}}} \right),\quad \varGamma_{22}^2 =
\dfrac{Q}{2}\dfrac{\partial }{{\partial {x^2}}}\left(
{\dfrac{1}{Q}} \right),\\
\varGamma_{33}^3 = \dfrac{Q}{2}\dfrac{\partial }{{\partial {x^3}}}\left(
{\dfrac{1}{Q}} \right),\quad \varGamma_{12}^1 = \varGamma_{21}^1
= \varsigma Q\dfrac{\partial }{{\partial {x^2}}}\left(
{\dfrac{1}{{\varsigma Q}}} \right),\\
\varGamma_{22}^1 =
\dfrac{{{\varsigma^2}}}{2}\dfrac{{\partial Q}}{{\partial
{x^1}}},\quad \varGamma_{12}^2 = \varGamma_{21}^2 =
Q\dfrac{\partial }{{\partial {x^1}}}\left( {\dfrac{1}{Q}} \right),\\
\varGamma_{11}^2 ={-} \dfrac{Q}{2}\dfrac{\partial }{{\partial {x^2}}}\left(
{\dfrac{1}{{{\varsigma^2}{Q^2}}}} \right),\quad
\varGamma_{13}^2 = \varGamma_{31}^2 = \varGamma_{12}^3 =
\varGamma_{21}^3 = 0,\\
\varGamma_{33}^1 =
\dfrac{{{\varsigma^2}}}{2}\dfrac{{\partial Q}}{{\partial
{x^1}}},\quad \varGamma_{31}^1 = \varGamma_{13}^1 = \varsigma
Q\dfrac{\partial }{{\partial {x^3}}}\left(
{\dfrac{1}{{\varsigma Q}}} \right),\\
\varGamma_{33}^2 ={-} \dfrac{Q}{2}\dfrac{\partial }{{\partial {x^2}}}\left(
{\dfrac{1}{Q}} \right),\quad \varGamma_{11}^3 ={-}
\dfrac{Q}{2}\dfrac{\partial }{{\partial {x^3}}}\left(
{\dfrac{1}{{{\varsigma^2}{Q^2}}}} \right),\\
\varGamma_{22}^3 ={-} \dfrac{Q}{2}\dfrac{\partial }{{\partial
{x^3}}}\left( {\dfrac{1}{Q}} \right),\quad \varGamma_{23}^2 =
\varGamma_{32}^2 = \dfrac{Q}{2}\dfrac{\partial }{{\partial
{x^3}}}\left( {\dfrac{1}{Q}} \right),\\
\varGamma_{13}^3 = \varGamma_{31}^3 = \dfrac{Q}{2}\dfrac{\partial }{{\partial
{x^1}}}\left( {\dfrac{1}{Q}} \right),\quad \varGamma_{23}^3 =
\varGamma_{32}^3 = \dfrac{Q}{2}\dfrac{\partial }{{\partial
{x^2}}}\left( {\dfrac{1}{Q}} \right). \end{array}}
\right\}\end{equation}