Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T15:43:20.436Z Has data issue: false hasContentIssue false
  • English
  • Français

Stretching and mixing in sheared particulate suspensions

Published online by Cambridge University Press:  05 January 2017

M. Souzy ,
H. Lhuissier ,
E. Villermaux  and
B. Metzger
M. Souzy
Affiliation:
Aix Marseille Université, CNRS, IUSTI UMR 7343, 13453 Marseille, France
H. Lhuissier
Affiliation:
Aix Marseille Université, CNRS, IUSTI UMR 7343, 13453 Marseille, France
E. Villermaux
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE UMR 7342, 13384 Marseille, France Institut Universitaire de France, Paris, France
B. Metzger*
Affiliation:
Aix Marseille Université, CNRS, IUSTI UMR 7343, 13453 Marseille, France
*
†Email address for correspondence: bloen.metzger@univ-amu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We experimentally investigate mixing in sheared particulate suspensions by measuring a crucial kinematic quantity of the flow: the stretching laws of material lines in the suspending liquid. High-resolution particle image velocimetry (PIV) measurements in the fluid phase are performed to reconstruct, following the Diffusive Strip Method (Meunier & Villermaux, J. Fluid Mech., vol. 662, 2010, pp. 134–172), the stretching histories of the fluid material lines. In a broad range of volume fractions 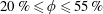$20\,\%\leqslant \unicode[STIX]{x1D719}\leqslant 55\,\%$ , the nature of the elongation law changes drastically from linear, in the absence of particles, to exponential in the presence of particles: the mean and the standard deviation of the material line elongations are found to grow exponentially in time and the distribution of elongations converges to a log-normal. A multiplicative stretching model, based on the distribution of local shear rates and on their persistence time, is derived. This model quantitatively captures the experimental stretching laws. The presence of particles is shown to accelerate mixing at large Péclet numbers ( 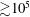${\gtrsim}10^{5}$ ). However, the wide distribution of stretching rates results in heterogeneous mixing and, hence, broadly distributed mixing times, in qualitative agreement with experimental observations.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Flow Control: Mixing enhancement Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 611 - 635
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afonso, M. M. & Vincenzi, D. 2005 Nonlinear elastic polymers in random flow. J. Fluid Mech. 540, 99–108.Google Scholar
Arp, P. A. & Mason, S. G. 1976 The kinetics of flowing dispersions IX. Doublets of rigid spheres (experimental). J. Colloid Interface Sci. 61 (4095), 44–61.Google Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in a turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.Google Scholar
Boyer, F., Guazzelli, E. & Pouliquen, O. 2011 Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.Google Scholar
Breedveld, V., van den Ende, D., Bosscher, M., Jongschaap, R. J. J. & Mellema, J. 2002 Measurement of the full shear-induced self-diffusion tensor of noncolloidal suspensions. J. Chem. Phys. 116, 23, 10529–10535.Google Scholar
Buch, K. A. Jr & Dahm, W. J. A. 1996 Experimental study of the fine-scale structure of conserved scalar mixing in turbulent shear flows. J. Fluid Mech. 317 (Part 1), 21–71.Google Scholar
Chateau, X., Ovarlez, G. & Trung, K. L. 2008 Homogenization approach to the behavior of suspensions of noncolloidal particles in yield stress fluids. J. Rheol. 52, 489–506.Google Scholar
Cocke, W. J. 1969 Turbulent hydrodynamic line stretching: consequences of isotropy. Phys. Fluids 12 (12), 2488–2492.Google Scholar
Cocke, W. J. 1971 Turbulent hydrodynamic line-stretching: the random walk limit. Phys. Fluids 14 (8), 1624–1628.Google Scholar
Culbertson, C. T., Jacobson, S. C. & Ramsey, J. M. 2002 Diffusion coefficient measurements in microfluidic devices. Talanta 56, 365–373.Google Scholar
Da Cunha, F. R. & Hinch, E. J. 1996 Shear-induced dispersion in a dilute suspension of rough spheres. J. Fluid Mech. 309, 211–223.CrossRefGoogle Scholar
Dagois-Bohy, S., Hormozi, S., Guazzelli, E. & Pouliquen, O. 2015 Rheology of dense suspensions of non-colloidal spheres in yield-stress fluids. J. Fluid Mech. 776, R2.CrossRefGoogle Scholar
Dasan, J., Ramamohan, T. R., Singh, A. & Nott, P. 2002 Stress fluctuations in sheared Stokesian suspensions. Phys. Rev. E 66, 021409.Google Scholar
Drazer, G., Koplik, J., Khusid, B. & Acrivos, A. 2002 Deterministic and stochastic behaviour of non-Brownian spheres in sheared suspensions. J. Fluid Mech. 460, 307–335.Google Scholar
Duplat, J., Innocenti, C. & Villermaux, E. 2010 A nonsequential turbulent mixing process. Phys. Fluids 22, 035104.Google Scholar
Duplat, J. & Villermaux, E. 2000 Persistence of material element deformation in isotropic flows and growth rate of lines and surfaces. Eur. Phys. J. B 18, 353–361.Google Scholar
Duplat, J. & Villermaux, E. 2008 Mixing by random stirring in confined mixtures. J. Fluid Mech. 617, 51–86.Google Scholar
Eckstein, E. C., Bailey, D. G. & Shapiro, A. H. 1977 Self-diffusion of particles in shear flow of a suspension. J. Fluid Mech. 79, 191–208.Google Scholar
Girimaji, S. S. & Pope, S. B. 1990 Material-element deformation in isotropic turbulence. J. Fluid Mech. 220, 427–458.CrossRefGoogle Scholar
Harlen, O. G. & Koch, D. L. 1993 Simple shear flow of a suspension of fibres in a dilute polymer solution at high Deborah number. J. Fluid Mech. 252, 187–207.Google Scholar
Le Borgne, T., Dentz, M. & Villermaux, E. 2015 The lamellar description of mixing in porous media. J. Fluid Mech. 770, 458–498.Google Scholar
Lerner, E., Dring, G. & Wyart, M. 2015 A unified framework for non-Brownian suspension flows and soft amorphous solids. Proc. Natl Acad. Sci. USA 109, 4798–4803.Google Scholar
Metzger, B. & Butler, J. E. 2012a Clouds of particles in a periodic shear flow. Phys. Fluids 24, 021703.Google Scholar
Metzger, B. & Butler, J. E. 2012b Irreversibility and chaos: role of long-range hydrodynamic interactions in sheared suspensions. Phys. Rev. E 82, 051406.Google Scholar
Metzger, B., Pham, P. & Butler, J. E. 2013 Irreversibility and chaos: role of lubrication interactions in sheared suspensions. Phys. Rev. E 87, 052304.Google Scholar
Metzger, B., Rahli, O. & Yin, X. 2013 Heat transfer across sheared suspensions: role of the shear-induced diffusion. J. Fluid Mech. 724, 527–552.Google Scholar
Meunier, P. & Leweke, T. 2003 Analysis and minimization of errors due to high gradients in particle image velocimetry. Exp. Fluids 35, 408–421.Google Scholar
Meunier, P. & Villermaux, E. 2003 How vortices mix. J. Fluid Mech. 476, 213–222.Google Scholar
Meunier, P. & Villermaux, E. 2010 The diffusive strip method for scalar mixing in two dimensions. J. Fluid Mech. 662, 134–172.Google Scholar
Orszag, S. A. 1970 Comments on ‘Turbulent hydrodynamic line stretching: consequences of isotropy’. Phys. Fluids 13, 2203–2204.Google Scholar
Ottino, J. M. 1989 The Kinematics of Mixing: Stretching, Chaos, and Transport. Cambridge University Press.Google Scholar
Ranz, W. E. 1979 Applications of a stretch model diffusion, and reaction in laminar and turbulent flows. AIChE J. 25, 1.CrossRefGoogle Scholar
Shaqfeh, E. S. G. & Koch, D. L. 1992 Polymer stretch in dilute fixed beds of fibres or spheres. J. FLuid Mech. 244, 17–54.Google Scholar
Sierou, A. & Brady, J. F. 2004 Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid Mech. 506, 285–314.Google Scholar
Sohn, C. W. & Chen, M. M. 1984 Heat Transfer enhancement in laminar slurry pipe flows with power law thermal conductivities. Trans. ASME J. Heat Transfer 106, 539–542.Google Scholar
Souzy, M., Yin, X., Villermaux, E., Abid, C. & Metzger, B. 2015 Super-diffusion in sheared suspensions. Phys. Fluids 27, 041705.Google Scholar
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 1137.Google Scholar
Trulsson, M., DeGiuli, E. & Wyart, M.2016 Effect of friction on dense suspension flows of hard particles. Preprint, 2016 (https://arxiv.org/abs/1606.07650).Google Scholar
Villermaux, E. 2012 On dissipation in stirred mixtures. Adv. Appl. Mech. 45, 91–107.Google Scholar
Wang, N. L. & Keller, K. H. 1985 Augmented transport of extracellular solutes in concentrated erythrocyte suspensions in couette flow. J. Colloid Interface Sci. 103, 210–225.Google Scholar
Wang, L., Koch, D. L., Yin, X. & Cohen, C. 2009 Hydrodynamic diffusion and mass transfer across a sheared suspension of neutrally buoyant spheres. Phys. Fluids 21, 033303.Google Scholar

Souzy et al. supplementary movie

Slice of a sheared suspension of volume fraction \phi=0.35 illuminated by a laser sheet. The small fluorescent tracers seeding the suspending fluid appear as bright whereas the particle intersections with the laser sheet appear as dark. The particle diametre d=2 mm.

Download Souzy et al. supplementary movie(Video)
Video 14 MB

Souzy et al. supplementary movie

Comparison of the stretching process of a blob of dye (in black) sheared at high Péclet (Pe=10^6) and low Reynolds number (Re=10^{-4}) in a pure fluid (top), and in a particulate suspension with volume fraction \phi=35\%.

Download Souzy et al. supplementary movie(Video)
Video 7.3 MB

Souzy et al. supplementary movie

Example of stretching for two material lines numerically advected using the experimental fluid velocity field. One line successively stretches and folds very similarly to what is observed in the blob experiments (Movie 2). Interestingly, the other line behaves very differently. Although it sustains the same macroscopic strain, it experiences a much softer stretching only because it started from a different initial location. These different stretching histories reveal the stochastic nature of the stretching induced within particulate suspensions.

Download Souzy et al. supplementary movie(Video)
Video 12.4 MB