Hostname: page-component-76c49bb84f-t7r7g Total loading time: 0 Render date: 2025-07-07T19:19:16.392Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly nonlinear effects on internal solitary waves in three-layer flows

Published online by Cambridge University Press:  25 November 2019

Ricardo Barros Open the ORCID record for Ricardo Barros [Opens in a new window] ,
Wooyoung Choi Open the ORCID record for Wooyoung Choi [Opens in a new window]  and
Paul A. Milewski Open the ORCID record for Paul A. Milewski [Opens in a new window]
Ricardo Barros*
Affiliation:
Department of Mathematical Sciences, Loughborough University, LoughboroughLE11 3TU, UK
Wooyoung Choi
Affiliation:
Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, NJ07102-1982, USA
Paul A. Milewski
Affiliation:
Department of Mathematical Sciences, University of Bath, Claverton Down, BathBA2 7AY, UK
*
†Email address for correspondence: r.barros@lboro.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

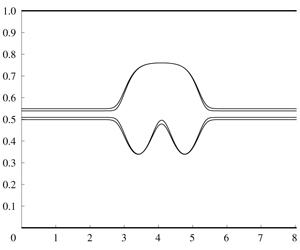
We consider a strongly nonlinear long wave model for large amplitude internal waves in a three-layer flow between two rigid boundaries. The model extends the two-layer Miyata–Choi–Camassa (MCC) model (Miyata, Proceedings of the IUTAM Symposium on Nonlinear Water Waves, eds. H. Horikawa & H. Maruo, 1988, pp. 399–406; Choi & Camassa, J. Fluid Mech., vol. 396, 1999, pp. 1–36) and is able to describe the propagation of long internal waves of both the first and second baroclinic modes. Solitary-wave solutions of the model are shown to be governed by a Hamiltonian system with two degrees of freedom. Emphasis is given to the solitary waves of the second baroclinic mode (mode 2) and their strongly nonlinear characteristics that fail to be captured by weakly nonlinear models. In certain asymptotic limits relevant to oceanic applications and previous laboratory experiments, it is shown that large amplitude mode-2 waves with single-hump profiles can be described by the solitary-wave solutions of the MCC model, originally developed for mode-1 waves in a two-layer system. In other cases, however, e.g. when the density stratification is weak and the density transition layer is thin, the richness of the dynamical system with two degrees of freedom becomes apparent and new classes of mode-2 solitary-wave solutions of large amplitudes, characterized by multi-humped wave profiles, can be found. In contrast with the classical solitary-wave solutions described by the MCC equation, such multi-humped solutions cannot exist for a continuum set of wave speeds for a given layer configuration. Our analytical predictions based on asymptotic theory are then corroborated by a numerical study of the original Hamiltonian system.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows Waves/Free-surface Flows: Solitary waves

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A16
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions (ed. Abramowitz, M. & Stegun, I. A.), Applied mathematics series, vol. 55, p. 39. National Bureau of Standards.Google Scholar
Akylas, T. R. & Grimshaw, R. H. J. 1992 Solitary internal waves with oscillatory tails. J. Fluid Mech. 242, 279–298.CrossRefGoogle Scholar
Barros, R. 2016 Remarks on a strongly nonlinear model for two-layer flows with a top free surface. Stud. Appl. Maths 136, 263–287.CrossRefGoogle Scholar
Barros, R. & Gavrilyuk, S. L. 2007 Dispersive nonlinear waves in two-layer flows with free surface. II. Large amplitude solitary waves embedded into the continuous spectrum. Stud. Appl. Maths 119, 213–251.CrossRefGoogle Scholar
Benjamin, T. B. 1966 Internal waves of finite amplitude and permanent form. J. Fluid Mech. 25, 241–270.CrossRefGoogle Scholar
Benney, D. J. 1966 Long non-linear waves in fluid flow. J. Math. Phys. 45, 52–63.CrossRefGoogle Scholar
Camassa, R., Choi, W., Michallet, H., Rusas, P. & Sveen, J. K. 2006 On the realm of validity of strongly nonlinear asymptotic approximations for internal waves. J. Fluid Mech. 549, 1–23.CrossRefGoogle Scholar
Carr, M., Davies, P. A. & Hoebers, R. P. 2015 Experiments on the structure and stability of mode-2 internal solitary-like waves propagating on an offset pycnocline. Phys. Fluids 27, 046602.CrossRefGoogle Scholar
Choi, W. 2000 Modeling of strongly nonlinear internal waves in a multilayer system. In Proceedings of the Fourth International Conference on Hydrodynamics (ed. Goda, Y., Ikehata, M. & Suzuki, K.), pp. 453–458. ICHD2000 Local Organizing Committee.Google Scholar
Choi, W. & Camassa, R. 1999 Fully nonlinear internal waves in a two-fluid system. J. Fluid Mech. 396, 1–36.CrossRefGoogle Scholar
Davis, R. E. & Acrivos, A. 1967 Solitary internal waves in deep water. J. Fluid Mech. 29 (3), 593–607.CrossRefGoogle Scholar
Gavrilov, N. V. & Liapidevskii, V. Y. 2010 Finite-amplitude solitary waves in a two-layer fluid. J. Appl. Mech. Tech. Phys. 51, 471–481.CrossRefGoogle Scholar
Gavrilov, N. V., Liapidevskii, V. Yu. & Gavrilova, K. 2011 Large amplitude internal solitary waves over a shelf. Nat. Hazards Earth Syst. Sci. 11, 17–25.CrossRefGoogle Scholar
Gavrilov, N. V., Liapidevskii, V. Yu. & Liapidevskaya, Z. A. 2013 Influence of dispersion on the propagation of the internal waves in the shelf zone. Fundam. Appl. Hydrophy. 6, 25–34 (in Russian).Google Scholar
Grimshaw, R. 1981 Evolution equations for long nonlinear waves in stratified shear flow. Stud. Appl. Maths 65, 159–188.CrossRefGoogle Scholar
Helfrich, K. R. & Melville, W. K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38, 395–425.CrossRefGoogle Scholar
Jo, T.-C. & Choi, Y.-K. 2014 Dynamics of strongly nonlinear internal long waves in a three-layer fluid system. Ocean Sci. J. 49 (4), 357–366.CrossRefGoogle Scholar
Kurkina, O. E., Kurkin, A. A., Rouvinskaya, E. A. & Soomere, T. 2015 Propagation regimes of interfacial solitary waves in a three-layer fluid. Nonlinear Process. Geophys. 22, 117–132.CrossRefGoogle Scholar
Lamb, K. G. 2000 Conjugate flows for a three-layer fluid. Phys. Fluids 12, 2169–2185.CrossRefGoogle Scholar
Liu, L., Moore, G. & Russell, R. D. 1997 Computation and continuation of homoclinic and heteroclinic orbits with arclength parameterization. SIAM J. Sci. Comput. 18 (1), 69–93.CrossRefGoogle Scholar
Liu, P. L.-F. & Wang, X. 2012 A multi-layer model for nonlinear internal wave propagation in shallow water. J. Fluid Mech. 695, 341–365.CrossRefGoogle Scholar
Maxworthy, T. 1980 On the formation of nonlinear internal waves from the gravitational collapse of mixed regions in two and three dimensions. J. Fluid Mech. 96, 47–64.CrossRefGoogle Scholar
Miyata, M. 1988 Long internal waves of large amplitude. In Proceedings of the IUTAM Symposium on Nonlinear Water Waves (ed. Horikawa, H. & Maruo, H.), pp. 399–406. Springer.CrossRefGoogle Scholar
Olsthoorn, J., Baglaenko, A. & Stastna, M. 2013 Analysis of asymmetries in propagating mode-2 waves. Nonlinear Process. Geophys. 20 (1), 59–69.CrossRefGoogle Scholar
Prasolov, V. V. 2004 Polynomials, Algorithms and Computation in Mathematics. Springer.Google Scholar
Rosenau, P. R. 2005 What is …a compacton? Not. Amer. Math. Soc. 52 (7), 738–739.Google Scholar
Rusas, P.-O. & Grue, J. 2002 Solitary waves and conjugate flows in a three-layer fluid. Eur. J. Mech. (B/Fluids) 21, 185–206.CrossRefGoogle Scholar
Shroyer, E. L., Moum, J. N. & Nash, J. D. 2010 Mode 2 waves on the continental shelf: Ephemeral components of the nonlinear internal wavefield. J. Geophys. Res. 115, C07001.CrossRefGoogle Scholar
Terez, D. E. & Knio, O. M. 1998 Numerical simulations of large-amplitude internal solitary waves. J. Fluid Mech. 362, 53–82.CrossRefGoogle Scholar
Terletska, K., Jung, K. T., Talipova, T., Maderich, V., Brovchenko, I. & Grimshaw, R. 2016 Internal breather-like wave generation by the second mode solitary wave interaction with a step. Phys. Fluids 28 (11), 116602.CrossRefGoogle Scholar
Tung, K.-K., Chan, T. F. & Kubota, T. 1982 Large amplitude internal waves of permanent form. Stud. Appl. Maths 66, 1–44.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. & Turner, R. E. L. 1992 Long periodic internal waves. Phys. Fluids A 4 (9), 1929–1935.CrossRefGoogle Scholar
Yang, J. 2010 Nonlinear Waves in Integrable and Nonintegrable Systems, vol. 16. SIAM.CrossRefGoogle Scholar
Yang, J., Malomed, B. A. & Kaup, D. J. 1991 Embedded solitons in second-harmonic-generating systems. Phys. Rev. Lett. 83, 1958–1961.CrossRefGoogle Scholar
Yang, Y. J., Fang, Y. C., Tang, T. Y. & Ramp, S. R. 2010 Convex and concave types of second baroclinic mode internal solitary waves. Nonlinear Proc. Geophys. 17, 605–614.CrossRefGoogle Scholar
Yuan, C., Grimshaw, R. & Johnson, E. 2018 The evolution of second mode internal solitary waves over variable topography. J. Fluid Mech. 836, 238–259.CrossRefGoogle Scholar