Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T07:29:19.714Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure and stability of Joukowski's rotor wake model

Published online by Cambridge University Press:  25 January 2021

E. Durán Venegas Open the ORCID record for E. Durán Venegas [Opens in a new window] ,
P. Rieu  and
S. Le Dizès Open the ORCID record for S. Le Dizès [Opens in a new window]
E. Durán Venegas
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE, 13384Marseille, France Departamento de Bioingeniería e Ingeniería Aeroespacial, Universidad Carlos III de Madrid, 28911Madrid, Spain
P. Rieu
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE, 13384Marseille, France
S. Le Dizès*
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE, 13384Marseille, France
*
†Email address for correspondence: stephane.ledizes@univ-amu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

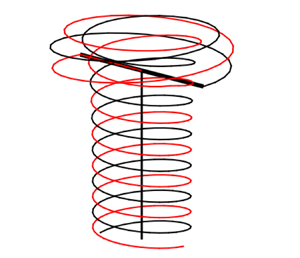
In this work, Joukowski's rotor wake model is considered for a two-blade rotor of radius $R_b$ rotating at the angular velocity $\varOmega _R$ in a normal incident velocity $V_{\infty }$. This model is based on a description of the wake by a limited number of vortices of core size $a$: a tip vortex of constant circulation $\varGamma$ for each blade and a root vortex of circulation $-2\varGamma$ on the rotation axis. Using a free-vortex method, we obtain solutions matching uniform interlaced helices in the far field that are steady in the frame rotating with the rotor for a large range of tip-speed ratios $\lambda = R_b \Omega _R/V_{\infty }$ and vortex strengths $\eta = \varGamma /(R_b^{2} \Omega _R)$. Solutions are provided for a two-bladed rotor for both helicopters and wind turbines. Particular attention is brought to the study of the solutions describing steep-descent helicopter flight regimes and large tip-ratio wind turbine regimes, for which the vortex structure is strongly deformed in the near wake and crosses the rotor plane. Both the geometry of the structure and its induced velocity field are analysed in detail. The thrust and the power coefficient of the solutions are also provided and compared to the momentum theory. The stability of the solutions is studied by monitoring the linear spatio-temporal development of a localized perturbation placed at different locations. Good agreements with the theoretical predictions for uniform helices and for point vortex arrays are demonstrated for the stability properties in the far wake. However, a more complex evolution is observed for the more deformed solutions when the perturbation is placed close to the rotor.

JFM classification

Aerodynamics: Aerodynamics Wakes/Jets: Wakes/Jets Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , A6
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Betz, A. 1920 Das maximum der theoretisch möglichen ausnützung des windes durch windmotoren. Zeitschrift das gesamte Turbinewessen.Google Scholar
Blanco-Rodríguez, F.J. & Le Dizès, S. 2016 Elliptic instability of a curved Batchelor vortex. J. Fluid Mech. 804, 224–247.CrossRefGoogle Scholar
Blanco-Rodríguez, F.J. & Le Dizès, S. 2017 Curvature instability of a curved Batchelor vortex. J. Fluid Mech. 814, 397–415.CrossRefGoogle Scholar
Bolnot, H., Le Dizès, S. & Leweke, T. 2014 Spatio-temporal development of the pairing instability in an infinite array of vortex rings. Fluid Dyn. Res. 46, 061405.CrossRefGoogle Scholar
Branlard, E. & Gaunaa, M. 2015 Cylindrical vortex wake model: right cylinder. Wind Energ. 18, 1973–1987.CrossRefGoogle Scholar
Brynjell-Rahkola, M. & Henningson, D.S. 2020 Numerical realization of helical vortices: application to vortex instability. Theor. Comput. Fluid Dyn. 34, 1–20.CrossRefGoogle Scholar
Chattot, J.-J. 2003 Optimization of wind turbines using helicoidal vortex model. J. Sol. Energy Engng 125, 418–424.CrossRefGoogle Scholar
Da Rios, L.S. 1916 Vortici ad elica. Il Nuovo Cimento 11, 419–431.CrossRefGoogle Scholar
Drees, J.M. & Hendal, W.P. 1951 The field of flow through a helicopter rotor obtained from wind tunnel smoke tests. J. Aircraft Engng 23, 107–111.Google Scholar
Durán Venegas, E. & Le Dizès, S. 2019 Generalized helical vortex pairs. J. Fluid Mech. 865, 523–545.CrossRefGoogle Scholar
Durán Venegas, E., Le Dizès, S. & Eloy, C. 2019 A strongly-coupled model for flexible rotors. J. Fluids Struct. 89, 219–231.CrossRefGoogle Scholar
Fukumoto, Y. & Miyazaki, T. 1991 Three-dimensional distorsions of a vortex filament with axial velocity. J. Fluid Mech. 222, 369–416.CrossRefGoogle Scholar
Goldstein, M.A. 1929 On the vortex theory of screw propellers. Proc. R. Soc. Lond. A 123, 440–465.Google Scholar
Green, R.B., Gillies, E.A. & Brown, R.E. 2005 The flow field around a rotor in axial descent. J. Fluid Mech. 534, 237–261.CrossRefGoogle Scholar
Gupta, B.P. & Loewy, R.G. 1974 Theoretical analysis of the aerodynamic stability of multiple, interdigitated helical vortices. AIAA J. 12, 1381–1387.CrossRefGoogle Scholar
Hansen, M.O.L. 2015 Aerodynamics of Wind Turbines, 3rd edn. Routledge.CrossRefGoogle Scholar
Hardin, J.C. 1982 The velocity field induced by a helical vortex filament. Phys. Fluids 25, 1949–1952.CrossRefGoogle Scholar
Hattori, Y., Blanco-Rodríguez, F.J. & Le Dizès, S. 2019 Numerical stability analysis of a vortex ring with swirl. J. Fluid Mech. 878, 5–36.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P.A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Ivanell, S., Mikkelsen, R., Sørensen, J.N. & Henningson, D. 2010 Stability analysis of the tip vortices of a wind turbine. Wind Energy 13, 705–715.CrossRefGoogle Scholar
Joukowski, N. 1929 Théorie tourbillonnaire de l'hélice propulsive. Gauthier-Villars.Google Scholar
Kelvin, Lord 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Leishman, J.G. 2006 Principles of Helicopter Aerodynamics. Cambridge University Press.Google Scholar
Leishman, J.G., Bhagwat, M.J. & Bagai, A. 2002 Free-vortex filament methods for the analysis of helicopter rotor wakes. J. Aircraft 39, 759–775.CrossRefGoogle Scholar
Leweke, T., Quaranta, H.U., Bolnot, H., Blanco-Rodríguez, F.J. & Le Dizès, S. 2014 Long- and short-wave instabilities in helical vortices. J. Phys.: Conf. Ser. 524, 012154.Google Scholar
Okulov, V.L. 2004 On the stability of multiple helical vortices. J. Fluid Mech. 521, 319–342.CrossRefGoogle Scholar
Okulov, V.L. & Sørensen, J.N. 2007 Stability of helical tip vortices in a rotor far wake. J. Fluid Mech. 576, 1–25.CrossRefGoogle Scholar
Okulov, V.L. & Sørensen, J.N. 2010 Maximum efficiency of wind turbine rotors using Joukowsky and Betz approaches. J. Fluid Mech. 649, 497–508.CrossRefGoogle Scholar
Okulov, V.L. & Sørensen, J.N. 2020 The self-induced motion of a helical vortex. J. Fluid Mech. 883, A5.CrossRefGoogle Scholar
Quaranta, U. 2017 Instabilities in a swirling rotor wake. PhD thesis, Aix Marseille Université.Google Scholar
Quaranta, H.U., Bolnot, H. & Leweke, T. 2015 Long-wave instability of a helical vortex. J. Fluid Mech. 780, 687–716.CrossRefGoogle Scholar
Quaranta, H.U., Brynjell-Rahkola, M., Leweke, T. & Henningson, D.S. 2018 Local and global pairing instabilities of two interlaced helical vortices. J. Fluid Mech. 863, 927–955.CrossRefGoogle Scholar
Saffman, P.G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Sarmast, R., Dadfar, R., Mikkelsen, R.F., Schlatter, P., Ivanell, S., Sørensen, J.N. & Henningson, D. 2014 Mutual inductance instability of the tip vortices behind a wind turbine. J. Fluid Mech. 755, 705–731.CrossRefGoogle Scholar
Selçuk, C., Delbende, I. & Rossi, M. 2018 Helical vortices: linear stability analysis and nonlinear dynamics. Fluid Dyn. Res. 50, 011411.CrossRefGoogle Scholar
Sørensen, J.N. & Shen, W.Z. 2002 Numerical modeling of wind turbine wakes. J. Fluids Engng 124, 393–399.CrossRefGoogle Scholar
Sørensen, J.N. 2016 General Momentum Theory for Horizontal Axis Wind Turbines. Springer Series: Research Topics in Wind Energy, vol. 4. Springer.CrossRefGoogle Scholar
Stack, J., Caradonna, F.X. & Savaş, Ö. 2005 Flow visualizations and extended thrust time histories of rotor vortex wakes in descent. J. Am. Helicopter Soc. 50, 279–288.CrossRefGoogle Scholar
Velasco Fuentes, O. 2018 Motion of a helical vortex. J. Fluid Mech. 836, R1.CrossRefGoogle Scholar
Widnall, S.E. 1972 The stability of a helical vortex filament. J. Fluid Mech. 54, 641–663.CrossRefGoogle Scholar
Wood, D.H., Okulov, V.L. & Bhattacharjee, D. 2017 Direct calculation of wind turbine tip loss. Renew. Energy 95, 269–276.CrossRefGoogle Scholar