Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T08:42:30.679Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure of a highly decelerated axisymmetric turbulent boundary layer

Published online by Cambridge University Press:  19 October 2021

N. Agastya Balantrapu Open the ORCID record for N. Agastya Balantrapu [Opens in a new window] ,
Christopher Hickling ,
W. Nathan Alexander  and
William Devenport
N. Agastya Balantrapu
Affiliation:
Department of Aerospace and Ocean Engineering, Virginia Tech, Blacksburg, VA 24060, USA
Christopher Hickling
Affiliation:
Department of Aerospace and Ocean Engineering, Virginia Tech, Blacksburg, VA 24060, USA
W. Nathan Alexander
Affiliation:
Department of Aerospace and Ocean Engineering, Virginia Tech, Blacksburg, VA 24060, USA
William Devenport*
Affiliation:
Department of Aerospace and Ocean Engineering, Virginia Tech, Blacksburg, VA 24060, USA
*
†Email address for correspondence: devenport@vt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

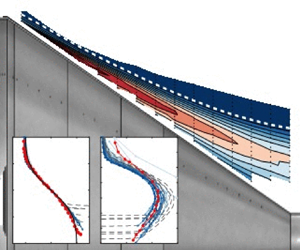
Experiments were performed over a body of revolution at a length-based Reynolds number of 1.9 million. While the lateral curvature parameters are moderate ($\delta /r_s < 2, r_s^+>500$, where $\delta$ is the boundary layer thickness and rs is the radius of curvature), the pressure gradient is increasingly adverse ($\beta _{C} \in [5 \text {--} 18]$ where $\beta_{C}$ is Clauser’s pressure gradient parameter), representative of vehicle-relevant conditions. The mean flow in the outer regions of this fully attached boundary layer displays some properties of a free-shear layer, with the mean-velocity and turbulence intensity profiles attaining self-similarity with the ‘embedded shear layer’ scaling (Schatzman & Thomas, J. Fluid Mech., vol. 815, 2017, pp. 592–642). Spectral analysis of the streamwise turbulence revealed that, as the mean flow decelerates, the large-scale motions energize across the boundary layer, growing proportionally with the boundary layer thickness. When scaled with the shear layer parameters, the distribution of the energy in the low-frequency region is approximately self-similar, emphasizing the role of the embedded shear layer in the large-scale motions. The correlation structure of the boundary layer is discussed at length to supply information towards the development of turbulence and aeroacoustic models. One major finding is that the estimation of integral turbulence length scales from single-point measurements, via Taylor's hypothesis, requires significant corrections to the convection velocity in the inner 50 % of the boundary layer. The apparent convection velocity (estimated from the ratio of integral length scale to the time scale), is approximately 40 % greater than the local mean velocity, suggesting the turbulence is convected much faster than previously thought. Closer to the wall even higher corrections are required.

JFM classification

Boundary Layers: Boundary layer structure Acoustics: Aeroacoustics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 929 , 25 December 2021 , A9
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Atkinson, C., Buchmann, N.A., Amili, O. & Soria, J. 2013 On the appropriate filtering of PIV measurements of turbulent shear flows. Exp. Fluids 55 (1), 1654.CrossRefGoogle Scholar
Atkinson, C., Buchmann, N.A. & Soria, J. 2015 An experimental investigation of turbulent convection velocities in a turbulent boundary layer. Flow Turbul. Combust. 94 (1), 79–95.CrossRefGoogle Scholar
Bearman, P.W. 1971 Corrections for the effect of ambient temperature drift on hot-wire measurements in incompressible flow. DISA Inform. 11, 25–30.Google Scholar
Bobke, A., Vinuesa, R., Örlü, R. & Schlatter, P. 2017 History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 820, 667–692.CrossRefGoogle Scholar
Castillo, L. & George, W.K. 2001 Similarity analysis for turbulent boundary layer with pressure gradient: outer flow. AIAA J. 39 (1), 41–47.CrossRefGoogle Scholar
Cipolla, K.M. & Keith, W.L. 2003 High Reynolds number thick axisymmetric turbulent boundary layer measurements. Exp. Fluids 35 (5), 477–485.CrossRefGoogle Scholar
Clauser, F.H. 1954 Turbulent boundary layer in adverse pressure gradient. J. Aero. Sci. 21, 91–108.CrossRefGoogle Scholar
de Kat, R. & Ganapathisubramani, B. 2015 Frequency–wavenumber mapping in turbulent shear flows. J. Fluid Mech. 783, 166–190.CrossRefGoogle Scholar
Del Álamo, J.C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor's approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
Dengel, P. & Fernholz, H.H. 1990 An experimental investigation of an incompressible turbulent boundary layer in the vicinity of separation. J. Fluid Mech. 212, 615–636.CrossRefGoogle Scholar
Devenport, W.J., Burdisso, R.A., Borgoltz, A., Ravetta, P.A., Barone, M.F., Brown, K.A. & Morton, M.A. 2013 The Kevlar-walled anechoic wind tunnel. J. Sound Vib. 332 (17), 3971–3991.CrossRefGoogle Scholar
Drozdz, A. & Elsner, W. 2017 Amplitude modulation and its relation to streamwise convection velocity. Intl J. Heat Fluid Flow 63, 67–74.CrossRefGoogle Scholar
Elsberry, K, Loeffler, J, Zhou, M.D. & Wygnanski, I 2000 An experimental study of a boundary layer that is maintained on the verge of separation. J. Fluid Mech. 423, 227–261.CrossRefGoogle Scholar
Glauert, M.B. & Lighthill, M.J. 1955 The axisymmetric boundary layer on a long thin cylinder. Proc. R. Soc. Lond. A 230 (1181), 188–203.Google Scholar
Glegg, S. & Devenport, W. 2017 Aeroacoustics of Low mach Number Flows: Fundamentals, Analysis, and Measurement. Academic Press.Google Scholar
Gungor, A.G., Maciel, Y., Simens, M.P. & Soria, J. 2016 Scaling and statistics of large-defect adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 59, 109–124.CrossRefGoogle Scholar
Hammache, M., Browand, F.K. & Blackwelder, R.F. 2002 Whole-field velocity measurements around an axisymmetric body with a Stratford–Smith pressure recovery. J. Fluid Mech. 461, 1–24.CrossRefGoogle Scholar
Harun, Z., Monty, J.P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.CrossRefGoogle Scholar
Huang, T., Liu, H.L., Groves, N., Forlini, T., Blanton, J. & Gowling, S. 1992 Measurements of flows over an axisymmetric body with various appendages in a wind tunnel: the DARPA SUBOFF experimental program. In Proceedings of the 19th Symposium of Naval HYDRODYNAMICS, Session V, p. 321. National Academy Press.Google Scholar
Hutchins, N., Nickels, T.B., Marusic, I. & Chong, M.S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Jimenez, J.M., Hultmark, M. & Smits, A.J. 2010 The intermediate wake of a body of revolution at high Reynolds numbers. J. Fluid Mech. 659, 516–539.CrossRefGoogle Scholar
Jordan, S.A. 2014 On the axisymmetric turbulent boundary layer growth along long thin circular cylinders. Trans. ASME J. Fluids Engng 136 (5), 051202.CrossRefGoogle Scholar
Kitsios, V., Sekimoto, A., Atkinson, C., Sillero, J.A., Borrell, G., Gungor, A.G., Jiménez, J. & Soria, J. 2017 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer at the verge of separation. J. Fluid Mech. 829, 392–419.CrossRefGoogle Scholar
Kumar, P. & Mahesh, K. 2018 a Analysis of axisymmetric boundary layers. J. Fluid Mech. 849, 927–941.CrossRefGoogle Scholar
Kumar, P. & Mahesh, K. 2018 b Large-eddy simulation of flow over an axisymmetric body of revolution. J. Fluid Mech. 853, 537–563.CrossRefGoogle Scholar
Lee, J.H. 2017 Large-scale motions in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 810, 323–361.CrossRefGoogle Scholar
Lee, J.H., Kevin, , Monty, J.P. & Hutchins, N. 2016 Validating under-resolved turbulence intensities for PIV experiments in canonical wall-bounded turbulence. Exp. Fluids 57 (8), 129.CrossRefGoogle Scholar
Lueptow, R.M., Leehey, P. & Stellinger, T. 1985 The thick, turbulent boundary layer on a cylinder: mean and fluctuating velocities. Phys. Fluids 28 (12), 3495–3505.CrossRefGoogle Scholar
Maciel, Y., Simens, M.P. & Gungor, A.G. 2017 Coherent structures in a non-equilibrium large-velocity-defect turbulent boundary layer. Flow Turbul. Combust. 98 (1), 1–20.CrossRefGoogle Scholar
Maciel, Y., Tie, W., Gungor, A.G. & Simens, M.P. 2018 Outer scales and parameters of adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 844, 5–35.CrossRefGoogle Scholar
Manovski, P., Giacobello, M. & Jacquemin, P. 2014 Smoke flow visualisation and particle image velocimetry measurements over a generic submarine model. Tech. Rep.. Defence Science and Technology Organization (Australia).Google Scholar
Manovski, P., Jones, M.B., Henbest, S.M., Xue, Y., Giacobello, M. & de Silva, C. 2020 Boundary layer measurements over a body of revolution using long-distance particle image velocimetry. Intl J. Heat Fluid Flow 83, 108591.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.CrossRefGoogle Scholar
Michalke, A. 1991 On the instability of wall-boundary layers close to separation. In Separated Flows and Jets (ed. V.V. Kozlov & A.V. Dovgal), pp. 557–564. Springer Berlin Heidelberg.CrossRefGoogle Scholar
Morton, M.A., Devenport, W.J. & Glegg, S. 2012 Rotor inflow noise caused by a boundary layer: inflow measurements and noise predictions. In 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), p. 2120. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Nagano, Y., Tsuji, T. & Houra, T. 1998 Structure of turbulent boundary layer subjected to adverse pressure gradient. Intl J. Heat Fluid Flow 19 (5), 563–572.CrossRefGoogle Scholar
Neves, J.C., Moin, P. & Moser, R.D. 1994 Effects of convex transverse curvature on wall-bounded turbulence. Part 1. The velocity and vorticity. J. Fluid Mech. 272, 349–382.CrossRefGoogle Scholar
Oster, D. & Wygnanski, I. 1982 The forced mixing layer between parallel streams. J. Fluid Mech. 123, 91–130.CrossRefGoogle Scholar
Patel, V.C., Nakayama, A & Damian, R 1974 Measurements in the thick axisymmetric turbulent boundary layer near the tail of a body of revolution. J. Fluid Mech. 63 (2), 345–367.CrossRefGoogle Scholar
Piquet, J. & Patel, V.C. 1999 Transverse curvature effects in turbulent boundary layer. Prog. Aero. Sci. 35 (7), 661–672.CrossRefGoogle Scholar
Pope, S.B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Raffel, M., Willert, C.E., Scarano, F., Káhler, C.J., Wereley, S.T. & Kompenhans, J. 2018 Particle image velocimetry: a practical guide. Springer.CrossRefGoogle Scholar
Rao, G.N.V. 1967 The law of the wall in a thick axisymmetric turbulent boundary layer. J. Appl. Mech. 34 (1), 237–238.CrossRefGoogle Scholar
Renard, N. & Deck, S. 2015 On the scale-dependent turbulent convection velocity in a spatially developing flat plate turbulent boundary layer at Reynolds number $Re_{\theta }=13\,000$. J. Fluid Mech. 775, 105–148.CrossRefGoogle Scholar
Schatzman, D.M. & Thomas, F.O. 2017 An experimental investigation of an unsteady adverse pressure gradient turbulent boundary layer: embedded shear layer scaling. J. Fluid Mech. 815, 592–642.CrossRefGoogle Scholar
Schetz, J.A & Bowersox, R.D.W. 2011 Boundary layer analysis. American Institute of Aeronautics and Astronautics.Google Scholar
Skåre, P.E. & Krogstad, P. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.CrossRefGoogle Scholar
Snarski, S.R. & Lueptow, R.M. 1995 Wall pressure and coherent structures in a turbulent boundary layer on a cylinder in axial flow. J. Fluid Mech. 286, 137–171.CrossRefGoogle Scholar
Song, S., DeGraaff, D.B. & Eaton, J.K. 2000 Experimental study of a separating, reattaching, and redeveloping flow over a smoothly contoured ramp. Intl J. Heat Fluid Flow 21 (5), 512–519.CrossRefGoogle Scholar
Taylor, G.I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164 (919), 476–490.CrossRefGoogle Scholar
Tutkun, M., George, W.K., Delville, J., Stanislas, M., Johansson, P.B.V., Foucaut, J.M. & Coudert, S. 2009 Two-point correlations in high Reynolds number flat plate turbulent boundary layers. J. Turbul. 10, N21.CrossRefGoogle Scholar
Tutty, O.R. 2008 Flow along a long thin cylinder. J. Fluid Mech. 602, 1–37.CrossRefGoogle Scholar
Tutu, N.K. & Chevray, R. 1975 Cross-wire anemometry in high intensity turbulence. J. Fluid Mech. 71 (4), 785–800.CrossRefGoogle Scholar
Vila, C.S., Örlü, R., Vinuesa, R., Schlatter, P., Ianiro, A. & Discetti, S. 2017 Adverse-pressure-gradient effects on turbulent boundary layers: statistics and flow-field organization. Flow Turbul. Combust. 99 (3–4), 589–612.CrossRefGoogle Scholar
Wittmer, K.S., Devenport, W.J. & Zsoldos, J.S. 1998 A four-sensor hot-wire probe system for three-component velocity measurement. Exp. Fluids 24 (5), 416–423.CrossRefGoogle Scholar
Wygnanski, I., Champagne, F. & Marasli, B. 1986 On the large-scale structures in two-dimensional, small-deficit, turbulent wakes. J. Fluid Mech. 168, 31–71.CrossRefGoogle Scholar
Zagarola, M.V. & Smits, A.J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar
Zhou, D., Wang, K. & Wang, M. 2020 Large-eddy simulation of an axisymmetric boundary layer on a body of revolution. In AIAA Aviation 2020 Forum, p. 2989. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar