Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kunnen, Rudie P. J.
Corre, Yoann
and
Clercx, Herman J. H.
2013.
Vortex plume distribution in confined turbulent rotating convection.
EPL (Europhysics Letters),
Vol. 104,
Issue. 5,
p.
54002.
Horn, Susanne
and
Shishkina, Olga
2014.
Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water.
Physics of Fluids,
Vol. 26,
Issue. 5,
Gutierrez-Castillo, Paloma
and
Lopez, Juan M.
2015.
Instabilities of the sidewall boundary layer in a rapidly rotating split cylinder.
European Journal of Mechanics - B/Fluids,
Vol. 52,
Issue. ,
p.
76.
Horn, Susanne
and
Shishkina, Olga
2015.
Toroidal and poloidal energy in rotating Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 762,
Issue. ,
p.
232.
Calkins, Michael A.
Hale, Kevin
Julien, Keith
Nieves, David
Driggs, Derek
and
Marti, Philippe
2015.
The asymptotic equivalence of fixed heat flux and fixed temperature thermal boundary conditions for rapidly rotating convection.
Journal of Fluid Mechanics,
Vol. 784,
Issue. ,
Rajaei, Hadi
Joshi, Pranav
Alards, Kim M. J.
Kunnen, Rudie P. J.
Toschi, Federico
and
Clercx, Herman J. H.
2016.
Transitions in turbulent rotating convection: A Lagrangian perspective.
Physical Review E,
Vol. 93,
Issue. 4,
Sterl, Sebastian
Li, Hui-Min
and
Zhong, Jin-Qiang
2016.
Dynamical and statistical phenomena of circulation and heat transfer in periodically forced rotating turbulent Rayleigh-Bénard convection.
Physical Review Fluids,
Vol. 1,
Issue. 8,
Horn, Susanne
and
Schmid, Peter J.
2017.
Prograde, retrograde, and oscillatory modes in rotating Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
182.
Lemasquerier, D.
Grannan, A. M.
Vidal, J.
Cébron, D.
Favier, B.
Le Bars, M.
and
Aurnou, J. M.
2017.
Libration‐driven flows in ellipsoidal shells.
Journal of Geophysical Research: Planets,
Vol. 122,
Issue. 9,
p.
1926.
Liu, Wenjun
Krasnov, Dmitry
and
Schumacher, Jörg
2018.
Wall modes in magnetoconvection at high Hartmann numbers.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
Cheng, Jonathan S.
Aurnou, Jonathan M.
Julien, Keith
and
Kunnen, Rudie P. J.
2018.
A heuristic framework for next-generation models of geostrophic convective turbulence.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 112,
Issue. 4,
p.
277.
Plumley, Meredith
and
Julien, Keith
2019.
Scaling Laws in Rayleigh‐Bénard Convection.
Earth and Space Science,
Vol. 6,
Issue. 9,
p.
1580.
Horn, Susanne
and
Aurnou, Jonathan M.
2019.
Rotating convection with centrifugal buoyancy: Numerical predictions for laboratory experiments.
Physical Review Fluids,
Vol. 4,
Issue. 7,
Rodríguez-García, J. O.
and
Burguete, J.
2019.
Experimental lateral wall boundary layer behavior of a differentially rotating split-cylinder flow.
Physical Review E,
Vol. 99,
Issue. 2,
de Wit, Xander M.
Aguirre Guzmán, Andrés J.
Madonia, Matteo
Cheng, Jonathan S.
Clercx, Herman J. H.
and
Kunnen, Rudie P. J.
2020.
Turbulent rotating convection confined in a slender cylinder: The sidewall circulation.
Physical Review Fluids,
Vol. 5,
Issue. 2,
Zhang, Xuan
van Gils, Dennis P. M.
Horn, Susanne
Wedi, Marcel
Zwirner, Lukas
Ahlers, Guenter
Ecke, Robert E.
Weiss, Stephan
Bodenschatz, Eberhard
and
Shishkina, Olga
2020.
Boundary Zonal Flow in Rotating Turbulent Rayleigh-Bénard Convection.
Physical Review Letters,
Vol. 124,
Issue. 8,
Yang, Yantao
Verzicco, Roberto
Lohse, Detlef
and
Stevens, Richard J. A. M.
2020.
What rotation rate maximizes heat transport in rotating Rayleigh-Bénard convection with Prandtl number larger than one?.
Physical Review Fluids,
Vol. 5,
Issue. 5,
Vogt, Tobias
Horn, Susanne
and
Aurnou, Jonathan M.
2021.
Oscillatory thermal–inertial flows in liquid metal rotating convection.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
Horn, Susanne
and
Aurnou, Jonathan M.
2021.
Tornado-like vortices in the quasi-cyclostrophic regime of Coriolis-centrifugal convection.
Journal of Turbulence,
Vol. 22,
Issue. 4-5,
p.
297.
Kunnen, Rudie P. J.
2021.
The geostrophic regime of rapidly rotating turbulent convection.
Journal of Turbulence,
Vol. 22,
Issue. 4-5,
p.
267.
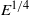 ${E}^{1/ 4} $ and
${E}^{1/ 4} $ and 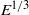 ${E}^{1/ 3} $, where
${E}^{1/ 3} $, where 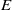 $E$ is the Ekman number. Although the structure of the bulk-driven circulation may change considerably depending on the Ekman number, the boundary-layer recirculation is present at all Ekman numbers in the range
$E$ is the Ekman number. Although the structure of the bulk-driven circulation may change considerably depending on the Ekman number, the boundary-layer recirculation is present at all Ekman numbers in the range 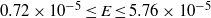 $0. 72\times 1{0}^{- 5} \leq E\leq 5. 76\times 1{0}^{- 5} $ considered here.
$0. 72\times 1{0}^{- 5} \leq E\leq 5. 76\times 1{0}^{- 5} $ considered here.

