Published online by Cambridge University Press: 03 July 2013
This paper describes an investigation of the linear, diffusive critical layer for shear flows whose inviscid neutral modes have an algebraic branch point. As examples of flows exhibiting such singular behaviour, we treat both stratified shear flows and non-axisymmetric modes on vortices. For the stratified case, the coupled vorticity and energy equations are solved numerically. In this way, the density perturbation, which is unbounded in the absence of diffusion, is determined directly. As an example featuring a vortex, we consider helical modes on a modified Lamb–Oseen vortex whose velocity profile is perturbed in such a way that linear instability is possible. Both the axial and azimuthal velocity perturbations in the critical layer are determined. A characteristic shared by all the above problems is that they involve eigenfunctions that are oscillatory in some region. For forced waves in a stably stratified shear flow, we consider a larger range of parameters than previous investigators. We also examine some experiments and find that the Reynolds stress is sensitive to the actual density profile in the region between a wavy wall providing the forcing and the critical layer. For the stratified shear flows without forcing, much smaller Richardson numbers are involved and the modes considered are over-reflecting. For an unbounded 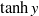 $\tanh y$ mixing layer, we show that the Reynolds stress for a neutral mode must jump across the critical layer. With the presence of a horizontal boundary beneath the shear layer, on the other hand, over-reflection can occur, with the Reynolds stress vanishing on either side of the critical layer. In all cases, the variation of the Reynolds stress across the critical layer is determined.
$\tanh y$ mixing layer, we show that the Reynolds stress for a neutral mode must jump across the critical layer. With the presence of a horizontal boundary beneath the shear layer, on the other hand, over-reflection can occur, with the Reynolds stress vanishing on either side of the critical layer. In all cases, the variation of the Reynolds stress across the critical layer is determined.