Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T07:38:42.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Subcritical bifurcation of shear-thinning plane Poiseuille flows

Published online by Cambridge University Press:  29 September 2011

A. Chekila ,
C. Nouar ,
E. Plaut  and
A. Nemdili
A. Chekila
Affiliation:
Laboratoire de Rhéologie, Faculté de Génie Mécanique, Université des Sciences et de la Technologie d’Oran, B.P. 1505 El M’Naouer Oran 31000, Algeria LEMTA, UMR 7563 (CNRS – Nancy Université), 2 Avenue de la Forêt de Haye, BP 160, 54504 Vandoeuvre CEDEX, France
C. Nouar*
Affiliation:
LEMTA, UMR 7563 (CNRS – Nancy Université), 2 Avenue de la Forêt de Haye, BP 160, 54504 Vandoeuvre CEDEX, France
E. Plaut
Affiliation:
LEMTA, UMR 7563 (CNRS – Nancy Université), 2 Avenue de la Forêt de Haye, BP 160, 54504 Vandoeuvre CEDEX, France
A. Nemdili
Affiliation:
Laboratoire de Rhéologie, Faculté de Génie Mécanique, Université des Sciences et de la Technologie d’Oran, B.P. 1505 El M’Naouer Oran 31000, Algeria
*
†Email address for correspondence: cherif.nouar@ensem.inpl-nancy.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In a recent article (Nouar, Bottaro & Brancher, J. Fluid. Mech., vol. 592, 2007, pp. 177–194), a linear stability analysis of plane Poiseuille flow of shear-thinning fluids has been performed. The authors concluded that the viscosity stratification delays the transition and that is important to account for the viscosity perturbation. 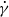The current paper focuses on the first-principles understanding of the influence of the viscosity stratification and the nonlinear variation of the effective viscosity with the shear rate on the flow stability with respect to a finite-amplitude perturbation. A weakly nonlinear analysis, using the amplitude expansion method, is adopted as a first approach to study nonlinear effects. The bifurcation to two-dimensional travelling waves is studied. For the numerical computations, the shear-thinning behaviour is described by the Carreau model. The rheological parameters are varied in a wide range. The results indicate that (i) the nonlinearity of the viscous terms tends to reduce the viscous dissipation and to accelerate the flow, (ii) the harmonic generated by the nonlinearity 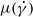is smaller and in opposite phase to that generated by the quadratic nonlinear inertial terms and (iii) with increasing shear-thinning effects, the bifurcation becomes highly subcritical. Consequently, the magnitude of the threshold amplitude of the perturbation, beyond which the flow is nonlinearly unstable, decreases. This result is confirmed by computing higher order-Landau constants.

JFM classification

Waves/Free-surface Flows: Channel flow Instability: Nonlinear instability Non-Newtonian Flows: Non-Newtonian Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 686 , 10 November 2011 , pp. 272 - 298
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Albbalbaki, B. & Khayat, R. E. 2011 Pattern selection in the thermal convection of non-Newtonian fluids. J. Fluid Mech. 668, 500–550.CrossRefGoogle Scholar
2. Balmforth, N. J. & Rust, A. C. 2009 Weakly nonlinear viscoplastic convection. J. Non-Newtonian Fluid Mech. 158, 36–45.CrossRefGoogle Scholar
3. Billingham, J. & Ferguson, J. W. J. 1993 Laminar, unidirectional flow of a thixotropic fluid in a circular pipe. J. Non-Newtonian Fluid Mech. 47, 21–55.CrossRefGoogle Scholar
4. Bird, R., Amstrong, R. & Hassager, O. 1987 Dynamics of Polymeric Liquids. Wiley Interscience.Google Scholar
5. Carreau, J. P. 1972 Rheological equations from molecular network theories. J. Rheol. 16, 99–127.Google Scholar
6. Chikkadi, V., Sameen, A. & Govindarajan, R. 2005 Preventing transition to turbulence: a viscosity stratification does not always help. Phys. Rev. Lett. 95, 264504.1–4.CrossRefGoogle Scholar
7. Drazin, P. G. & Reid, W. H. 1995 Hydrodynamic Stability. Cambridge University Press.Google Scholar
8. Ern, P., Charru, F. & Luchini, P. 2003 Stability analysis of a shear flow with strongly stratified viscosity. J. Fluid Mech. 496, 295–312.CrossRefGoogle Scholar
9. Fujimura, K. 1989 The equivalence between two perturbation methods in weakly nonlinear stability theory for parallel shear flows. Proc. R. Soc. Lond. A 424, 373–392.Google Scholar
10. Govindarajan, R. 2002 Surprising effects of minor viscosity gradients. J. Indian Inst. Sci. 82, 121–127.Google Scholar
11. Govindarajan, R., L’vov, V. S. & Proccaccia, I. 2001 Retardation of the onset of turbulence by minor viscosity contrasts. Phys. Rev. Lett. 87, 174501.1–4.CrossRefGoogle ScholarPubMed
12. Govindarajan, R., L’Vov, V. S., Procaccia, I. & Sameen, A. 2003 Stabilization of hydrodynamic flows by small viscosity variations. Phys. Rev. E 67, 026310.1–11.CrossRefGoogle ScholarPubMed
13. Herbert, T. 1980 Nonlinear stability of parallel flows by high-order amplitude expansions. AIAA J. 18, 243–248.CrossRefGoogle Scholar
14. Herbert, T. 1983 On perturbation methods in nonlinear stability theory. J. Fluid Mech. 126, 167–186.CrossRefGoogle Scholar
15. Nouar, C., Bottaro, A. & Brancher, J. P. 2007 Delaying transition to turbulence in channel flow: revisiting the stability of shear-thinning fluids. J. Fluid. Mech. 592, 177–194.CrossRefGoogle Scholar
16. Nouar, C. & Frigaard, I. 2009 Stability of plane Couette–Poiseuille flow of shear-thinning fluid. Phys. Fluids 21, 064104.1–13.CrossRefGoogle Scholar
17. Phillips, G. O. & Williams, P. A. 2000 Handbook of Hydrocolloïdes. Woodhead Publishing.Google Scholar
18. Plaut, E., Lebranchu, Y., Simitev, R. & Busse, F. H. 2008 Reynolds stresses and mean fields generated by pure waves: applications to shear flows and convection in a rotating cell. J. Fluid Mech. 602, 303–326.CrossRefGoogle Scholar
19. Quemada, D. 1978 Rheology of concentrated disperse sytem. ii. A model for non-Newtonian shear viscosity in steady flows. Rheol. Acta 17, 632–642.CrossRefGoogle Scholar
20. Ranganathan, B. T. & Govindarajan, R. 2001 Stabilization and destabilization of channel flow by location of viscosity-stratified fluid layer. Phy. Fluids 13, 1–3.CrossRefGoogle Scholar
21. Reynolds, W. C. & Potter, M. C. 1967 Finite-amplitude instability of parallel shear flows. J. Fluid Mech. 27, 465–492.CrossRefGoogle Scholar
22. Sameen, A. & Govindarajan, R. 2007 The effect of wall heating on instability of channel flow. J. Fluid Mech. 577, 417–442.CrossRefGoogle Scholar
23. Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
24. Stuart, J. T. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows: Part 1. The basic behaviour in plane Poiseuille flow. J. Fluid Mech. 9, 353–370.CrossRefGoogle Scholar
25. Tanner, R. 2000 Engineering Rheology. Oxford University Press.CrossRefGoogle Scholar
26. Trefethen, L. N. 2008 Is Gauss quadrature better than Clenshaw–Curtis? SIAM Rev. 50, 67–87.CrossRefGoogle Scholar
27. Wall, D. P. & Wilson, S. K. 1996 The linear stability of channel flow of fluid with temperature-dependent viscosity. J. Fluid Mech. 323, 107–132.CrossRefGoogle Scholar
28. Watson, J. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. Part 2. The development of a solution for plane Poiseuille and for plane Couette flow. J. Fluid Mech. 9, 371–389.CrossRefGoogle Scholar