Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T15:53:32.935Z Has data issue: false hasContentIssue false
  • English
  • Français

Superhydrophobic surface immobilisation by insoluble surfactant

Published online by Cambridge University Press:  28 September 2022

Michael D. Mayer Open the ORCID record for Michael D. Mayer [Opens in a new window]  and
Darren G. Crowdy Open the ORCID record for Darren G. Crowdy [Opens in a new window]
Michael D. Mayer*
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen's Gate, London SW7 2AZ, UK
Darren G. Crowdy
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen's Gate, London SW7 2AZ, UK
*
†Email address for correspondence: m.mayer@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

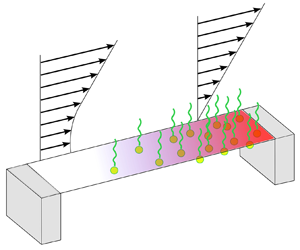
The effects of insoluble surfactants, satisfying a Langmuir equation of state, on transverse Stokes flow over a superhydrophobic surface of unidirectional grooves with flat menisci are examined. The phenomenon of surface immobilisation, whereby surfactants cause part or all of the Cassie-state menisci to become effectively no-slip zones thereby degrading the slip properties of the surface, is of primary interest. The study employs a combined analytical and numerical approach allowing an exploration of surfactant effects over the full range of surface Péclet numbers, Marangoni numbers and surfactant loads. For small surface Péclet and Marangoni numbers, perturbation theory is used to gain basic insights into the physical mechanisms at work. That analysis also provides checks on a robust numerical scheme, built around a complex variable formulation of the problem, used to compute solutions across a wide range of non-dimensional parameter values. Two distinct mechanisms are found to be responsible for surface immobilisation. In the first, most commonly seen at higher surface Péclet numbers, a stagnant cap forms because swept surfactant immobilises a section of the meniscus before any portion of the meniscus reaches maximum packing. Such a cap exists even for a linear equation of state and grows in length with increasing Marangoni number. A second immobilisation mechanism is associated with the nonlinear equation of state: an immobilised region forms because the surfactant concentration reaches its maximum value near the downstream edge of the meniscus. Immobilisation of the latter form can occur at much lower surface Péclet numbers, even if the Marangoni number is small, as long as there is sufficient surfactant in the system. The study enhances understanding of how insoluble surfactants can degrade slip over superhydrophobic surfaces.

JFM classification

Flow Control: Drag reduction Mass Transport: Coupled diffusion and flow Convection: Marangoni convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 949 , 25 October 2022 , A18
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anna, S.L. & Mayer, H.C. 2006 Microscale tipstreaming in a microfluidic flow focusing device. Phys. Fluids 18 (12), 121512.CrossRefGoogle Scholar
Baier, T. & Hardt, S. 2021 Influence of insoluble surfactants on shear flow over a surface in Cassie state at large Péclet numbers. J. Fluid Mech. 907, A3.CrossRefGoogle Scholar
Bolognesi, G., Cottin-Bizonne, C. & Pirat, C. 2014 Evidence of slippage breakdown for a superhydrophobic microchannel. Phys. Fluids 26, 082004.CrossRefGoogle Scholar
Crowdy, D.G. 2011 Frictional slip lengths for unidirectional superhydrophobic grooved surfaces. Phys. Fluids 23, 072001.CrossRefGoogle Scholar
Crowdy, D.G. 2013 Surfactant-induced stagnant zones in the Jeong-Moffatt free surface Stokes flow problem. Phys. Fluids 25, 092104.CrossRefGoogle Scholar
Crowdy, D.G. 2017 a Effective slip lengths for immobilized superhydrophobic surfaces. J. Fluid Mech. 825, R2.CrossRefGoogle Scholar
Crowdy, D.G. 2017 b Perturbation analysis of subphase gas and meniscus curvature effects for longitudinal flows over superhydrophobic surfaces. J. Fluid Mech. 822, 307–326.CrossRefGoogle Scholar
Crowdy, D.G. 2020 a Collective viscous propulsion of a two-dimensional flotilla of Marangoni boats. Phys. Rev. Fluids 5, 124004.CrossRefGoogle Scholar
Crowdy, D.G. 2020 b Solving Problems in Multiply Connected Domains. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Crowdy, D.G. 2021 Slip length formulas for longitudinal shear flow over a superhydrophobic grating with partially filled cavities. J. Fluid Mech. 925, R2.CrossRefGoogle Scholar
Cuenot, B., Magnaudet, J. & Spennato, B. 1997 The effects of slightly soluble surfactants on the flow around a spherical bubble. J. Fluid Mech. 339, 25–53.CrossRefGoogle Scholar
Davis, R.E. & Acrivos, A. 1966 The influence of surfactants on the creeping motion of bubbles. Chem. Engng Sci. 21, 681–685.CrossRefGoogle Scholar
Halpern, D. & Frenkel, A.L. 2003 Destabilization of a creeping flow by interfacial surfactant: linear theory extended to all wavenumbers. J. Fluid Mech. 485, 191–220.CrossRefGoogle Scholar
He, Z., Maldarelli, C. & Dagan, Z. 1991 Evidence of slippage breakdown for a superhydrophobic microchannel. J. Colloid Interface Sci. 146, 442–451.CrossRefGoogle Scholar
Kirk, T.L. 2018 Asymptotic formulae for flow in superhydrophobic channels with longitudinal ridges and protruding menisci. J. Fluid Mech. 839, R3.CrossRefGoogle Scholar
Landel, J.R., Peaudecerf, F.J., Temprano-Coleto, F., Gibou, F. & Goldstein, R.E. 2020 A theory for the slip and drag of superhydrophobic surfaces with surfactant. J. Fluid Mech. 883, A18.CrossRefGoogle ScholarPubMed
Lee, C., Choi, C.H. & Kim, C.J. 2016 Superhydrophobic drag reduction in laminar flows: a critical review. Exp. Fluids 57, 176.CrossRefGoogle Scholar
Levich, V. 1962 Physicochemical Hydrodynamics. Prentice Hall.Google Scholar
Palaparthi, R., Papageorgiou, D.T. & Maldarelli, C. 2006 Theory and experiments on the stagnant cap regime in the motion of spherical surfactant-laden bubbles. J. Fluid Mech. 559, 1–44.CrossRefGoogle Scholar
Peaudecerf, F.J., Landel, J.R., Goldstein, R.E. & Luzzatto-Fegiz, P. 2017 Traces of surfactants can severely limit the drag reduction of superhydrophobic surfaces. Proc. Natl Acad. Sci. 114, 7254–7259.CrossRefGoogle ScholarPubMed
Philip, J.R. 1972 Flows satisfying mixed no-slip and no-shear conditions. J. Appl. Math. Phys. 23, 353–372.Google Scholar
Pozrikidis, C. 2010 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Rothstein, J.P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 109, 42–89.Google Scholar
Sadhal, S.S. & Johnson, R.E. 1983 Stokes flow past bubbles and drops partially coated with thin films I: stagnant cap of surfactant film-exact solution. J. Fluid Mech. 126, 237–250.CrossRefGoogle Scholar
Savic, P. 1953 Circulation and distortion of liquid drops falling through a viscous medium. Tech. Rep. MT-22. Division of Mechanical Engineering, National Research Council Canada.Google Scholar
Siegel, M.I. 1999 Influence of surfactant on rounded and pointed bubbles in two-dimensional Stokes flow. SIAM J. Appl. Maths 59, 1998–2027.CrossRefGoogle Scholar
Wang, Y., Papageorgiou, D.T. & Maldarelli, C. 1999 Increased mobility of a surfactant-retarded bubble at high bulk concentrations. J. Fluid Mech. 390, 251–270.CrossRefGoogle Scholar
Wang, Y., Papageorgiou, D.T. & Maldarelli, C. 2002 Using surfactants to control the formation and size of wakes behind moving bubbles at order-one Reynolds numbers. J. Fluid Mech. 453, 1–19.CrossRefGoogle Scholar