Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T08:06:50.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Supersonic cylinder wake dynamics

Published online by Cambridge University Press:  14 July 2022

M. Awasthi Open the ORCID record for M. Awasthi [Opens in a new window] ,
S. McCreton Open the ORCID record for S. McCreton [Opens in a new window] ,
D.J. Moreau Open the ORCID record for D.J. Moreau [Opens in a new window]  and
C.J. Doolan Open the ORCID record for C.J. Doolan [Opens in a new window]
M. Awasthi*
Affiliation:
School of Mechanical and Manufacturing Engineering, University of New South Wales, Sydney 2052, Australia
S. McCreton
Affiliation:
School of Mechanical and Manufacturing Engineering, University of New South Wales, Sydney 2052, Australia
D.J. Moreau
Affiliation:
School of Mechanical and Manufacturing Engineering, University of New South Wales, Sydney 2052, Australia
C.J. Doolan
Affiliation:
School of Mechanical and Manufacturing Engineering, University of New South Wales, Sydney 2052, Australia
*
†Email address for correspondence: m.awasthi@unsw.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

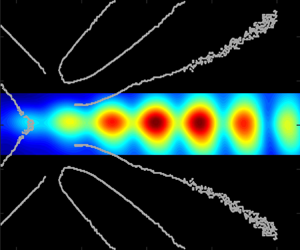
The supersonic wake of a circular cylinder in Mach 3 flow was studied through high-speed, focussing schlieren photography. The mean and unsteady behaviour of the separated shear layers, the reattachment process, the recompression wave and the early wake are analysed, and discussed in detail. The fluctuations in the wake are stronger and more coherent than those within the approaching shear layers and the recirculation region. The recompression of the shear layers energises the finer scales in the flow which leads to a departure from a $-$1 spectral roll-off observed in the schlieren spectra further upstream. The recompression wave exhibits low-frequency unsteadiness and a ripple-type motion which occurs as it is perturbed by shocklets radiating from the coherent structures in the wake. The wake consists of coherent disturbances with the same characteristic frequency as that for an incompressible flow over a cylinder; however, this instability is suppressed as the wake accelerates, presumably due to increasing compressibility. The primary instability of the wake flow has a characteristic frequency nearly twice that of its incompressible counterpart and it is shown to be driven by the presence of aeroacoustic resonance in the wake. It is also shown that the resonance, which leads to the formation of broadband standing waves in the wake, is the result of an interaction between the wake instabilities and upstream propagating acoustic waves in the wake. The acoustic waves originate upstream of the reattachment region and are believed to be generated by the unsteady separation on the cylinder surface.

JFM classification

Acoustics: Aeroacoustics Compressible Flows: Supersonic flow Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 945 , 25 August 2022 , A4
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Amatucci, V.A., Dutton, J.C., Kuntz, D.W. & Addy, A.L. 1992 Two-stream, supersonic, wake flowfield behind a thick base. I – general features. AIAA J. 30 (8), 2039–2046.CrossRefGoogle Scholar
Bailly, C. & Fujii, K. 2016 High-speed jet noise. Mech. Engng Rev. 3 (1), 15-00496.CrossRefGoogle Scholar
Bashkin, V.A., Egorov, I.V., Egorova, M.V. & Ivanov, D.V. 1998 Inititation and development of separated flow behind a circular cylinder in supersonic stream. Fluid Dyn. 33 (6), 833–841.CrossRefGoogle Scholar
Bashkin, V.A., Egorov, I.V., Egorova, M.V. & Ivanov, D.V. 2000 Supersonic laminar-turbulent gas flow past a circular cylinder. Fluid Dyn. 35 (5), 652–662.CrossRefGoogle Scholar
Bashkin, V.A., Vaganov, A.V., Egorov, I.V., Ivanov, D.V. & Ignatova, G.A. 2002 Comparison of calculated and experimental data on supersonic flow past a circular cylinder. Fluid Dyn. 37 (3), 473–483.CrossRefGoogle Scholar
Bogey, C. & Gojon, R. 2017 Feedback loop and upwind-propagating waves in ideally expanded supersonic impinging round jets. J. Fluid Mech. 823, 562–591.CrossRefGoogle Scholar
Bonnet, J.P., Jayaraman, V. & Alziary De Roquefort, T. 1984 Structure of a high-Reynolds-number turbulent wake in supersonic flow. J. Fluid Mech. 143, 277–304.CrossRefGoogle Scholar
Clemens, N.T. & Mungal, M.G. 1992 Two- and three-dimensional effects in the supersonic mixing layer. AIAA J. 30 (4), 973–981.CrossRefGoogle Scholar
Clemens, N.T. & Smith, M.F. 1998 Observations of supersonic flat plate wake transition. AIAA J. 36 (7), 1328–1330.CrossRefGoogle Scholar
Edgington-Mitchell, D., Jaunet, V., Jordan, P., Towne, A., Soria, J. & Honnery, D. 2018 Upstream-travelling acoustic jet modes as a closure mechanism for screech. J. Fluid Mech. 855, R1.CrossRefGoogle Scholar
Edgington-Mitchell, D., Wang, T., Nogueira, P., Schmidt, O., Jaunet, V., Duke, D., Jordan, P. & Towne, A. 2021 Waves in screeching jets. J. Fluid Mech. 913, A7.CrossRefGoogle Scholar
Fujii, K., Nonomura, T. & Tsutsumi, S. 2010 Toward accurate simulation and analysis of strong acoustic wave phenomena-a review from the experience of our study on rocket problems. Intl J. Numer. Meth. Fluids 64 (10–12), 1412–1432.CrossRefGoogle Scholar
Gai, S.L., Hughes, D.P. & Perry, M.S. 2002 Large-scale structures and growth of a flat plate compressible wake. AIAA J. 40 (6), 1164–1169.CrossRefGoogle Scholar
Gang, D., Yi, S. & Niu, H. 2021 Experimental investigation of supersonic turbulent flow over cylinders with various heights. J. Vis. (Visualization) 24 (3), 461–470.CrossRefGoogle Scholar
Garg, S. & Settles, G.S. 1998 Measurements of a supersonic turbulent boundary layer by focusing schlieren deflectometry. Exp. Fluids 25 (3), 254–264.CrossRefGoogle Scholar
Gowen, F.E. & Perkins, E.W. 1953 Drag of circular cylinders for a wide range of Reynolds numbers and Mach numbers. NACA Tech. Rep. National Advisory Committee for Aeronautics, NACA TN 2960.Google Scholar
Harris, P. & Fasel, H. 1996 Numerical investigation of unsteady plane wakes at supersonic speeds. In 34th Aerospace Sciences Meeting and Exhibit. AIAA.CrossRefGoogle Scholar
Harris, P. & Fasel, H. 1998 Numerical investigation of the unsteady behavior of supersonic plane wakes. In 29th AIAA, Fluid Dynamics Conference. AIAA.CrossRefGoogle Scholar
Hickey, J.-P., Hussain, F. & Wu, X. 2016 Compressibility effects on the structural evolution of transitional high-speed planar wakes. J. Fluid Mech. 796, 5–39.CrossRefGoogle Scholar
Humble, R.A., Scarano, F. & van Oudheusden, B.W. 2007 Unsteady flow organization of compressible planar base flows. Phys. Fluids 19 (7), 076101.CrossRefGoogle Scholar
Kuntz, D.W., Amatucci, V.A. & Addy, A.L. 1987 Turbulent boundary-layer properties downstream of the shock-wave/boundary-layer interaction. AIAA J. 25 (5), 668–675.CrossRefGoogle Scholar
Lachney, E.R. & Clemens, N.T. 1998 Plif imaging of mean temperature and pressure in a supersonic bluff wake. Exp. Fluids 24, 354–363.CrossRefGoogle Scholar
Lawson, M., Hargather, M., Settles, G., Weinstein, W. & Gogineni, S. 2009 Focusing-schlieren PIV measurements of a supersonic turbulent boundary layers. In 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. AIAA.CrossRefGoogle Scholar
Li, Q. 2022 Analysis of the dynamic characteristics in the supersonic wake using dynamic mode decomposition. J. Braz. Soc. Mech. Sci. Engng 44 (4), 137.CrossRefGoogle Scholar
Lysenko, V.I. 1999 Experimental studies of stability and transition in high-speed wakes. J. Fluid Mech. 392, 1–26.CrossRefGoogle Scholar
Ma, X., Karamanos, G.S. & Karniadakis, G.E. 2000 Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 410, 29–65.CrossRefGoogle Scholar
Martinez-Gonzalez, A., Moreno-Hernandez, D., Guerrero-Viramontes, J.A., Leon- Rodriguez, M., Zamarripa-Ramirez, J.C.I. & Carrillo-Delgado, C. 2018 Temperature measurement of fluid flows by using a focusing schlieren method. Sensors (Basel) 19 (1), 12.CrossRefGoogle ScholarPubMed
Murthy, V. & Rose, W. 1977 Form drag, skin friction, and vortex shedding frequencies for subsonic and transonic crossflows on circular cylinder. In 10th Fluid and Plasmadynamics Conference.CrossRefGoogle Scholar
Nonomura, T. & Fujii, K. 2011 Overexpansion effects on characteristics of mach waves from a supersonic cold jet. AIAA J. 49 (10), 2282–2294.CrossRefGoogle Scholar
Panda, J. 1999 An experimental investigation of screech noise generation. J. Fluid Mech. 378, 71–96.CrossRefGoogle Scholar
Papamoschou, D. & Roshko, A. 2006 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.CrossRefGoogle Scholar
Paris, S., Hasinoff, S.W. & Kautz, J. 2015 Local Laplacian filters: edge-aware image processing with a Laplacian pyramid. Commun. ACM 58 (3), 81–91.CrossRefGoogle Scholar
Passmann, M., aus der Wiesche, S. & Joos, F. 2020 Focusing schlieren visualization of transonic turbine tip-leakage flows. Intl J. Turbomach. Propul. Power 5 (1), 1.CrossRefGoogle Scholar
Poggie, J. & Smits, A.J. 2001 Shock unsteadiness in a reattaching shear layer. J. Fluid Mech. 429, 155–185.CrossRefGoogle Scholar
Sandberg, R.D. 2012 Numerical investigation of turbulent supersonic axisymmetric wakes. J. Fluid Mech. 702, 488–520.CrossRefGoogle Scholar
Sandham, N.D. & Reynolds, W.C. 2006 Three-dimensional simulations of large eddies in the compressible mixing layer. J. Fluid Mech. 224, 133–158.CrossRefGoogle Scholar
Scarano, F. & Oudheusden, B.W. 2003 Planar velocity measurements of a two-dimensional compressible wake. Exp. Fluids 34 (3), 430–441.CrossRefGoogle Scholar
Schmidt, B.E. & Shepherd, J.E. 2015 Oscillations in cylinder wakes at Mach 4. J. Fluid Mech. 785, R3.CrossRefGoogle Scholar
Simon, F., Deck, S., Guillen, P., Sagaut, P. & Merlen, A. 2007 Numerical simulation of the compressible mixing layer past an axisymmetric trailing edge. J. Fluid Mech. 591, 215–253.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures, parts I–III. Q. Appl. Maths 45 (3), 561–571.CrossRefGoogle Scholar
Smith, K. & Dutton, J. 1995 Large-scale structures in supersonic reattaching shear flows. In AIAA Fluid Dynamics Conference. AIAA.CrossRefGoogle Scholar
Smith, K.M. & Dutton, J.C. 1996 Investigation of large-scale structures in supersonic planar base flows. AIAA J. 34 (6), 1146–1152.CrossRefGoogle Scholar
Smits, A. 1995 Mach and Reynolds number effects on turbulent boundary layer behavior. In 33rd Aerospace Sciences Meeting and Exhibit. AIAA.CrossRefGoogle Scholar
Weinstein, L.M. 1993 Large-field high-brightness focusing schlieren system. AIAA J. 31 (7), 1250–1255.CrossRefGoogle Scholar
Weiss, J. 2019 A tutorial on the proper orthogonal decomposition. In AIAA Aviation 2019 Forum. AIAA.CrossRefGoogle Scholar
Wills, A.O., Awasthi, M., Doolan, C.J. & Moreau, D. 2019 Transient aspects of a shock-wave boundary layer interaction. In AIAA Aviation 2019. AIAA.CrossRefGoogle Scholar
Yang, R., Wang, Z.-g. & Wu, J.-p. 2020 Instability of an asymmetric supersonic planar wake. Acta Astronaut. 173, 86–90.CrossRefGoogle Scholar
Zhang, Z., McCreton, S.F., Awasthi, M., Wills, A.O., Moreau, D.J. & Doolan, C.J. 2021 The flow features of transverse jets in supersonic crossflow. Aerosp. Sci. Technol. 118, 107058.CrossRefGoogle Scholar