Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-27T18:35:53.333Z Has data issue: false hasContentIssue false
  • English
  • Français

Suppressing van der Waals driven rupture through shear

Published online by Cambridge University Press:  18 August 2010

M. J. DAVIS ,
M. B. GRATTON  and
S. H. DAVIS
M. J. DAVIS
Affiliation:
Department of Engineering Sciences and Applied Mathematics, McCormick School of Engineering and Applied Science, Northwestern University, Evanston, IL 60208, USA
M. B. GRATTON*
Affiliation:
Department of Engineering Sciences and Applied Mathematics, McCormick School of Engineering and Applied Science, Northwestern University, Evanston, IL 60208, USA
S. H. DAVIS
Affiliation:
Department of Engineering Sciences and Applied Mathematics, McCormick School of Engineering and Applied Science, Northwestern University, Evanston, IL 60208, USA
*
†Email address for correspondence: m-gratton@northwestern.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

An ultra-thin viscous film on a substrate is susceptible to rupture instabilities driven by van der Waals attractions. When a unidirectional ‘wind’ shear τ is applied to the free surface, the rupture instability in two dimensions is suppressed when τ exceeds a critical value τc and is replaced by a permanent finite-amplitude structure, an intermolecular-capillary wave, that travels at approximately the speed of the surface. For small amplitudes, the wave is governed by the Kuramoto–Sivashinsky equation. If three-dimensional disturbances are allowed, the shear is decoupled from disturbances perpendicular to the flow, and line rupture would occur. 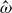In this case, replacing the unidirectional shear with a shear whose direction rotates with angular speed, , suppresses the rupture if τ ≳ 2τc. For the most dangerous wavenumber, τc ≈ 10−2 dyn cm−2 at 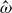≈ 1 rad s−1 for a film with physical properties similar to water at a thickness of 100 nm.

JFM classification

Instability: Instability Low-Reynolds-number flows: Lubrication theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 661 , 25 October 2010 , pp. 522 - 539
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, A. M., Brush, L. N. & Davis, S. H. 2010 Foam mechanics: spontaneous rupture of thinning liquid films with Plateau borders. J. Fluid Mech. doi:10.1017/s0022112010001527.CrossRefGoogle Scholar
Benney, D. J. 1966 Long waves in liquid film. J. Math. Phys. 45, 150–155.CrossRefGoogle Scholar
Bielarz, C. & Kalliadasis, S. 2003 Time-dependent free-surface thin film flows over topography. Phys. Fluids 15 (9), 2512–2524.CrossRefGoogle Scholar
Chang, H.-C. 1994 Wave evolution on a falling film. Annu. Rev. Fluid. Mech. 26, 103–136.CrossRefGoogle Scholar
Chang, H.-C., Demekhin, E. A., Kalaidin, E. & Ye, Y. 1996 Coarsening dynamics of falling-film solitary waves. Phys. Rev. E 54 (2), 1467–1477.CrossRefGoogle ScholarPubMed
Coons, J. E., Halley, P. J., McGlashan, S. A. & Tran-Cong, T. 2003 A review of drainage and spontaneous rupture in free standing thin films with tangentially immobile interfaces. Adv. Colloid Interface Sci. 105 (1–3), 3–62.CrossRefGoogle ScholarPubMed
Erneux, T. & Davis, S. H. 1993 Nonlinear rupture of free films. Phys. Fluids A 5 (5), 1117–1122.CrossRefGoogle Scholar
Gumerman, R. J. & Homsy, G. M. 1975 The stability of radially bounded thin films. Chem. Engng Commun. 2, 27–36.CrossRefGoogle Scholar
Holly, F. J. 1973 Formation and rupture of the tear film. Exp. Eye Res. 15 (5), 515–525.CrossRefGoogle ScholarPubMed
Ida, M. P. & Miksis, M. J. 1998 The dynamics of thin films. Part I. General theory. SIAM J. Appl. Maths 58 (2), 456–473.Google Scholar
Jacobs, K., Herminghaus, S. & Mecke, K. R. 1998 Thin liquid polymer films rupture via defects. Langmuir 14 (4), 965–969.CrossRefGoogle Scholar
Kalpathy, S. K., Francis, L. F. & Kumar, S. 2010 Shear-induced suppression of rupture in two-layer thin liquid films. J. Colloid Interface Sci. 348 (1), 271–279.CrossRefGoogle ScholarPubMed
King-Smith, E., Fink, B., Hill, R., Koelling, K. & Tiffany, J. 2004 The thickness of the tear film. Curr. Eye Res. 29 (4–5), 357–368.CrossRefGoogle ScholarPubMed
Lenz, R. D. & Kumar, S. 2007 Competitive displacement of thin liquid films on chemically patterned substrates. J. Fluid Mech. 571, 33–57.CrossRefGoogle Scholar
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931–980.CrossRefGoogle Scholar
Reiter, G. 1992 Dewetting of thin polymer films. Phys. Rev. Lett. 68 (1), 75–78.CrossRefGoogle ScholarPubMed
Ruckenstein, E. & Jain, R. K. 1974 Spontaneous rupture of thin liquid films. J. Chem. Soc. Faraday Trans. 2 70, 132.CrossRefGoogle Scholar
Schenk, O., Bollhoefer, M. & Roemer, R. 2008 On large-scale diagonalization techniques for the Anderson model of localization. SIAM Rev. 50, 91–112.CrossRefGoogle Scholar
Schenk, O., Waecher, A. & Hagermann, M. 2007 Matching-based preprocessing algorithms to the solution of saddle-point problems in large-scale nonconvex interior-point optimization. J. Comput. Optim. Appl. 36 (2–3), 321–341.CrossRefGoogle Scholar
Schulze, T. P. & Davis, S. H. 1995 Shear stabilization of morphological instability during directional solidification. J. Cryst. Growth 149, 253–265.CrossRefGoogle Scholar
Sharma, A. & Ruckenstein, E. 1986 Finite-amplitude instability of thin free and wetting films: predition of lifetimes. Langmuir 2, 480–494.CrossRefGoogle Scholar
Sheludko, A. 1967 Thin liquid films. Adv. Colloid Interface Sci. 1 (4), 391.CrossRefGoogle Scholar
Smyrlis, Y. S. & Papageorgiou, D. T. 1991 Chaos for infinite dimensional dynamical systems: the Kuramoto–Sivashinsky equation, a case study. Proc. Natl Acad. Sci. USA 88, 11129–11132.CrossRefGoogle ScholarPubMed
Teletzke, G. F., Davis, H. T. & Scriven, L. E. 1988 Wetting hydrodynamics. Rev. Phys. Appl. 23, 989–1007.CrossRefGoogle Scholar
Thiele, U. & Knobloch, E. 2004 Thin liquid films on a slightly inclined heated plate. Physica D 190, 213–248.CrossRefGoogle Scholar
Thiele, U., Neuffer, K., Bestehorn, M., Pomeau, Y. & Velarde, M. G. 2002 Sliding drops on an inclined plane. Colloids Surf. A 206, 87–104.CrossRefGoogle Scholar
Tseluiko, D. & Papageorgiou, D. T. 2006 a A global attracting set for nonlocal Kuramoto–Sivashinsky equations arising in interfacial electrohydrodynamics. Eur. J. Appl. Maths 17, 677–703.CrossRefGoogle Scholar
Tseluiko, D. & Papageorgiou, D. T. 2006 b Wave evolution on electrified falling films. J. Fluid Mech. 556, 361–386.CrossRefGoogle Scholar
Vaynblat, D., Lister, J. R. & Witelski, T. P. 2001 Rupture of thin viscous films by van der Waals forces: evolution and self-similarity. Phys. Fluids 13, 1130–1140.CrossRefGoogle Scholar
Vignes-Adler, M. 2002 Physico-Chemical Aspects of Forced Wetting, chap. 4, pp. 103–157. Springer.Google Scholar
Vrij, A. 1966 Possible mechanism for the spontaneous rupture of thin, free liquid films. Discuss. Faraday Soc. 43, 23.CrossRefGoogle Scholar
Williams, M. B. & Davis, S. H. 1982 Nonlinear theory of film rupture. J. Colloid Interface Sci. 90 (1), 220–228.CrossRefGoogle Scholar
Witelski, T. P. & Bernoff, A. J. 2000 Dynamics of three-dimensional thin film rupture. Physica D 147 (1–2), 155–176.CrossRefGoogle Scholar
Zhang, W. W. & Lister, J. R. 1999 Similarity solutions for van der Waals rupture of a thin film on a solid substrate. Phys. Fluids 11 (9), 2454–2462.CrossRefGoogle Scholar