Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T05:43:44.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Surface waves along liquid cylinders. Part 2. Varicose, sinuous, sloshing and nonlinear waves

Published online by Cambridge University Press:  27 July 2021

Gabriel Le Doudic Open the ORCID record for Gabriel Le Doudic [Opens in a new window] ,
Stéphane Perrard Open the ORCID record for Stéphane Perrard [Opens in a new window]  and
Chi-Tuong Pham Open the ORCID record for Chi-Tuong Pham [Opens in a new window]
Gabriel Le Doudic
Affiliation:
Laboratoire Matière et Systèmes Complexes, Université de Paris, CNRS, 10 rue Alice Domon et Léonie Duquet, 75013Paris, France
Stéphane Perrard
Affiliation:
Laboratoire de Physique de l’École normale supérieure, École normale supérieure, Université PSL, CNRS, Sorbonne Université, Université de Paris, 24 rue Lhomond, 75005Paris, France
Chi-Tuong Pham*
Affiliation:
Laboratoire Interdisciplinaire des Sciences du Numérique, Université Paris-Saclay, CNRS, Bâtiment 507, rue John von Neumann, 91400Orsay, France
*
†Email address for correspondence: pham@limsi.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

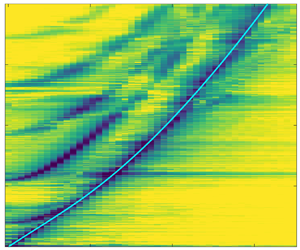
Gravity–capillary waves propagating along extended liquid cylinders in the inviscid limit are studied in the context of experiments on sessile cylinders deposited upon superhydrophobic substrates, with tunable geometries. In Part 1 of this work (Pham et al., J. Fluid Mech., vol. 891, 2020, A5), we characterised the non-dispersive regime of the varicose waves. In this second part, we characterise the varicose waves in the dispersive regime, as well as the sinuous and the sloshing modes. We numerically study the shape function of the system (the counterpart of the standard $\tanh$ function of the dispersion relation of a gravity–capillary wave in a rectangular channel) and the cutoff frequencies of the sloshing modes, and show how they depend on the geometry of the substrate. A reduced-gravity effect is evidenced and the transition between a capillary- and a gravity-dominated regime is expressed in terms of an effective Bond number and an effective surface tension. Semiquantitative agreement is found between the theoretical computations and the experiments. As a consequence of these results, resorting to the inviscid section-averaged Saint-Venant equations, we propose a Korteweg–de Vries equation with adapted coefficients that governs the propagation of localised nonlinear waves. We relate these results to the propagation of depression solitons observed in our experimental set-up and along Leidenfrost cylinders levitating above a hot substrate (Perrard et al., Phys. Rev. E, vol. 92, 2015, 011002(R)). We extend our derivation of the Korteweg–de Vries equation to solitary-like waves propagating along Plateau borders in soap films, evidenced by Argentina et al. (J. Fluid. Mech., vol. 765, 2015, pp. 1–16).

JFM classification

Waves/Free-surface Flows: Solitary waves Drops and Bubbles: Drops
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 923 , 25 September 2021 , A13
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Argentina, M., Cohen, A., Bouret, Y., Fraysse, N. & Raufaste, C. 2015 One-dimensional capillary jumps. J. Fluid Mech. 765, 1–16.CrossRefGoogle Scholar
Bostwick, J.B. & Steen, P.H. 2018 Static rivulet instabilities: varicose and sinuous modes. J. Fluid Mech. 837, 819–838.CrossRefGoogle Scholar
Bouret, Y., Cohen, A., Fraysse, N., Argentina, M. & Raufaste, C. 2016 Solitary-like waves in a liquid foam microchannel. Phys. Rev. Fluids 1, 043902.CrossRefGoogle Scholar
Craik, A.D.D. 2004 The origins of water wave theory. Annu. Rev. Fluid Mech. 36, 1–28.CrossRefGoogle Scholar
Craik, A.D.D. 2005 George Gabriel Stokes on water wave theory. Annu. Rev. Fluid Mech. 37, 23–42.CrossRefGoogle Scholar
Davis, S.H. 1980 Moving contact lines and rivulet instabilities. Part 1. The static rivulet. J. Fluid Mech. 98, 225–242.CrossRefGoogle Scholar
Decoene, A., Bonaventura, L., Miglio, E. & Saleri, F. 2009 Asymptotic derivation of the section-averaged shallow water equations. Math. Models Meth. Appl. Sci. 19, 387–417.CrossRefGoogle Scholar
Earnshaw, R.. S. 1860 On the mathematical theory of sound. Phil. Trans. R. Soc. 150, 133–148.Google Scholar
Engwirda, D. 2014 Locally optimized Delaunay-refinement and optimisation-based mesh generation. PhD thesis, The University of Sydney. Available at: https://github.com/dengwirda/mesh2d.Google Scholar
Falcon, É., Laroche, C. & Fauve, S. 2002 Observation of depression solitary surface waves on a thin fluid layer. Phys. Rev. Lett. 89, 204501.CrossRefGoogle ScholarPubMed
Forel, F.A. 1904 Le Léman: Monographie Limnologique, 2nd edn. F. Rouge & Cie.Google Scholar
Groves, M.D. 1994 Hamiltonian long-wave theory for water waves in a channel. Q. J. Mech. Appl. Maths 47, 367–404.CrossRefGoogle Scholar
Gupta, R., Vaikuntanathan, V. & Siakumar, S. 2016 Superhydrophobic qualities of an aluminum surface coated with hydrophobic solution NeverWet. Colloids Surf. A 500, 45–53.CrossRefGoogle Scholar
Korteweg, D.J. & de Vries, G. 1895 On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Phil. Mag. J. Sci. 39, 422–443.CrossRefGoogle Scholar
Kosgodagan Acharige, A., Elias, F. & Derec, C. 2014 Soap film vibration: origin of the dissipation. Soft Matt. 10, 8341–8348.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Langbein, D. 1990 The shape and stability of liquid menisci at solid edges. J. Fluid Mech. 213, 251–265.CrossRefGoogle Scholar
McIver, M. & McIver, P. 1993 Sloshing frequencies of longitudinal modes for a liquid contained in a trough. J. Fluid Mech. 252, 525–541.CrossRefGoogle Scholar
Perrard, S., Deike, L., Duchêne, C. & Pham, C.-T. 2015 Capillary solitons on a levitated medium. Phys. Rev. E 92, 011002(R).CrossRefGoogle ScholarPubMed
Pham, C.-T., Perrard, S. & Le Doudic, G. 2020 Surface waves along liquid cylinders. Part 1. Stabilising effect of gravity on the Plateau–Rayleigh instability. J. Fluid Mech. 891, A5.CrossRefGoogle Scholar
Plateau, J. 1849 Recherches expérimentales et théoriques sur les figures d'une masse liquide sans pesanteur. Mem. Acad. R. Sci. Lett. Belg. 23, 1–150.Google Scholar
Rayleigh, Lord 1878 On the instability of jets. Proc. Lond. Math. Soc. 10, 4–13.CrossRefGoogle Scholar
Roy, V. & Schwartz, L.W. 1999 On the stability of liquid ridges. J. Fluid Mech. 291, 293–318.CrossRefGoogle Scholar
Russell, J.S. 1844 Report on Waves. Report of the 14th Meeting of the British Association for the Advancement of Science, pp. 311–390. John Murray.Google Scholar
Saint-Venant, A.J.C.B. 1871 Théorie du mouvement non permanent des eaux, avec application aux crues des rivières et à l'introduction de marées dans leurs lits. C. R. Acad. Sci. 73, 147–154 and 237–240.Google Scholar
Savart, F. 1833 Mémoire sur la constitution des veines liquides lancées par des orifices circulaires en mince paroi. Ann. Chim. Phys. 53, 337–386.Google Scholar
Segel, L.A. & Handelman, G.H. 1987 Mathematics Applied to Continuum Mechanics. Dover.Google Scholar
Sekimoto, K., Oguma, R. & Kawasaki, K. 1987 Morphological stability analysis of partial wetting. Ann. Phys. 176, 359–392.CrossRefGoogle Scholar
Speth, R.L. & Lauga, E. 2009 Capillary instability on a hydrophilic stripe. New J. Phys. 11, 075024.CrossRefGoogle Scholar
Wehausen, J.V. & Laitone, E.V. 1960 Surface Waves. Springer.CrossRefGoogle Scholar
Whitham, G.B. 1999 Linear and Nonlinear Waves. John Wiley.CrossRefGoogle Scholar
Yang, L. & Homsy, G.M. 2007 Capillary instabilities of liquid films inside a wedge. Phys. Fluids 19, 044101.CrossRefGoogle Scholar

Le Doudic at al. Supplementary Movie

Generated by a micro-pipette at one tip of the drop, a liquid jet induces a strong deformation of the drop. Waves propagate ahead of a solitary depression wave and the latter travels at a speed lower than the propagation speed of the long-wavelength waves. This depression wave corresponds to a negative-amplitude Korteweg--de Vries soliton.

Download Le Doudic at al. Supplementary Movie(Video)
Video 12.5 MB