Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2025-01-01T09:12:57.953Z Has data issue: false hasContentIssue false
  • English
  • Français

A suspension of conducting particles in a magnetic field – the particle stress

Published online by Cambridge University Press:  02 September 2020

V. Kumaran Open the ORCID record for V. Kumaran [Opens in a new window]
V. Kumaran*
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore560 012, India
*
†Email address for correspondence: kumaran@iisc.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

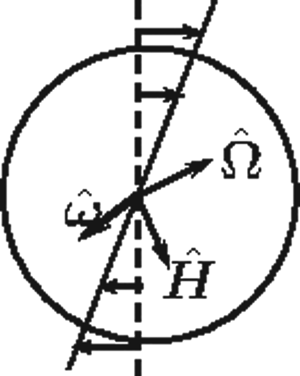
When a suspension of conducting particles is subjected to a shear flow, there is particle rotation due to the fluid vorticity. A conductor rotating in a uniform magnetic field experiences a torque due to eddy currents both parallel and perpendicular to the direction of rotation. Eddy currents induce a magnetic moment in a conducting particle, which disturbs the magnetic field around the particle. The effect of the Maxwell stress due to the magnetic field disturbance on the rheology of a dilute suspension is calculated in a manner similar to the Einstein viscosity for a suspension of rigid particles. The expression for the stress tensor contains three symmetric stress coefficients, and two normal stress coefficients, in addition to the three antisymmetric stress coefficients calculated in Kumaran (J. Fluid Mech., vol. 871, 2019, pp. 139–185). The stress coefficients depend on the relative orientation of the vorticity and magnetic field and two dimensionless parameters, $\beta$, the product of the vorticity and current relaxation time, and $\Sigma$, the ratio of the magnetic and hydrodynamic torques. In the ‘linear’ approximation, where only terms linear in the particle magnetic moment are retained, the particle stress depends on two dimensionless functions. For the physically important limit $\beta \ll 1$, as well as the limit $\beta \gg 1$ and $\Sigma \gg 1$, these two functions are independent of the vorticity, and depend only on the magnetic field and material properties.

JFM classification

Complex Fluids: Suspensions Non-Newtonian Flows: Rheology MHD and Electrohydrodynamics: Magnetic fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 901 , 25 October 2020 , A36
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Almog, Y. & Frankel, I. 1995 The motion of axisymmetric dipolar particles in a homogeneous shear flow. J. Fluid Mech. 289, 243–261.10.1017/S0022112095001327CrossRefGoogle Scholar
Anupama, A. V., Kumaran, V. & Sahoo, B. 2018 Magnetorheological fluids containing rod-shaped lithium-zinc ferrite particles: the steady-state shear response. Soft Matt. 14, 5407–5419.10.1039/C8SM00807HCrossRefGoogle ScholarPubMed
Batchelor, G. K. 1970 The stress in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.10.1017/S0022112070000745CrossRefGoogle Scholar
Bolcato, R., Etay, J., Fautrelle, Y. & Moffatt, H. K. 1993 Electromagnetic billiards. Phys. Fluids A 5, 1852–1853.10.1063/1.858809CrossRefGoogle Scholar
Brown, M. A., Duyckaerts, N., Redondo, A. B., Jordan, I., Nolting, F., Kleibert, A., Ammann, M., Worner, H. J., van Bokhoven, J. A. & Abbas, Z. 2013 Effect of surface charge density on the affinity of oxide nanoparticles for the vapor-water interface. Langmuir 29 (16), 5023–5029.10.1021/la4005054CrossRefGoogle ScholarPubMed
Campos, A. F. C., de Medeiros, W. C., Aquino, R. & Depeyrot, J. 2017 Surface charge density determination in water based magnetic colloids: a comparative study. J. Mater. Res. 20, 1729–1734.10.1590/1980-5373-mr-2017-0649CrossRefGoogle Scholar
Chaves, A., Zahn, M. & Rinaldi, C. 2008 Spin-up flow of ferrofluids: asymptotoic theory and experimental measurements. Phys. Fluids 20, 053102.10.1063/1.2907221CrossRefGoogle Scholar
Condiff, D. W. & Dahler, J. S. 1964 Fluid mechanical aspects of antisymmetric stress. Phys. Fluids 7, 842–854.CrossRefGoogle Scholar
Dahler, J. S. & Scriven, L. E. 1963 Theory of structured continua. I. General consideration of angular momentum and polarization. Proc. R. Soc. Lond. A 275, 504–527.Google Scholar
Feng, S., Graham, A. L., Abbott, J. R. & Brenner, H. 2006 Antisymmetric stresses in suspensions: vortex viscosity and energy dissipation. J. Fluid Mech. 563, 97–122.10.1017/S0022112006001066CrossRefGoogle Scholar
Fernandez-Barbero, A., Cabrerizo-Vilchez, M., Martinez-Garcia, R. & Hidalgo-Alvarez, R. 1996 Effect of the particle surface charge density on the colloidal aggregation mechanism. Phys. Rev. E 53, 4981–4989.CrossRefGoogle ScholarPubMed
Goldstein, H. 1989 Clasical Mechanics. Narosa Publishing House, chap. 4.Google Scholar
Halverson, R. P. & Cohen, H. 1964 Torque on a spinning hollow sphere in a uniform magnetic field. IEEE Trans. Aerosp. Navig. Electron. ANE-11, 118–122.CrossRefGoogle Scholar
Hsu, M. F., Dufresne, E. R. & Weitz, D. A. 2005 Charge stabilization in nonpolar solvents. Langmuir 21, 4881–4887.10.1021/la046751mCrossRefGoogle ScholarPubMed
Jansons, K. M. 1983 Determination of the constitutive equations for a magnetic fluid. J. Fluid Mech. 137, 187–216.CrossRefGoogle Scholar
Klingenberg, D. J. 2001 Magnetorheology: applications and challenges. AIChE J. 47, 246–249.CrossRefGoogle Scholar
Klingenberg, D. J. & Zukoski, C. F. 1990 Studies on the steady-shear behavior of electrorheological suspensions. Langmuir 6, 15–24.CrossRefGoogle Scholar
Kumaran, V. 2019 Rheology of a suspension of conducting particles in a magnetic field. J. Fluid Mech. 871, 139–185.CrossRefGoogle Scholar
Kumaran, V. 2020 Bifurcations in the dynamics of a dipolar spheroid in a shear flow subjected to an external field. Phys. Rev. Fluids 5, 033701.CrossRefGoogle Scholar
Kuzhir, P., Lopez-Lopez, M. T. & Bossis, G. 2009 Magnetorheology of fiber suspensions. II. Theory. J. Rheol. 53, 127–151.CrossRefGoogle Scholar
Landau, L. D., Lifshitz, E. M. & Pitaevskii, L. P. 2014 Electrodynamics of Continuous Media. Butterworth-Heinemann.Google Scholar
Lopez-Lopez, M. T., Kuzhir, P. & Bossis, G. 2009 Magnetorheology of fiber suspensions. I. Experimental. J. Rheol. 53, 115–126.CrossRefGoogle Scholar
Mindlin, R. & Tiersten, H. 1962 Effects of couple-stresses in linear elasticity. Arch. Rat. Mech. Anal. 11, 415–448.10.1007/BF00253946CrossRefGoogle Scholar
Moffat, H. K. 1990 On the behaviour of a suspension of conducting particles subjected to a time-periodic magnetic field. J. Fluid Mech. 218, 509–529.CrossRefGoogle Scholar
Moskowitz, R. & Rosensweig, R. E. 1967 Nonmechanical torque-driven flow of a ferromagnetic fluid by an electromagnetic field. Appl. Phys. Lett. 11, 301–303.10.1063/1.1754952CrossRefGoogle Scholar
Rinaldi, C. & Zahn, M. 2002 Effects of spin viscosity on ferrofluid flow profiles in alternating and rotating magnetic fields. Phys. Fluids 14, 2847.10.1063/1.1485762CrossRefGoogle Scholar
Rosensweig, R. E. 2000 Continuum equations for magnetic and dielectric fluids with internal rotations. J. Chem. Phys. 121, 1228.10.1063/1.1755660CrossRefGoogle Scholar
Sherman, S. G., Becnel, A. C. & Wereley, N. M. 2015 Relating mason number to bingham number in magnetorheological fluids. J. Magn. Magn. Mater. 380, 98–104.10.1016/j.jmmm.2014.11.010CrossRefGoogle Scholar
Sobecki, C. A., Zhang, J., Zhang, Y. & Wang, C. 2018 Dynamics of paramagnetic and ferromagnetic ellipsoidal particles in shear flow under a uniform magnetic field. Phys. Rev. Fluids 3, 084201.CrossRefGoogle Scholar
Stokes, V. K. 1966 Couple stresses in fluids. Phys. Fluids 9, 1709–1715.10.1063/1.1761925CrossRefGoogle Scholar
Truesdell, C. & Toupin, R. A. 1960 The classical field theories. In Handbuch der Physik (ed. Flugge, S.), pp. 545–609. Springer.Google Scholar
Vagberg, D. & Tighe, B. P. 2017 On the apparent yield stress in non-Brownian magnetorheological fluids. Soft Matt. 13, 7207–7221.CrossRefGoogle ScholarPubMed
de Vicente, J., Klingenberg, D. J. & Hidalgo-Alvarez, R. 2011 Magnetorheological fluids: a review. Soft Matt. 7, 3701–3710.CrossRefGoogle Scholar
Waggett, F., Shafiq, M. D. & Bartlett, P. 2018 Failure of Debye-Hückel screening in low-charge colloidal suspensions. Colloids Interfaces 2, 51.10.3390/colloids2040051CrossRefGoogle Scholar
Wang, W. & Prosperetti, A. 2001 Flow of spatially non-uniform suspensions. Part III: closure relations for porous media and spinning particles. Intl J. Multiphase Flow 27, 1627–1653.CrossRefGoogle Scholar
Zaitsev, V. M. & Shliomis, M. I. 1969 Entrainment of ferromagnetic suspension by a rotating field. J. Appl. Mech. Tech. Phys. 10, 696–700.10.1007/BF00907424CrossRefGoogle Scholar